MATH36031 Project 2 狐狸追兔微分方程模型详解(Matlab源码)
23.11.24 版
纯知识分享,讲解题目
文末有源码和report 仅供参考
来自UCM 曼大MATH36031 solving by computer Project 2
原题链接
题目描述
初始配置如图1所示,
狐狸在原点O(0, 0)开始追逐兔子,而兔子试图逃离捕食者并朝着自己的洞穴移动。
兔子最初位于(0, 800)处。有一个圆形围栏,在(0, 300)处有一个开口G。兔子沿着半径为800的圆形路径以速度
s
r
s_r
sr向着自己的洞穴移动。
兔子的洞穴位于800(-sin(π/3),cos(π/3))处。
狐狸的路径最初直指G点,并以速度
s
f
s_f
sf移动。
在到达G点后,狐狸接下来尝试捕捉兔子的路径取决于它是否被直线围栏A和E之间的直线挡住了对兔子的视线,具体情况如下:
- 如果狐狸通过开口G后能看到兔子,狐狸的进攻路径直指兔子(狐狸速度向量的方向正好是从狐狸指向兔子的方向);
- 如果兔子的视线被一条无法穿透的直线围栏AE挡住,参见图1,则狐狸直接朝着角点A奔跑。围栏AE的坐标为A(−350, 620)和E(−500, 350)。一旦狐狸再次能看到兔子,其进攻路径将直指兔子。

问题 1:恒定速度。假设狐狸和兔子分别以恒定速度运行,即 s f = s f 0 = 17 s_f = s_{f_0} = 17 sf=sf0=17米/秒和 s r = s r 0 = 12 s_r = s_{r_0} = 12 sr=sr0=12米/秒,确定兔子是否能在到达洞穴之前被狐狸捕获。如果它们之间的距离小于或等于0.1米,则认为兔子被狐狸捕获。
问题 2:递减速度。考虑一个更现实的情景,即饥饿的狐狸遇到疲惫的兔子。因为狐狸和兔子都不处于最佳状态,根据它们相遇并开始奔跑后所行驶的距离,它们的追逐逃跑速度随时间递减。更准确地说,它们在时间t时的速度由以下公式给出:
s f ( t ) = s f 0 e − μ f d f ( t ) s_f(t) = s_{f_0}e^{-\mu_f d_f(t)} sf(t)=sf0e−μfdf(t)
s r ( t ) = s r 0 e − μ r d r ( t ) s_r(t) = s_{r_0}e^{-\mu_r d_r(t)} sr(t)=sr0e−μrdr(t)
其中 s f 0 = 17 s_{f_0} = 17 sf0=17米/秒和 s r 0 = 17 s_{r_0} = 17 sr0=17米/秒是与上述相同的初始速度, µ f = 0.0002 µ_f = 0.0002 µf=0.0002米^(-1)和 µ r = 0.0008 µ_r = 0.0008 µr=0.0008米^(-1)是速度递减的速率, d f ( t ) d_f(t) df(t)和 d r ( t ) d_r(t) dr(t)分别是到达时间t(> 0)时它们所行驶的距离。确定兔子是否能在到达洞穴之前被狐狸捕获。(可以假设这种速度递减从t = 0开始。)
解题思路
整体而言是将整个追逐过程分为两部分。
第一部分为狐狸到达G点,兔子沿着圆弧走。
第二部分为狐狸追逐兔子,在此期间判断AE的阻挡并且计算狐狸的微分方程。
两部分可以分别求解。
模型建立
关于追逐问题的微分方程模型,可以先参考matlab微分方程求解导弹追击问题这篇文章,文章的一部分思路来源与此。
我们设置狐狸
(
x
(
t
)
,
y
(
t
)
)
(x(t),y(t))
(x(t),y(t))和兔子
(
P
(
t
)
,
Q
(
t
)
)
(P(t),Q(t))
(P(t),Q(t)),x和y方向速度分别如下,cos和sin 后面表示的是他的方向角度
d x d t = d x f d t = s f ( t ) ⋅ cos ( f a n g l e ) \frac{dx}{dt} = \frac{dx_f}{dt} = s_f(t)\cdot \cos(f_{angle}) dtdx=dtdxf=sf(t)⋅cos(fangle)
d y d t = d y f d t = s f ( r ) ⋅ sin ( f a n g l e ) \frac{dy}{dt} = \frac{dy_f}{dt} = s_f(r)\cdot \sin(f_{angle}) dtdy=dtdyf=sf(r)⋅sin(fangle)
d P d t = d x r d t = s r ( t ) ⋅ cos ( r a n g l e ) \frac{dP}{dt} = \frac{dx_r}{dt} = s_r(t)\cdot \cos(r_{angle}) dtdP=dtdxr=sr(t)⋅cos(rangle)
d
Q
d
t
=
d
y
r
d
t
=
s
r
(
t
)
⋅
sin
(
r
a
n
g
l
e
)
\frac{dQ}{dt} = \frac{dy_r}{dt} = s_r(t) \cdot \sin(r_{angle})
dtdQ=dtdyr=sr(t)⋅sin(rangle)

根据如上公式 因为狐狸的速度向量是跟着兔子走的,所以我们根据微分方程得出fox速度轨迹
d
x
f
d
t
\frac{dx_f}{dt}
dtdxf,
d
y
f
d
t
\frac{dy_f}{dt}
dtdyf,具体代码如下
fox_distance_squared = (y(1) - y(3))^2 + (y(2) - y(4))^2;
fox_distance = sqrt(fox_distance_squared);
dy(1) = vf / fox_distance * (y(3) - y(1)); % vf 这里在Q1为17 m/s
dy(2) = vf / fox_distance * (y(4) - y(2));
而兔子的轨迹为圆弧已知,初始速度乘以对应方向角即可。具体代码如下
d x r d t = − s r 0 ⋅ sin θ d y r d t = s r 0 ⋅ cos θ \frac{dx_r}{dt} = -s_{r_0} \cdot \sin\theta \\ \frac{dy_r}{dt} = s_{r_0} \cdot \cos\theta dtdxr=−sr0⋅sinθdtdyr=sr0⋅cosθ
theta = atan2(y(4), y(3));
dy(3) = -vr * sin(theta); vr 这里在Q1为 12 m/s
dy(4) = vr * cos(theta);
目前我们把fox和rabbit的速度微分方程都求出来了,现在考虑fox的AE阻挡问题,当什么数学条件的时候,fox是被阻挡的?
由题意显然得出,当狐狸处于AE线段下方时,fox才能被阻挡。
这里我们使用polyxpoly 函数去计算AE与fox和rabbit之间的连线,若有交点,则被阻挡。
此时fox 的速度微分方程发生改变,速度指向A点,代码如下
fox_distance_to_A_squared = (y(1) - A(1))^2 + (y(2) - A(2))^2;
fox_distance_to_A = sqrt(fox_distance_to_A_squared);
dy(1) = vf / fox_distance_to_A * (A(1) - y(1));
dy(2) = vf / fox_distance_to_A * (A(2) - y(2));
以上,再继续使用ODE45 即可求解Q1
% ODE
tspan = [0, 100];
y0 = [0, 300, x_r, y_r];
options = odeset('RelTol', 1e-6, 'AbsTol', 1e-6, 'MaxStep', 0.1);
[t1, y1] = ode45(@(t, y) diff_equal(t, y, sf, sr), tspan, y0, options);
Q2
对于Q2 来说, 速度不再为固定值,而是为速度随距离变化的函数。
对于这个距离的计算,我们这里采取微分的形式,每一次步长点与点之间的间距求解出来之后去求和。
muf = 0.0002; % 狐狸速度减小率
mur = 0.0008; % 兔子速度减小率
if t > 0
% 计算狐狸和兔子当前时间步长的位移
fox_displacement = sqrt(square_contract(y(1),y(2),prev_fox_position(1),prev_fox_position(2)));
rabbit_displacement = sqrt(square_contract(y(3),y(4),prev_rabbit_position(1),prev_rabbit_position(2)));
% 累积狐狸和兔子的行走距离
fox_distance = fox_distance + fox_displacement;
rabbit_distance = rabbit_distance + rabbit_displacement;
else
fox_distance = 0;
rabbit_distance = 0;
end
prev_fox_position = [y(1), y(2)];
prev_rabbit_position = [y(3), y(4)];
% dy1 dy2 fox
% dy3 dy4 rabbit
% fox
vf = vf * exp(-muf * fox_distance);
vr = vr * exp(-mur * rabbit_distance);
然后剩余的Q1一样,只不过是将速度的固定值换为距离值。
最后我们Q1Q2的fox和rabbit的轨迹如图
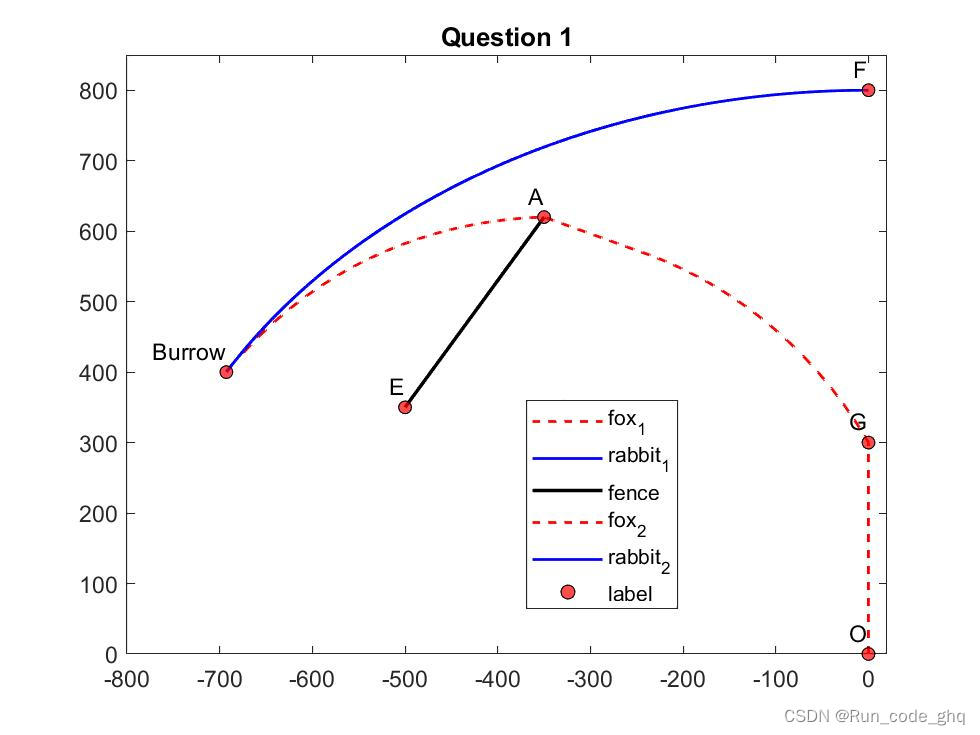
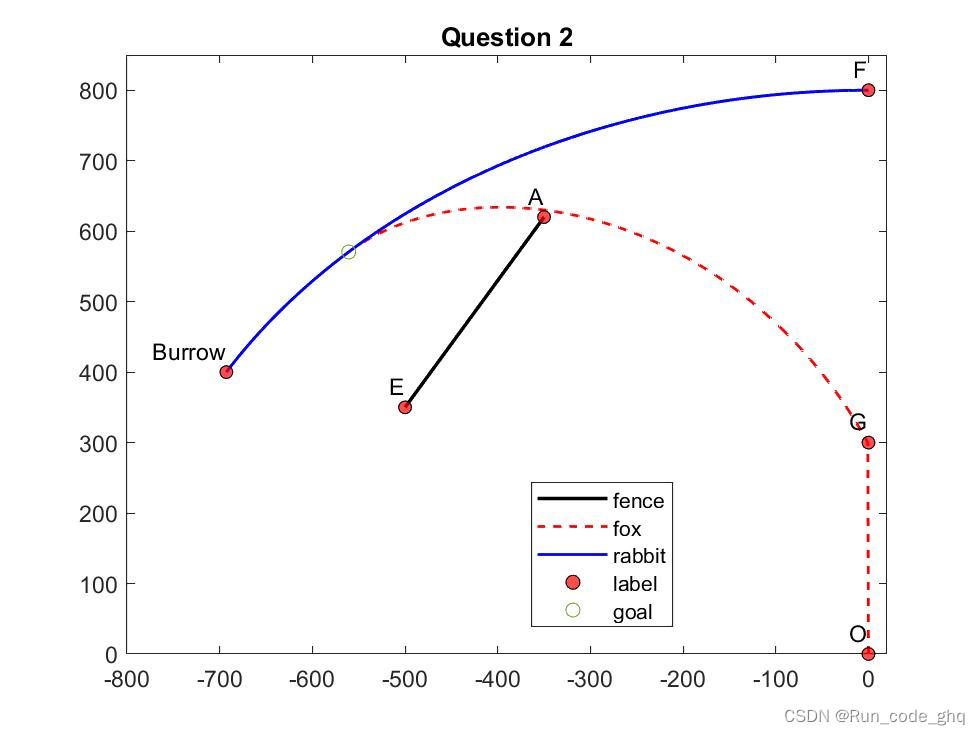
The original link:link code= lvgg
code and report here: link
优惠码:FZNVEM
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








