文章目录
第3章 有穷自动机和正规表达式
有穷自动机
DFA
确定的有穷自动机(DFA)是个五元组: M = ( Q , Σ , δ , q 0 , F ) M=(Q,\Sigma,\delta,q_0,F) M=(Q,Σ,δ,q0,F) ,其中:
- Q Q Q 是有穷状态集
- Σ \Sigma Σ 是有穷的输入字母表
- δ \delta δ 是转移函数, δ : Q × Σ → Q \delta:\, Q\times\Sigma\to Q δ:Q×Σ→Q
- q 0 ∈ Q q_0\,\in\, Q q0∈Q ,是初始状态
- F ⊆ Q F\,\subseteq\,Q F⊆Q ,是终结状态集
转移函数定义拓展:
{
δ
^
(
q
,
ε
)
=
q
δ
^
(
q
,
w
a
)
=
δ
(
δ
^
(
q
,
w
)
,
a
)
\left \{ \begin{array}{ll} \hat{\delta}(q,\varepsilon)=q\\ \hat{\delta}(q,wa)=\delta(\hat{\delta}(q,w),a) \end{array} \right.
{δ^(q,ε)=qδ^(q,wa)=δ(δ^(q,w),a)
其中
w
w
w 是字符串,
w
∈
Σ
∗
w\in{\Sigma}^{\ast}
w∈Σ∗
NFA
定义与 DFA 类似,不同之处在于转移函数 δ : Q × Σ → 2 Q \delta:\, Q\times\Sigma\to 2^Q δ:Q×Σ→2Q ,即下一状态是个集合;只要有一条分支到达 F F F 就算接受
转移函数定义拓展:
{
δ
^
(
q
,
ε
)
=
{
q
}
δ
^
(
q
,
w
a
)
=
{
p
∣
p
∈
δ
(
r
,
a
)
,
r
∈
δ
^
(
q
,
w
)
}
\left \{ \begin{array}{ll} \hat{\delta}(q,\varepsilon)=\{q\}\\ \hat{\delta}(q,wa)=\{p|p\,\in\,\delta(r,a)\, ,r\,\in\,\hat{\delta}(q,w)\} \end{array} \right.
{δ^(q,ε)={q}δ^(q,wa)={p∣p∈δ(r,a),r∈δ^(q,w)}
其中
w
w
w 是字符串,
w
∈
Σ
∗
w\in{\Sigma}^{\ast}
w∈Σ∗
ε \varepsilon ε-NFA
定义与 NFA 类似,不同之处在于转移函数还可以接受空串/空字符 ε \varepsilon ε
转移函数定义拓展:
{
δ
^
(
q
,
ε
)
=
ε
−
C
L
O
S
U
R
E
(
q
)
δ
^
(
q
,
w
a
)
=
ε
−
C
L
O
S
U
R
E
(
P
)
,
P
=
∪
r
∈
δ
^
(
q
,
w
)
δ
(
r
,
a
)
\left \{ \begin{array}{ll} \hat{\delta}(q,\varepsilon)={\varepsilon}-CLOSURE(q)\\ \hat{\delta}(q,wa)={\varepsilon}-CLOSURE(P),{\,}P={\cup}_{r\,\in\,\hat{\delta}(q,w)}{\delta}(r,a) \end{array} \right.
{δ^(q,ε)=ε−CLOSURE(q)δ^(q,wa)=ε−CLOSURE(P),P=∪r∈δ^(q,w)δ(r,a)
其中
ε
−
C
L
O
S
U
R
E
(
q
)
\varepsilon -CLOSURE(q)
ε−CLOSURE(q) 定义为:
- q q q 在 ε − C L O S U R E ( q ) \varepsilon -CLOSURE(q) ε−CLOSURE(q) 中
- 若 p p p 在 ε − C L O S U R E ( q ) \varepsilon -CLOSURE(q) ε−CLOSURE(q) 中,则 δ ( p , ε ) \delta(p,{\varepsilon}) δ(p,ε) 也在 ε − C L O S U R E ( q ) \varepsilon -CLOSURE(q) ε−CLOSURE(q) 中
- 重复以上步骤,直至 ε − C L O S U R E ( q ) \varepsilon -CLOSURE(q) ε−CLOSURE(q) 不再增加为止
(可以理解成从状态 q q q 出发,仅通过接受 ε \varepsilon ε 可以到达的状态集)
结构图

NFA → \to → DFA
算法描述
算法:将状态的集合看作状态(状态会发生改变);从起始状态开始,逐一尝试字母表中每个字母,获得下一状态;对于新增加的状态,重复上述过程,直到不再有新的状态产生;
例题
例:将如图所示的 NFA 转化为相应的 DFA,转移函数:
δ ( q 0 , 0 ) = { q 0 , q 3 } \delta(q_0,0)=\{q_0,q_3\} δ(q0,0)={q0,q3} δ ( q 0 , 1 ) = { q 0 , q 1 } \delta(q_0,1)=\{q_0,q_1\} δ(q0,1)={q0,q1}
δ ( q 1 , 0 ) = ∅ \delta(q_1,0)=\varnothing δ(q1,0)=∅ δ ( q 1 , 1 ) = { q 2 } \delta(q_1,1)=\{q_2\} δ(q1,1)={q2}
δ ( q 2 , 0 ) = { q 2 } \delta(q_2,0)=\{q_2\} δ(q2,0)={q2} δ ( q 2 , 1 ) = { q 2 } \delta(q_2,1)=\{q_2\} δ(q2,1)={q2}
δ ( q 3 , 0 ) = { q 4 } \delta(q_3,0)=\{q_4\} δ(q3,0)={q4} δ ( q 3 , 1 ) = ∅ \delta(q_3,1)=\varnothing δ(q3,1)=∅
δ ( q 4 , 0 ) = { q 4 } \delta(q_4,0)=\{q_4\} δ(q4,0)={q4} δ ( q 4 , 1 ) = { q 4 } \delta(q_4,1)=\{q_4\} δ(q4,1)={q4}
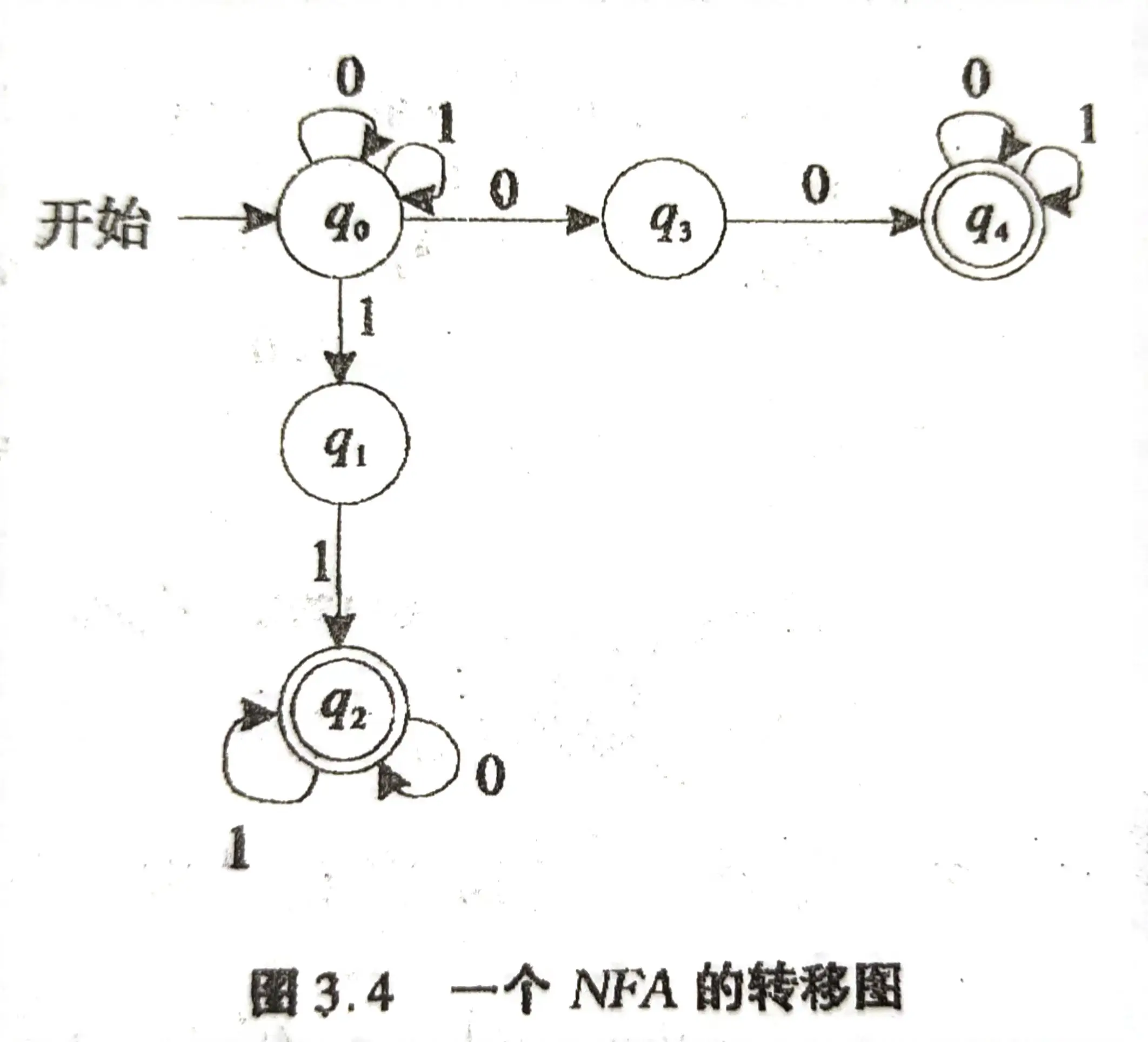
过程:


ε \varepsilon ε-NFA → \to → NFA
算法描述
算法:
① 状态并不改变,转移路径去除了接受 ε \varepsilon ε 的路径;
② 增加了另外许多路径,增加规则如下:
- 对于 δ ( q , a ) = P \delta(q,a)=P δ(q,a)=P ,则增加路径 q → a ε − C L O S U R E ( P ) q\overset{a}{\to}{\varepsilon}-CLOSURE(P) q→aε−CLOSURE(P) ;
- 对于 Q ⊆ ε − C L O S U R E ( q ) Q\subseteq{\varepsilon}-CLOSURE(q) Q⊆ε−CLOSURE(q) 且 Q → a P Q\overset{a}{\to}P Q→aP ,增加路径 q → a P q\overset{a}{\to}P q→aP ;
(即需要增加:① 能够通过 q q q 的闭包到达的状态;② q q q 能够到达状态的闭包)
③ 处理终结状态:
F
′
=
{
F
∪
{
q
0
}
,
i
f
ε
−
C
L
O
S
U
R
E
(
q
0
)
∩
F
≠
∅
F
,
e
l
s
e
F'=\left \{ \begin{array}{ll} F{\cup}\{q_0\},{\quad}if{\,}{\,}{\,}{\,}{\varepsilon}-CLOSURE(q_0){\cap}F{\not=}{\varnothing}\\ F,{\quad}{\quad}{\quad}{\,}{\,}{\,}else \end{array} \right.
F′={F∪{q0},ifε−CLOSURE(q0)∩F=∅F,else
(就是说,如果原来从起始状态出发,不接受任何字符就可以到达终结状态,那么起始状态事实上也是终结状态)
例题
例:将如图所示的 ε \varepsilon ε-NFA 转化为 NFA:
| 转化前 | 转化后 |
|---|---|
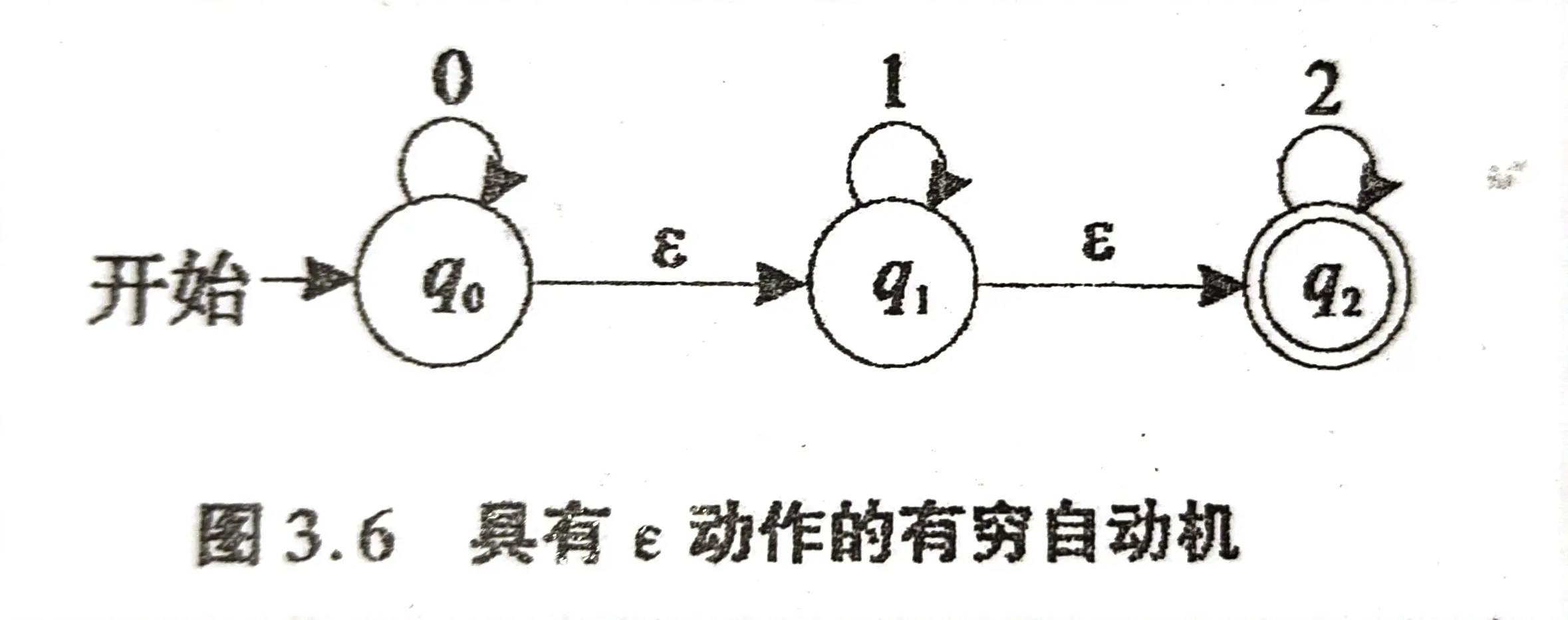 | 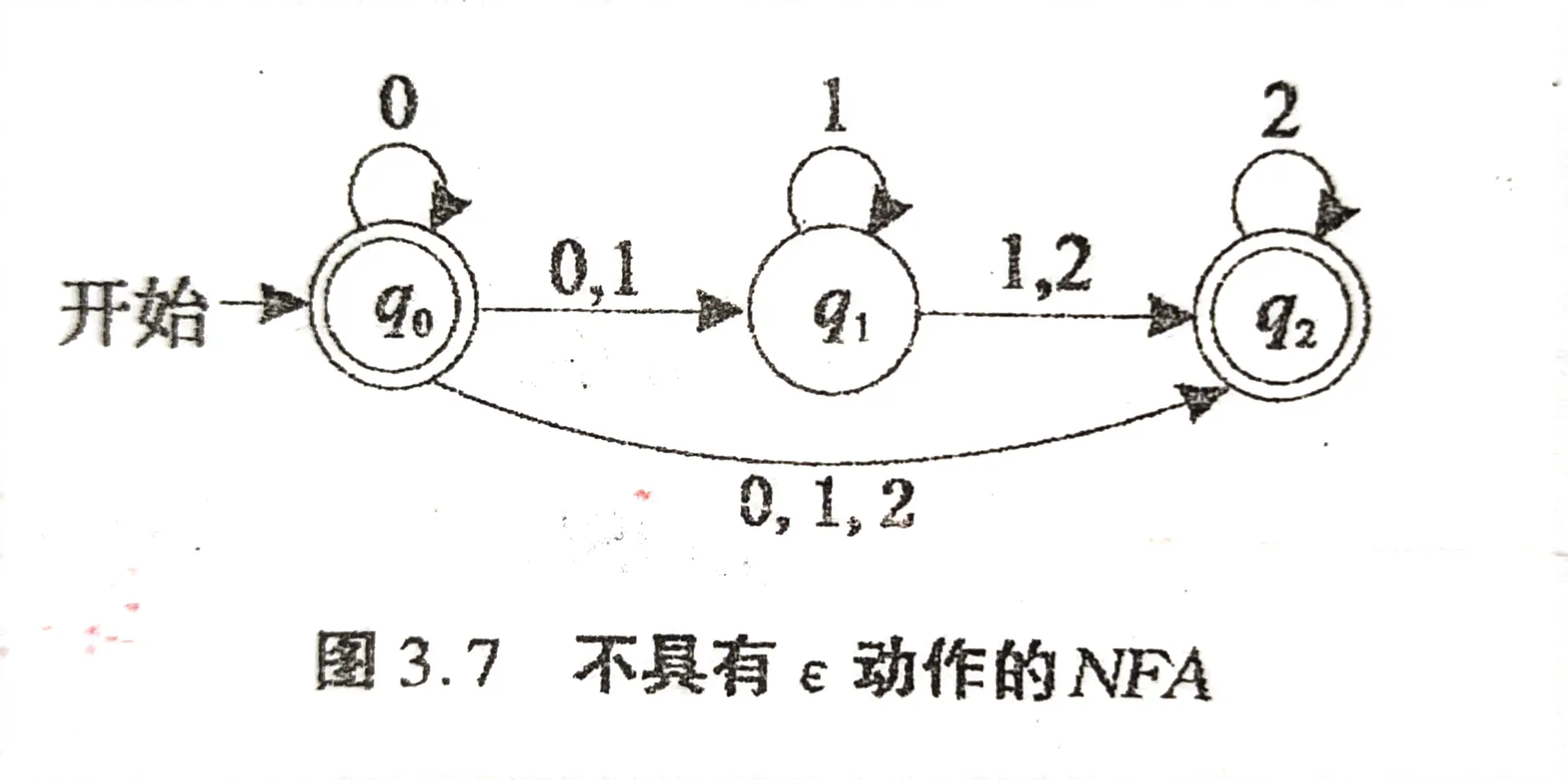 |
RL → ε \to\varepsilon →ε-NFA
算法描述
算法:将基础和正则表达式的三种运算用不同的 ε \varepsilon ε-NFA 处理:
| 基础 | 或 |
|---|---|
 | 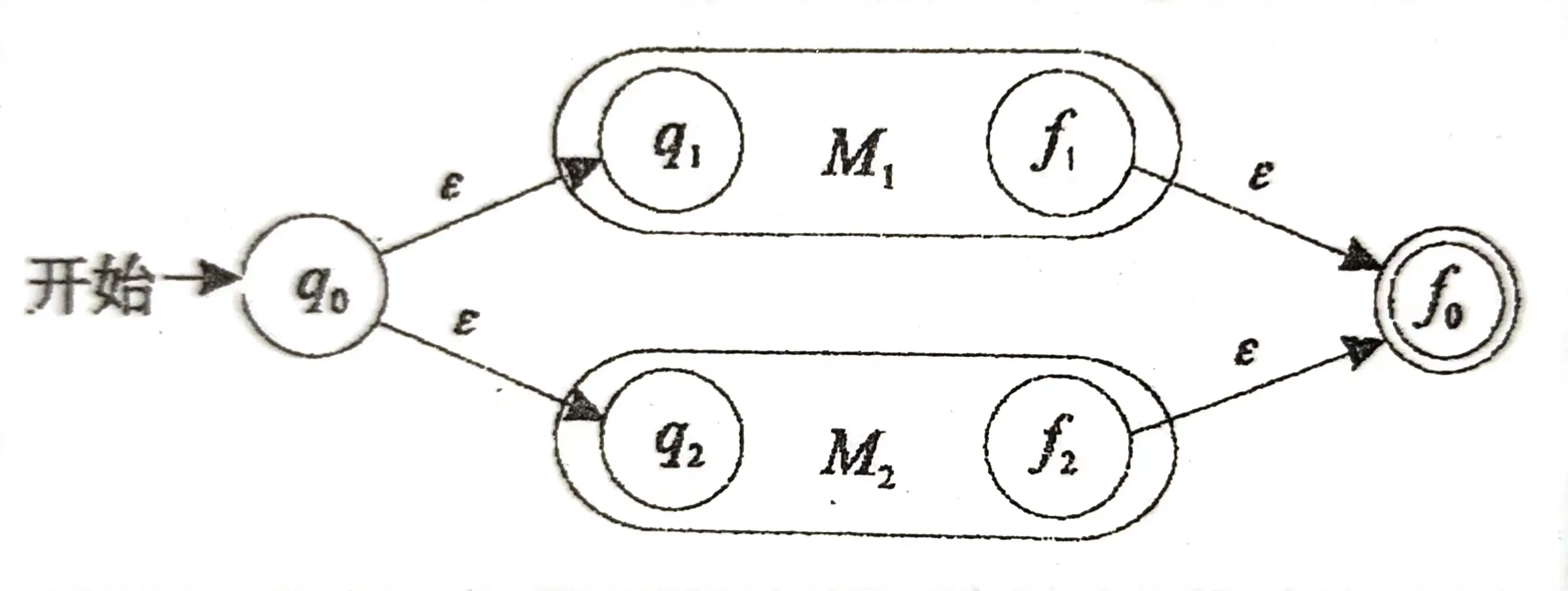 |
| 连接 | 闭包 |
 | 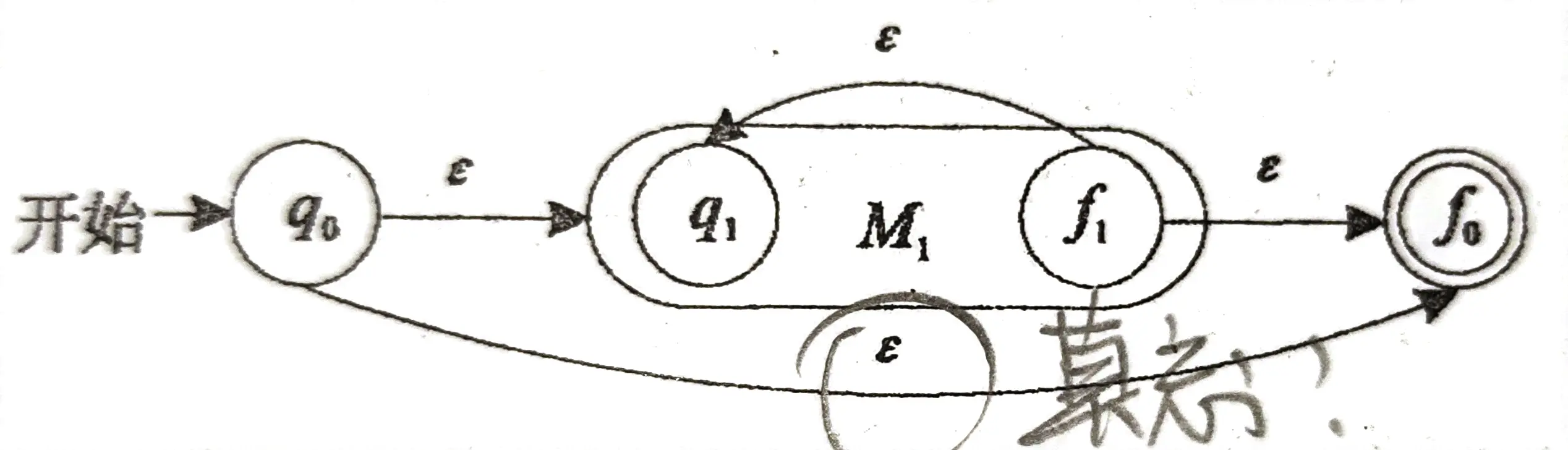 |
例题
例:将 10*+0 构造成一个 NFA

DFA → \to → RL
算法描述
算法:将 DFA 中所有状态标上序号,引入记号
R
i
j
k
R^k_{ij}
Rijk ,其含义是从序号为
i
i
i 到序号为
j
j
j 的状态的路径中所经过状态序号不大于
k
k
k (不包括
i
i
i 、
j
j
j 本身)的字符串集合,递推公式为:
R
i
j
0
=
{
{
a
∣
δ
(
q
i
,
a
=
q
j
)
}
,
i
f
i
≠
j
{
a
∣
δ
(
q
i
,
a
=
q
j
)
}
∪
{
ε
}
,
i
f
i
=
j
R^0_{ij}=\left \{ \begin{array}{ll} \{a|{\delta}(q_i,a=q_j)\},{\quad}{\quad}{\quad}if{\,}{\,}{\,}{\,}i{\not}=j\\ \{a|{\delta}(q_i,a=q_j)\}{\cup}\{ {\varepsilon}\},{\quad}if{\,}{\,}{\,}{\,}i=j \end{array} \right.\\
Rij0={{a∣δ(qi,a=qj)},ifi=j{a∣δ(qi,a=qj)}∪{ε},ifi=j
R i j k = R i k k − 1 ( R k k k − 1 ) ∗ R k j k − 1 ∪ R i j k − 1 R^k_{ij}=R^{k-1}_{ik}(R^{k-1}_{kk})^{\ast}R^{k-1}_{kj}{\,}{\cup}{\,}R^{k-1}_{ij} Rijk=Rikk−1(Rkkk−1)∗Rkjk−1∪Rijk−1
递推公式第二条第一部分的意思是,如果有经过状态序号为 k k k 的状态,则将这部分拆分开来
(具体用表格实现, k = 0 k=0 k=0 的情况直接根据 DFA 的转移路径写出;若有 n n n 个状态,则 k = n k=n k=n 的情况不要全部写出来,而是只写出 q j ∈ F q_j{\,}{\in}{\,}F qj∈F 的情况)
例题
例:给定如图 DFA,写出代表该自动机所接受的语言集合的正规表达式:
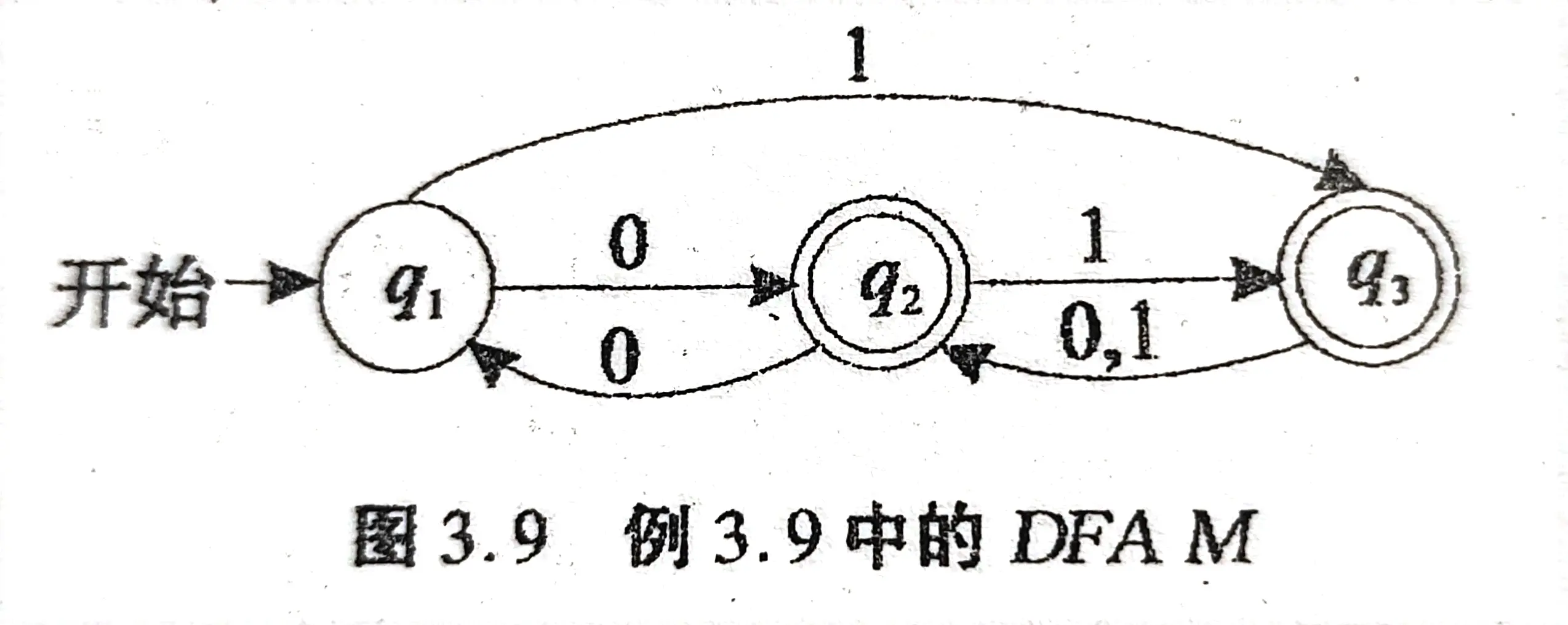
表格:
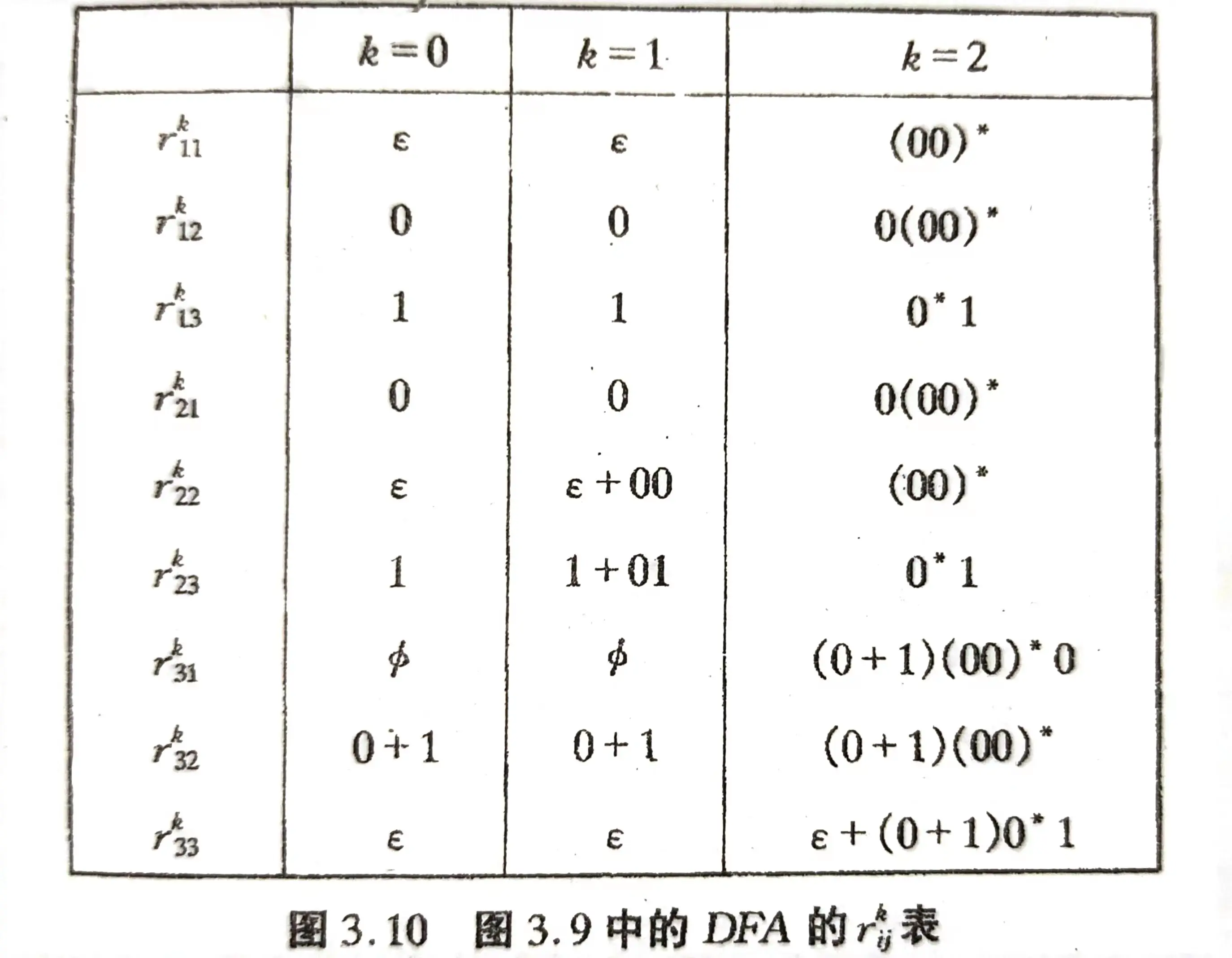
最后 q 2 q_2 q2 和 q 3 q_3 q3 是终结状态,因此只需求出:
-
r 12 3 = r 13 2 ( r 33 2 ) ∗ r 32 2 + r 12 2 = 0 ∗ 1 ( ( 0 + 1 ) 0 ∗ 1 ) ∗ ( 0 + 1 ) ( 00 ) ∗ + 0 ( 00 ) ∗ r^3_{12}=r^2_{13}(r^2_{33}){\ast}r^2_{32}+r^2_{12}=0^{\ast}1((0+1)0^{\ast}1)^{\ast}(0+1)(00)^{\ast}+0(00)^{\ast} r123=r132(r332)∗r322+r122=0∗1((0+1)0∗1)∗(0+1)(00)∗+0(00)∗
-
r 13 3 = r 13 2 ( r 33 2 ) ∗ r 33 2 + r 13 2 = 0 ∗ 1 ( ( 0 + 1 ) 0 ∗ 1 ) ∗ r^3_{13}=r^2_{13}(r^2_{33}){\ast}r^2_{33}+r^2_{13}=0^{\ast}1((0+1)0^{\ast}1)^{\ast} r133=r132(r332)∗r332+r132=0∗1((0+1)0∗1)∗
因此所求正则表达式为: r 12 3 + r 13 3 = 0 ∗ 1 ( ( 0 + 1 ) 0 ∗ 1 ) ∗ ( ( 0 + 1 ) ( 00 ) ∗ + ε ) + 0 ( 00 ) ∗ r^3_{12}+r^3_{13}=0^{\ast}1((0+1)0^{\ast}1)^{\ast}((0+1)(00)^{\ast}+{\varepsilon})+0(00)^{\ast} r123+r133=0∗1((0+1)0∗1)∗((0+1)(00)∗+ε)+0(00)∗
具有输出的有穷自动机
Moore机
Moore 机是六元组 M = ( Q , Σ , Δ , δ , λ , q 0 ) M=(Q,\Sigma,\Delta,\delta,\lambda,q_0) M=(Q,Σ,Δ,δ,λ,q0) ,其中:
- Δ \Delta Δ 是输出字母表
- λ \lambda λ 是输出函数, λ : Q → Δ \lambda:\,Q\to\Delta λ:Q→Δ
(无所谓接受或者拒绝,所以不需要终结状态;每个状态对应一个输出,因此输出序列比输入序列长度大一)
Mealy 机
Mealy 机是六元组 M = ( Q , Σ , Δ , δ , λ , q 0 ) M=(Q,\Sigma,\Delta,\delta,\lambda,q_0) M=(Q,Σ,Δ,δ,λ,q0) ,其中:
- Δ \Delta Δ 是输出字母表
- λ \lambda λ 是输出函数, λ : Q × Σ → Δ \lambda:\,Q\times\Sigma\to\Delta λ:Q×Σ→Δ
(每次转移对应一个输出,因此输出序列和输入序列长度相等)
Moore机 → \to → Mealy机
算法:将所有转状态结点的输出移动到其入边,作为其入边的输出;(相当于提前半个周期,在不考虑第一个输出字符的情况下二者等价)
Mealy机 → \to → Moore机
算法:无法向上边一样,直接将输出向后推半个周期作为入状态的输出,因为一个状态会作为多个入边的入状态;因此需要将状态进行拆分,每条不同的入边都需要对应一个新的状态
图示
| Moore to Mealy | Mealy to Moore |
|---|---|
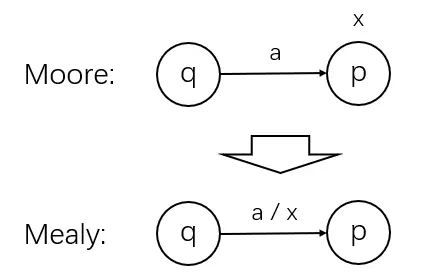 | 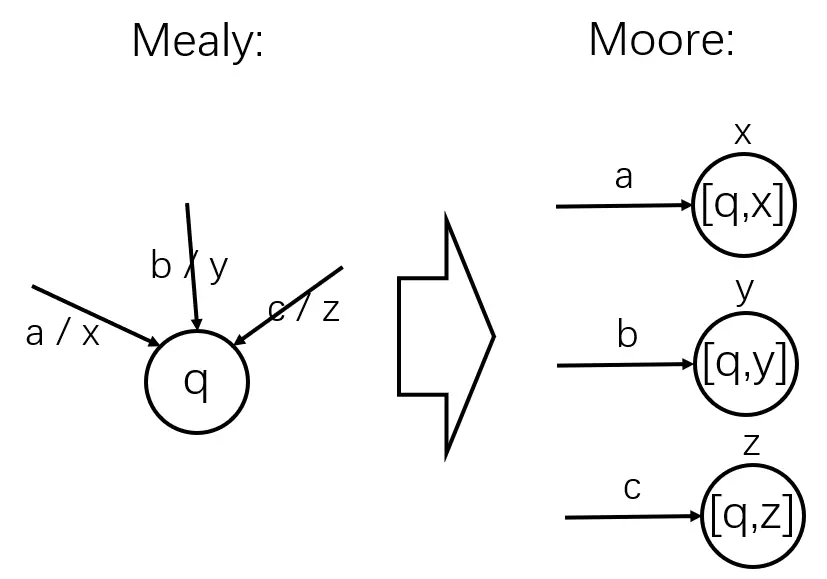 |























 2001
2001











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










