计算机图形学 第六章 图形变换

计算机图形学 第六章 图形变换

这章一般只考一道题（10分左右）

数学基础

（都是线性代数的知识，这里略写）

齐次坐标： 将一个原本是 $n$ 维的向量用一个 $n+1$ 维向量来表示

• 如 $(x_1,x_2,...x_n)$ 的其次坐标表示为 $(h{x}_1,h{x}_2,...,h{x}_n,h)$ ，其中 $h$ 是一个实数；

• 普通物理坐标与齐次坐标是一对多的关系

几何变换

要会写不同变换的矩阵

窗口区到视图区的坐标变换

需求： 实际的窗口区与视图区往往不一样大，需要从窗口区变换到视图区

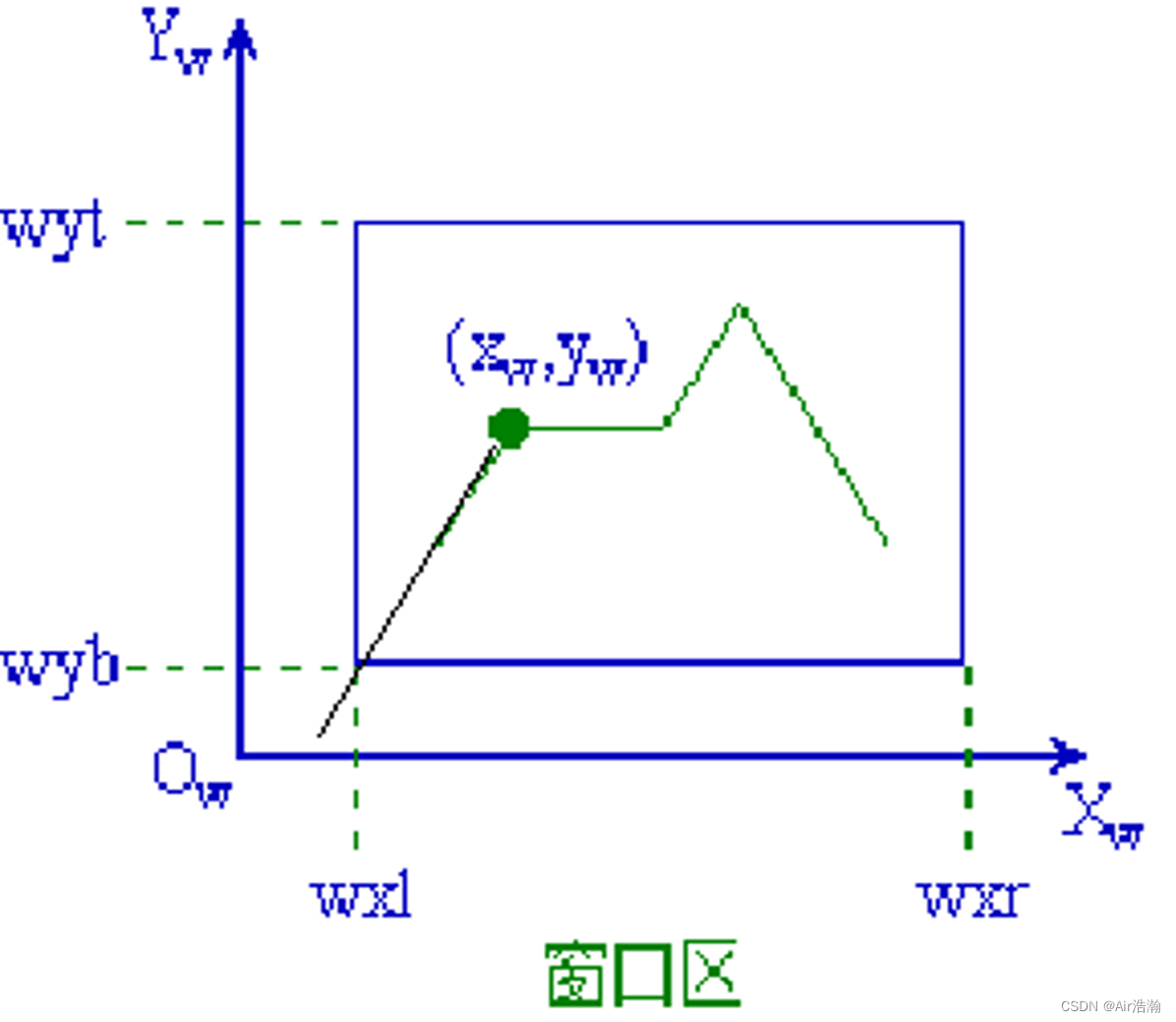变换公式： （就很简单的线性变化）（左式可以用右式表示，abcd 的值自己求一下）
$$\{\begin{array}{c}{x}_v-vxl=\frac{vxr-vxl}{wxr-wxl}(x_w-wxl)\\ y_v-vyl=\frac{vyr-vyl}{wyr-wyl}(y_w-wyl)\end{array}\{\begin{array}{c}{x}_v=a{x}_w+b\\ y_v=c{y}_w+d\end{array}$$

二维齐次坐标变换

矩阵都要会写，尤其注意错切的变换特点，会画示意图

二位齐次坐标： 矩阵形式如下，每一个部分都有特殊含义：

• $\left[\begin{array}{cc}a& b\\ d& e\end{array}\right]$ 可以对图形进行 缩放、旋转、对称、错切 等变换
• $\left[\begin{array}{c}c\\ f\end{array}\right]$ 是对图形进行 平移 变换
• $\left[\begin{array}{cc}g& h\end{array}\right]$ 是对图形作 投影 变换
• $[i]$ 是对图形整体进行 缩放 变换

基本变换

平移：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]=T(t_x,t_y)\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$

缩放：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}{s}_{x}x\\ s_{y}y\\ 1\end{array}\right]=S(s_x,s_y)\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$

旋转：绕原点旋转 $\theta$ 角：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x\cos \theta -y\sin \theta \\ x\sin \theta +y\cos \theta \\ 1\end{array}\right]=R(\theta )\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$

（旋转时逆时针 $\theta$ 为正）

对称：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}a& b& 0\\ d& e& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}x& y& 1\end{array}\right]=\left[\begin{array}{c}ax+by\\ dx+ey\\ 1\end{array}\right]$

• $b=d=0$ ，$a=-1$ ，$e=1$ 时，关于 $y$ 轴对称
• $b=d=0$ ，$a=1$ ，$e=-1$ 时，关于 $x$ 轴对称
• $b=d=0$ ，$a=e=-1$ 时，关于原点对称
• $b=d=1$ ，$a=e=0$ 时，关于 $y=x$ 对称
• $b=d=-1$ ，$a=e=0$ 时，关于 $y=-x$ 对称

错切：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& b& 0\\ d& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}x& y& 1\end{array}\right]=\left[\begin{array}{c}x+by\\ dx+y\\ 1\end{array}\right]$

• 当 $d=0$ 时，图形 $y$ 坐标不变，$x$ 坐标随初值和变换系数 $b$ 作线性变化（skewX）
• 当 $b=0$ 时，图形 $x$ 坐标不变，$y$ 坐标随初值和变换系数 $d$ 作线性变化（skewY）

复合变换

注意矩阵乘法的顺序

复合平移： 就是两次平移加起来
$$T(t_{x2},t_{y2})T(t_{x1},t_{y1})=\left[\begin{array}{ccc}1& 0& t_{x2}\\ 0& 1& t_{y2}\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& t_{x1}\\ 0& 1& t_{y1}\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_{x2}+t_{x1}\\ 0& 1& t_{y2}+t_{y1}\\ 0& 0& 1\end{array}\right]=T(t_{x2}+t_{x1},t_{y2}+t_{y1})$$
复合缩放：就是两次缩放相乘
$$S(s_{x2},s_{y2})S(s_{x1},s_{y1})=\left[\begin{array}{ccc}{s}_{x2}& 0& 0\\ 0& s_{y2}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{s}_{x1}& 0& 0\\ 0& s_{y1}& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}{s}_{x2}{s}_{x1}& 0& 0\\ 0& s_{y2}{s}_{y1}& 0\\ 0& 0& 1\end{array}\right]=S(s_{x2}{s}_{x1},s_{y2}{s}_{y1})$$
复合旋转： 就是两次的角度相加
$$R({\theta }_1)R({\theta }_2)=\left[\begin{array}{ccc}\cos {\theta }_1& -\sin {\theta }_1& 0\\ \sin {\theta }_1& \cos {\theta }_1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos {\theta }_2& -\sin {\theta }_2& 0\\ \sin {\theta }_2& \cos {\theta }_2& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}\cos ({\theta }_1+{\theta }_2)& -\sin ({\theta }_1+{\theta }_2)& 0\\ \sin ({\theta }_1+{\theta }_2)& \cos ({\theta }_1+{\theta }_2)& 0\\ 0& 0& 1\end{array}\right]=R({\theta }_1+{\theta }_2)$$
参考点变换： 以上缩放和旋转变换操作都是相对于原点的，如果要相对于任意参考点 $(x_f,y_f)$ ，则可以先平移到原点，再进行缩放、旋转变换，最后平移回去，即：（变换的顺序要从右到左看这个矩阵）
$$\begin{gathered} S(x_f,y_f;s_x,s_y)=T(x_f,y_f)S(s_x,s_y)T(-x_f,-y_f)=\left[\begin{array}{ccc}{s}_x& 0& x_f(1-s_x)\\ 0& s_y& y_f(1-s_y)\\ 0& 0& 1\end{array}\right] \\ R(x_f,y_f;\theta )=T(x_f,y_f)R(\theta )T(-x_f,-y_f)=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & x_f(1-\cos \theta )+y_f\sin \theta \\ \sin \theta & \cos \theta & y_f(1-\cos \theta )+x_{f}sin\theta \\ 0& 0& 1\end{array}\right] \end{gathered}$$

三维齐次坐标变换

经常考绕空间中任意轴旋转

三位齐次坐标： 矩阵形式如下，每一个部分都有特殊含义：

• $\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$ 可以对图形进行 缩放、旋转、错切 等变换
• $\left[\begin{array}{c}{a}_{14}\\ a_{24}\\ a_{34}\end{array}\right]$ 是对图形进行 平移 变换
• $\left[\begin{array}{ccc}{a}_{41}& a_{42}& a_{43}\end{array}\right]$ 是对图形作 投影 变换
• $[a_{44}]$ 是对图形整体进行 缩放 变换

平移：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ z+t_z\\ 1\end{array}\right]=T(t_x,t_y,t_z)\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

缩放： $\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}{s}_{x}x\\ s_{y}y\\ s_{z}z\\ 1\end{array}\right]=S(s_x,s_y,s_z)\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

参考点变换：参照 $(x_f,y_f,z_f)$ 缩放：
$$S(x_f,y_f,z_f;s_x,s_y,s_z)=T(x_f,y_f,z_f)S(s_x,s_y,s_z)T(-x_f,-y_f,-z_f)=\left[\begin{array}{cccc}{s}_x& 0& 0& x_f(1-s_x)\\ 0& s_y& 0& y_f(1-s_y)\\ 0& 0& s_z& z_f(1-s_z)\\ 0& 0& 0& 1\end{array}\right]$$
旋转：绕某一轴旋转 $\theta$ 角

• 绕 $x$ 轴旋转：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=R_x(\theta )\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

• 绕 $y$ 轴旋转：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=R_y(\theta )\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

• 绕 $z$ 轴旋转：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=R_x(\theta )\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

• 绕任意轴旋转：旋转轴 $AB$ 由 $A(x_a,y_a,z_a)$ 和方向 $(a,b,c)$ 定义：

  • 先将坐标原先移动到 $A$ 点，
  • 使 $AB$ 绕 $x$ 和 $y$ 轴分别旋转 $\alpha$ 角和 $\beta$ 角，使得 $AB$ 与 $z$ 轴重合（其中 $\alpha$ 和 $\beta$ 分别为 $AB$ 在 YOZ 平面和 XOZ 平面与 Z 轴的夹角）
  • 将 $P$ 绕 $z$ 轴旋转 $\theta$ 角
  • 做上述变换的逆变换

$$R_{AB}=T_A{R}_x{R}_y{R}_z{R}_y^{-1}{R}_x^{-1}{T}_A^{-1}$$

投影变换

画三视图考过简答题

投影变换的类别：

正平行投影：投影方向垂直于投影平面的平行投影，即三视图，按照如下顺序，主视图 $y=0$ ，侧视图 $x=0$ ，俯视图 $z=0$ ：

给出图片，算斜平面投影公式

斜平行投影：投影方向不垂直于投影平面的平行投影；下图中观察平面为 $z=0$ ，点 $(x,y)$ 为点 $(x,y,z)$ 再观察平面上的正平行投影坐标（即 $(x,y,z)\to(x,y)\bot z=0 $），点 $(x^{\prime },y^{\prime })$ 为斜投影坐标，$(x,y)$ 与 $(x^{\prime },y^{\prime })$ 的距离为 $L$ ：（这里最好想象成 $(x,y,z)$ 的 $z$ 是正的）

有 $x^{\prime }=x+L\cos \alpha$ ，$y^{\prime }=y+L\sin \alpha$ ；而 $z=L\tan \beta$ ，故 $x^{\prime }=x+\frac{z}{\tan \beta }\cos \alpha$ ，$y^{\prime }=y+\frac{z}{\tan \beta }\sin \alpha$ ；令 $l_1=\frac{1}{\tan \beta }$ ，则：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& l_1\cos \alpha & 0\\ 0& 1& l_1\sin \alpha & 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$
透视投影：视线（投影线）是从视点（观察点）出发，视线是不平行的。

• 灭点：不平行于投影平面的视线汇聚的一点称为灭点，在坐标轴上的灭点叫做主灭点。
• 类别：按照主灭点的个数分为：

按照以下图示，根据相似三角形的比例关系可以得到：

$$x^{\prime }=x(\frac{d_p}{z_{prp}-z})y^{\prime }=y(\frac{d_p}{z_{prp}-z})$$
用齐次坐标表示为：
$$\left[\begin{array}{c}{x}_h\\ y_h\\ z_h\\ h\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -z_{vp}/d_p& z_{vp}(z_{prp}/d_p)\\ 0& 0& -1/d_p& z_{prp}/d_p\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$
其中 $h=\frac{z_{prp}-z}{d_p}$ （这里 $x_h$ 等并不是投影过后的坐标；投影过后的坐标应该是 $x^{\prime }=\frac{x_h}{h}$ ）