文章目录
并行分布式计算 并行算法常用设计技术
这里讲了很多经典并行算法~
划分设计技术
均匀划分 - PSRS
n n n 个元素, p p p 台处理器,直接将 n n n 个元素分割为 p p p 端,每段含 n p \frac{n}{p} pn 个元素,并且分配给一台处理器。
MIMD 模型上的 Parallel Sorting by Regular Sampling
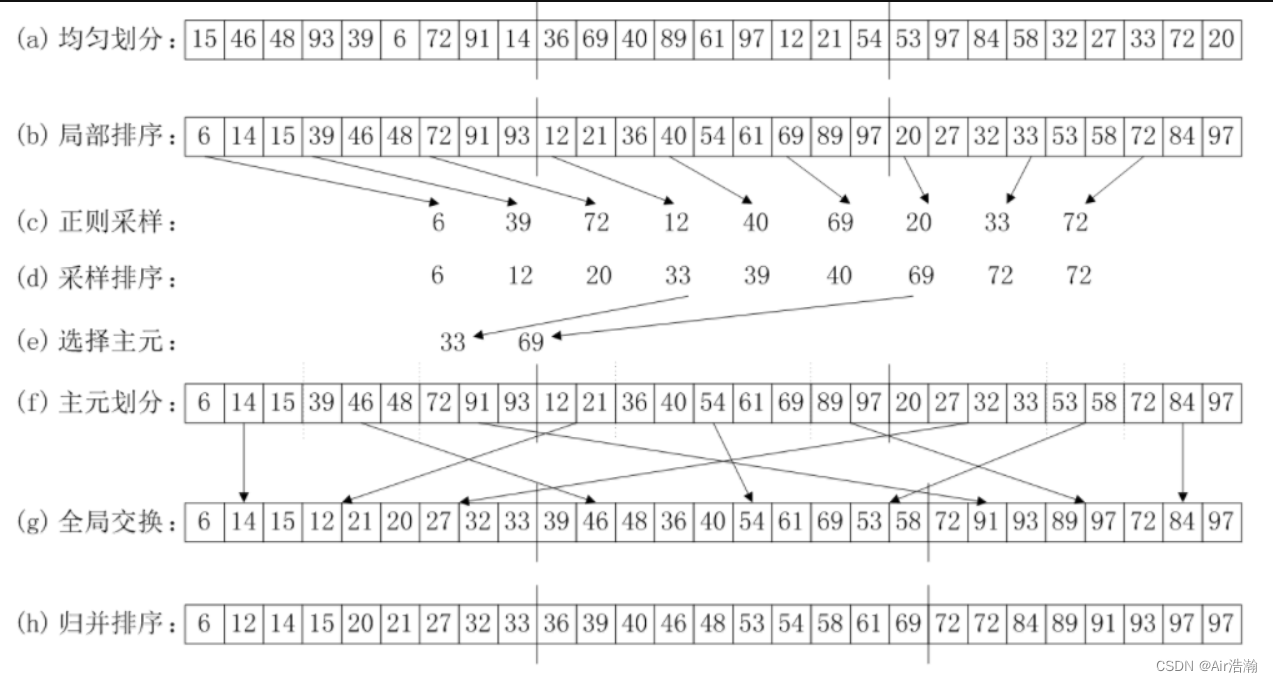
这里 n = 27 n=27 n=27 , p = 3 p=3 p=3 ;MIMD 的内存不共享:
① 均匀划分:将 n n n 个元素均匀划分为 p p p 段,按顺序分给每一个处理器;
② 局部排序:每个处理器调用串行排序算法进行排序;
③ 正则采样:每个处理器在自己的段上等间距地选取 p p p 个样本;
④ 样本排序:(比如由根进程)将采样 p 2 p^2 p2 个样本调用串行排序算法进行排序;
⑤ 选择主元:(比如由根进程)将排序后的样本均匀地选择 p − 1 p-1 p−1 个主元;
⑥ 主元划分:每个处理器根据自己段上数字和 p − 1 p-1 p−1 个主元的大小关系,划分为 p p p 个小段;
⑦ 全局交换:每个处理器将自己的第 i i i 小段发送给 i i i 号处理器;
⑧ 归并排序:每个处理器将自己留下的小段以及接收到的 p − 1 p-1 p−1 个小段进行归并排序
瓶颈在于 ⑦ 全局交换
方根划分- Valiant 归并算法
取每第 i n ( i = 1 , 2 , ⋯ ) i\sqrt{n}\,(i=1,\,2,\,\cdots) in(i=1,2,⋯) 个元素作为划分元素,将序列划分为若干段,再将序列划分为若干段,然后分段进行处理。
SIMD-CREW 上的 Valiant 归并算法

SIMD 共享内存、单个指令(类似GPU的环境),多个数据流需要执行同样的指令。
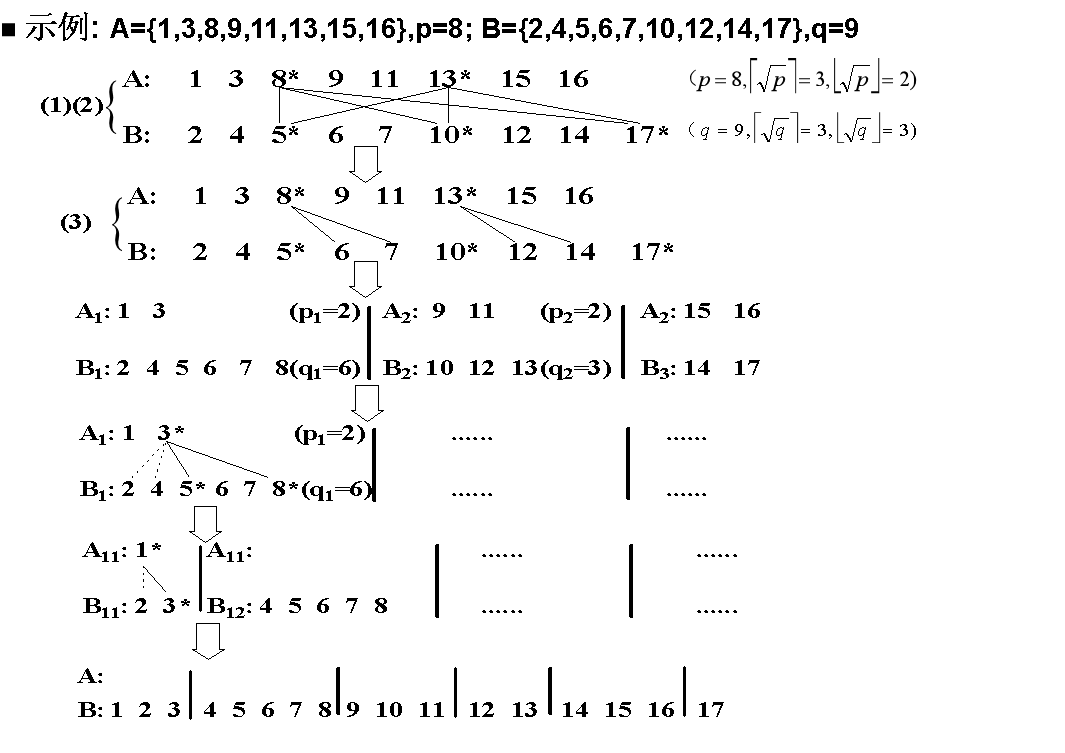
对数划分
取每第 i log n ( i = 1 , 2 , ⋯ ) i\log{n}\,(i=1,\,2,\,\cdots) ilogn(i=1,2,⋯) 个元素作为划分元素,将序列划分为若干段,再将序列划分为若干段,然后分段进行处理。

例如 X X X 中有两个数字(-13、7)比 13 小,因此 r a n k ( Y : X ) rank(Y:X) rank(Y:X) 的第一项是 2;
PRAM 多个进程、共享内存:

-
这个问题输出是,将 B B B 对数均匀划分,并且将 A A A 按照 B B B 的大小划分进行划分,最后输出 A A A 和 B B B 的每一段组合。(我感觉我解释得没有更好。。。)
-
算法中的 j ( i ) j(i) j(i) 数组代表 A i − 1 A_{i-1} Ai−1 的最后一个元素下标,也就是比 B i B_i Bi 小的、下标最大的 A A A 中的元素,这样 j ( i ) j(i) j(i) 和 j ( i + 1 ) j(i+1) j(i+1) 就可以确定 A i A_i Ai 的下标范围;(注意这里是 1-index 而不是 0-index)
-
这个问题可以作为排序问题的一个子问题,因为这样输出的 A i A_i Ai 和 B i B_i Bi 就可以进行归并排序,而且不影响整体的有序性。
功能划分
针对具体问题的情况进行划分,往往也是将 n n n 个元素划分成 p p p 组,每组中的元素个数应大于等于 m m m ,各组可并行处理。
(m,n)选择问题
问题:求出 n n n 个元素中前 m m m 个最小者;
输入: A = ( a 1 , … , a m ) A=(a_1,\,\dots,\,a_m) A=(a1,…,am)
输出:前 m m m 个最小者
算法:
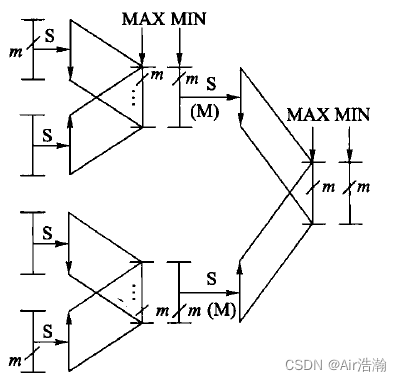
① 功能划分:将 A A A 划分为 g = n / m g=n/m g=n/m 组,每组含 m m m 个元素;
② 局部排序:使用 Batcher 排序网络将各组并行进行排序(两个有序序列总是可以组成一个双调序列);
③ 两两比较:将所排序的各组,两组两组地进行比较,从而形成 M I N MIN MIN 序列;
④ 排序-比较:对各个 M I N MIN MIN 序列。重复执行 ② 和 ③ ,直到选出 m m m 个最小者
分治设计技术
基本步骤:
- 将输入划分成若干规模相等的子问题;
- 并行地递归求解这些子问题;
- 并行地归并子问题的解,直到得到原问题的解。
关键在于如何分解子问题,最好子问题之间不需要通信。
双调归并网络
双调序列:一个序列 x 1 , x 2 , ⋯ , x n − 1 x_1,\,x_2,\,\cdots,\,x_{n-1} x1,x2,⋯,xn−1 是双调序列(Bitonic Sequence),如果:
- 存在一个 x k x_k xk( 0 ≤ k ≤ n − 1 0\leq k\leq n-1 0≤k≤n−1) 使得 x 0 ≥ ⋯ ≥ x k ≤ x k + 1 ⋯ ≤ x n − 1 x_0 \geq \cdots \geq x_k \leq x_{k+1}\cdots \leq x_{n-1} x0≥⋯≥xk≤xk+1⋯≤xn−1 成立;
或者:
- 此序列能够循环旋转使得第一个条件成立
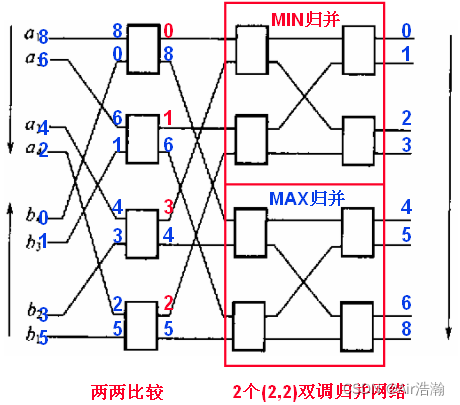
Batcher 定理:给定一个双调序列 x 1 , x 2 , ⋯ , x n − 1 x_1,\,x_2,\,\cdots,\,x_{n-1} x1,x2,⋯,xn−1 ,对于所有的 0 ≤ i ≤ n 2 − 1 0\leq i\leq \frac{n}{2}-1 0≤i≤2n−1 ,执行 x i x_i xi 和 x i + n 2 x_{i+\frac{n}{2}} xi+2n 的交换得到 s i = min { x i : x i + n 2 } s_i=\min\{x_i:x_{i+\frac{n}{2}}\} si=min{xi:xi+2n} 和 l i = max { x i : x i + n 2 } l_i=\max\{x_i:x_{i+\frac{n}{2}}\} li=max{xi:xi+2n} ,则:
- 所形成的小序列 M I N = ( s 0 , s 1 , ⋯ , s n 2 − 1 ) MIN=(s_0,\,s_1,\,\cdots,\,s_{\frac{n}{2}-1}) MIN=(s0,s1,⋯,s2n−1) 和大序列 M A X = ( l 0 , l 1 , ⋯ , l n 2 − 1 ) MAX=(l_0,\,l_1,\,\cdots,\,l_{\frac{n}{2}-1}) MAX=(l0,l1,⋯,l2n−1) 仍是双调序列;
- 对于所有的 0 ≤ i , j ≤ n 2 − 1 0\leq i,\,j\leq \frac{n}{2}-1 0≤i,j≤2n−1 ,满足 s i ≤ l i s_i\leq l_i si≤li ;
双调归并可以用比较器网络(Comparator Network)来实现,它是由 Batcher 比较器构成的。比较器是一个双输入和双输出的比较交换单元,可以将两输入中的较小者置于上输出端,而大者置于下输出端。
Batcher 双调归并算法
输入:双调序列 X = ( x 0 , x 1 , ⋯ , x n − 1 ) X=(x_0,\,x_1,\,\cdots,\,x_{n-1}) X=(x0,x1,⋯,xn−1) ;
输出:非降有序序列 Y = ( y 0 , y 1 , ⋯ , y n − 1 ) Y=(y_0,\,y_1,\,\cdots,\,y_{n-1}) Y=(y0,y1,⋯,yn−1) ;
算法:
def bitonic_merge(x):
for i in range(0, n/2) par-do:
s[i] = min{x[i], x[i+n/2]}
l[i] = max{x[i], x[i+n/2]}
MIN = bitonic_merge(s)
MAX = bitonic_merge(l)
return (MIN, MAX)
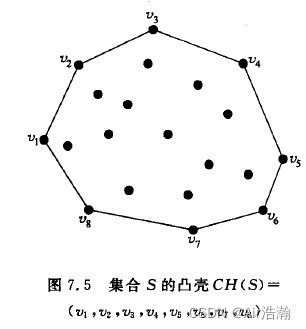
凸包问题
凸多边形:多边形 Q Q Q 上任意两点的连线均处于 Q Q Q 之内,则称多边形 Q Q Q 为凸多边形(Convex Polygon)
凸包:给定平面中 n n n 点集合 S = ( p 1 , p 2 , ⋯ , p n ) S=(p_1,\,p_2,\,\cdots,\,p_n) S=(p1,p2,⋯,pn) ,则 S S S 的凸包(Convex Hull)为包含 S S S 中所有点的最小凸多边形
求凸包的问题,就是要确定凸包边界上的有序定点列表 C H ( S ) CH(S) CH(S)
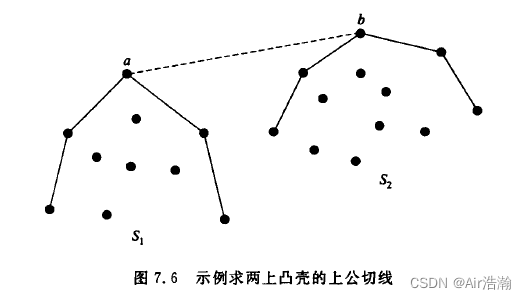
令 p p p 和 q q q 是 S S S 中 x x x 轴坐标最大和最小的两点,显然 p q pq pq 将凸包分为上凸包 U H ( S ) UH(S) UH(S) 和小土包 L H ( S ) LH(S) LH(S) ,且 C H ( S ) = U H ( S ) ∪ L H ( S ) CH(S)=UH(S)\cup LH(S) CH(S)=UH(S)∪LH(S) :
 |  |
|---|
输入: S = ( p 1 , p 2 , ⋯ , p n ) S=(p_1,\,p_2,\,\cdots,\,p_n) S=(p1,p2,⋯,pn) ,且已按照 x x x 轴坐标大小排序;
输出:上凸包顶点列表 U H ( S ) UH(S) UH(S)
算法:
def UpperHull(S):
if n <= 4:
暴力求出 UH(S) 并且 return
UH1 = UpperHull(S[1:n/2])
UH2 = UpperHull(S[n/2:n])
CT = CommonTangent(UH1, UH2)
通过 UH1, UH2 和 CT 构造 UH
return UH
平衡树设计技术
将输出元素作为叶节点构建一个平衡二叉树,中间节点为处理节点,自顶向下或自下而上进行并行处理。SIMD 非常适用于二叉树的模式。
求最大值
非常直接地两两比较,最终得到最大的那个:

前缀和
(也适用于求前缀积)串行算法需要 O ( n ) O(n) O(n) 的时间;
平衡树的并行算法如下:先自下而上地求和,在自顶向下将和播送到合适的位置。
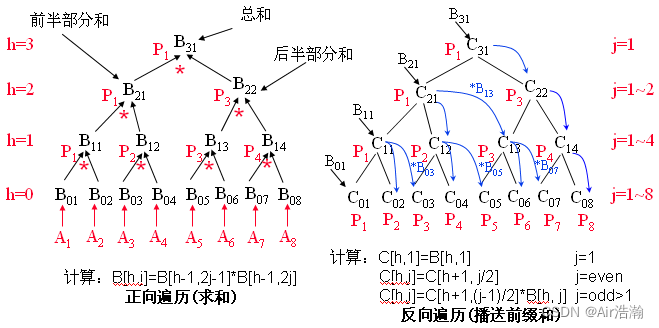

使用平衡树采用 SIMD-SM 的结构的前缀和算法,时间复杂度为 O ( 2 log n ) O(2\log n) O(2logn) ,需要 2 n − 1 2n-1 2n−1 个处理器。相比于 PRAM 结构,渐进复杂度相等,但是更不实用。
倍增设计技术
倍增设计(Doubling Technique),又称为指针跳跃(Pointer Jumping)技术,特别适合于处理链表或有向树之类的数据结构。
当递归调用时,所要处理数据之间的距离逐步加倍,经过 k k k 步以后即可完成距离为 2 k 2^k 2k 的所有数据的计算。
表序问题
问题: n n n 个元素的链表 L L L ,求出每个元素在 L L L 中的位序 rank,即距离表尾的距离

算法:next 数组代表结点的后继节点
par-do 初始化 next[k] 和 disance[k] # O(1)
执行 ceil(log(n)) 次: # O(logn)
对 k par-do: # O(1)
if next[k] != next[next[k]]: # 即 k 的后继不是 0 时
distance[k] = distance[k] + distance[next[k]]
next[k] = next[next[k]]
对 k par-do:
rank[k]=distance[k] # O(1)
时间复杂度 O ( n log n ) O(n\log n) O(nlogn) ,所需处理器为 p = n p=n p=n ;
流水线设计技术
就类似于体系结构里的流水线技术,每个进程执行流水线的一个阶段,通信模式也变得简单,只发生在相邻的阶段之间,可以完全地异步进行,可用于静态网络。可以有不止一条的流水线。
卷积


中间需要空一格是因为, x x x 和 y y y 的序列同时往中间移动。























 1283
1283











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










