Paper Reading【1】:Widar2.0: Passive Human Tracking with a Single Wi-Fi Link
“无线感知技术/非传感器场景感知技术”通过分析无线信号在传播过程中的变化,获得信号传播空间(信道)的特性,以实现场景的感知。这里的场景既包括人的因素(是否有人以及人的位置、姿势动作等),也包括其它外物的因素。非传感器感知将人类对物理世界的感知方式推动到了一个新的阶段——从以前单纯依赖部署专用传感器的方式升级为“专用”与“复用”相结合的方式。
无线感知技术将感知与通信合二为一,具有三个鲜明的特点:
“无传感器”:感知人和环境不再需要部署专门的传感器,这有别于无线传感网中有传感器负责感知而无线信号负责通信。“无线”:无须为通信及传感器部署有线线路。“无接触”:相较于现在市场上的各种可穿戴智能设备,无线传感更向前迈了一步,无须永和佩戴任何设备。
无线感知技术可以用于“被动式人员感知”。“被动式”指的是人员不需要携带任何电子设备,用以区别传统无线定位系统中,通过定位人所携带的电子设备来定位人员,这样的方式也被称作“设备非绑定的(device free)”或者“非侵入式的(non-invasive)”。
无线感知的局限性:
“有效特征湮没”:信号特征与背景环境相关,导致感知结果依赖部署环境,泛化能力差,学习训练成本高。(造成环境依赖性强的根本原因在于,已有研究工作提取的信号特征【 e . g e.g e.g. 信号幅度、相位等】严重依赖于系统部署的具体环境)。因此,不同的使用环境,不同的用户,甚至同一用户的不同位置、不同朝向等都会降低感知准确性,导致完全无法实现感知。针对新环境,需要重新采集数据进行训练,造成无线感知普适性差并且学习训练成本高。但令人遗憾的是,已有的工作绝大部分都是基于环境相关的信号特征来实现的。“识别模型简陋”:缺乏在无线信号空间对人的行为活动的精细时空建模,导致感知精度低、鲁棒性差。“数据集缺失”:高质量公开数据集的确实造成“性能比较”不客观、实验结果难复现、技术进步难积累。
既然无线信号在传播过程中“调制”了环境信息,那么如何从接收信号中“解调”这些环境信息呢?
e
.
g
e.g
e.g. 若手机接收到的
W
i
−
F
i
Wi-Fi
Wi−Fi信号较弱,可能是由于手机距离无线路由器较远;而若手机接收到的
W
i
−
F
i
Wi-Fi
Wi−Fi 信号强度骤降,很可能是由于手机进入了某些特定的封闭空间,如电梯。在该例中,可以用“接收信号强度(Received Signal Strength Indicator, RSSI)”为特征,推断手机的位置和所处的环境。信号特征的选取对于感知精度、可靠性、模型泛化能力等具有关键影响。
RSSI会因信号多径传播引起的小尺度阴影衰落而不再随传播距离增加单调递减,从而限制了测距精度。为刻画多径传播,无线信道通常可用“信道冲激响应(Channel Impulse Response, CIR)”或“频率响应(Channel Frequency Response, CFR)”来建模。现在,在普通的
W
i
−
F
i
Wi-Fi
Wi−Fi 设备上,可以以“信道状态信息(Channel State Information, CSI)”的形式获取一个采样版本的
C
F
R
CFR
CFR。
R
S
S
I
RSSI
RSSI只反映了多径叠加的总幅度,而
C
S
I
CSI
CSI 呈现了不同频率(对应不同子载波)下多径传播的幅度和相位,从而更加精确地刻画了具有频率选择性衰落信道特性的信道。
“相位信息”是
C
S
I
CSI
CSI 区别于
R
S
S
I
RSSI
RSSI 的一大特征。然而,受载波频率误差、采样频率偏差等因素的影响,
C
S
I
CSI
CSI 相位通常包含较多噪声。因此,
C
S
I
CSI
CSI 相位信息必须先处理再使用。
“波达角(Arrival of Angle, AoA)”与“飞行时间(TIme of Flight, ToF)”是雷达信号与声音定位、追踪目标时常用的两种特征。
“多普勒频偏(Doppler Frequency Shift, DFS)”也是一种常见的用于刻画人员活动与行为的特征,这是因为目标移动将导致经由目标反射的信号的路径长度产生变化,使得观测到的信号频率发生一定的偏移。对
C
S
I
CSI
CSI 功率进行时频分析(
e
.
g
e.g
e.g. 短时傅里叶变换和小波变换),可从功率的动态变化中提取人体运动导致的
D
F
S
DFS
DFS。一些工作进一步发现:只有目标的径向速度分量对应着反射路径长度的变化速率,提取到的
D
F
S
DFS
DFS 和运动速度方向、人员位置存在一定的几何约束关系。因此,通过添加更多链路可消除速度求解的歧义性,获得完整的人员速度信息,并用于定位、追踪、活动识别等多种场景。
前言
在本篇论文中,作者将 C S I CSI CSI 建模成关于幅度衰减、 D F S DFS DFS、 A o A AoA AoA 的函数,使用基于期望最大化的算法对多径信道的多参数进行联合估计,并利用图匹配技术得到经由目标反射路径的长度与目标的方位信息的最优解,最终实现了单链路下的分米级被动式人员追踪系统。
通过配置更多的发射天线,可对反射路径的
D
F
S
DFS
DFS、
T
o
F
ToF
ToF、
A
o
A
AoA
AoA 和“出发角(Angle of Departure, AoD)”进行联合估计,进一步提升单链路下的感知精度。
Abstract
本文介绍了"Widar2.0",这是第一个基于
W
i
−
F
i
Wi-Fi
Wi−Fi、可以在商品现货设备上使用单链路实现被动式人类跟踪和定位的系统。
1 INTRODUCTION
基于可见光和深度成像的技术已被提出商业化,但它们只跟踪定向视线附近的运动。相比之下,由于 W i − F i Wi-Fi Wi−Fi无处不在的部署和非视线部署的独特优势,基于 W i − F i Wi-Fi Wi−Fi 的方法变得更受欢迎。
一般情况下,被动 W i − F i Wi-Fi Wi−Fi 跟踪的工作原理是捕捉并分析人替反射的信号,从而刻下人体动作的特征。然而,建立一个无源跟踪系统是困难的,因为反射信号比直接接收的功率弱几个数量级,并且与接收器上其它物体的反射叠加在一起。
- 首先,建立了一个统一的模型,用于同时和联合估计多个参数,包括
A
o
A
AoA
AoA、
T
o
F
ToF
ToF、
D
F
S
DFS
DFS 和衰减。
A
o
A
AoA
AoA 从根本上受到天线数量的限制,
T
o
F
ToF
ToF 受到频率带宽的限制。虽然,推导任何一个参数都是很有挑战性的,但我们的目标是利用多个参数,这将提供多维正交和互补的信息,从而有机会避免位置跟踪需要多个链路。为此,作者设计了一个包含所有感兴趣参数的模型来量化用户运动和
C
S
I
CSI
CSI 之间的关系,将多参数估计问题表示为最大似然估计问题,并使用
"EM Algorithm"来有效求解得到准确的估计。 - 其次,通过对同一无线电(如接收机)上的天线的 C S I CSI CSI 使用共轭乘法消除随机相位噪声。所得到的共轭卷积不受相位噪声的影响,同时仍可用于多参数估计。
- 第三,提出了新的算法,从错误的参数估计得到精确的位置。参数算法输出多次反射的杂波参数。为了对目标定位,作者设计了一种基于图的算法来精确地识别目标在杂波多径参数反射下所对应的参数。原则上,跟踪可以简单地通过基于 A o A AoA AoA 和 T o F ToF ToF 得到的范围的几何推导来实现。
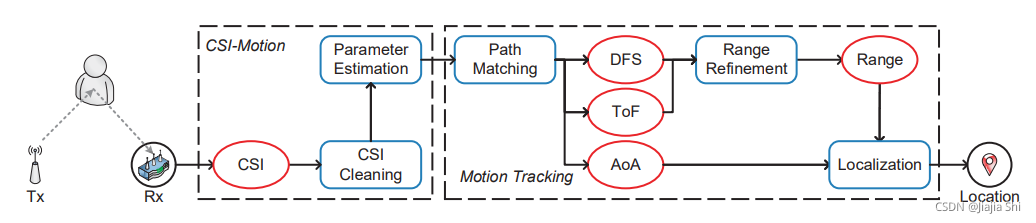
下图所示为"Widar2.0"的系统图:
2 OVERVIEW
"Widar2.0"的核心是通过在
C
O
T
s
COTs
COTs 设备上仅使用一个
W
i
−
F
i
Wi-Fi
Wi−Fi 链路实现亚米级的移动人员被动跟踪。关键是从单个链路寻找多个信号参数,而不是使用多个链路的单个参数,通过"CSI-motion Model"和"Motion Tracking Model"实现。
"CSI-motion Model"对来自噪声
C
S
I
CSI
CSI 的多径信号进行联合多参数估计。在接收到
C
S
I
CSI
CSI测量值后,"Widar2.0"首先对它们进行清洗。
C
S
I
CSI
CSI 清洗的目的有两个:
- 消除由异步收发机引起的随机 C S I CSI CSI 相位噪声;
- 超越静态路径( e . g e.g e.g. L o S LoS LoS 路径)的强信号,并放大运动目标发射的信号。
随后,"Widar2.0"应用参数估计算法获取多路径信号的多维参数 (
T
o
F
ToF
ToF、
A
o
A
AoA
AoA、
D
F
S
DFS
DFS、衰减)。
"Widar2.0"通过路径匹配模块从杂波估计中识别出运动目标所反映的信号所对应的感兴趣的参数,然后再距离细化模块中通过卡尔曼平滑器融合
T
o
F
ToF
ToF 和
D
F
S
DFS
DFS 来细化距离估计。最后,将估计的距离和
A
o
A
AoA
AoA 输入定位框架,得到运动目标的位置。
3 MOTION IN CSI
3.1 CSI-Motion Model
无线信道由于多径效应,在时间
t
t
t,频率
f
f
f 和传感器(天线)
s
s
s 处有以下测量:
H
(
t
,
f
,
s
)
=
∑
l
=
1
L
P
l
(
t
,
f
,
s
)
+
N
(
t
,
f
,
s
)
≜
∑
l
=
1
L
α
l
(
t
,
f
,
s
)
e
−
j
2
π
f
τ
l
(
t
,
f
,
s
)
+
N
(
t
,
f
,
s
)
\begin{align} H(t,f,s) &=\sum^L_{l=1}P_l(t,f,s)+N(t,f,s)\\ &\triangleq\sum^L_{l=1}\alpha_l(t,f,s)e^{-j2\pi f\tau_l(t,f,s)}+N(t,f,s) \end{align}
H(t,f,s)=l=1∑LPl(t,f,s)+N(t,f,s)≜l=1∑Lαl(t,f,s)e−j2πfτl(t,f,s)+N(t,f,s)
其中,
L
L
L 为多径总数;
P
l
P_l
Pl 为第
l
l
l 条多径;
α
l
\alpha_l
αl 为复衰减因子;
τ
l
\tau_l
τl 为传播时延;
N
N
N 为高斯白噪声。
W
i
−
F
i
Wi-Fi
Wi−Fi 网卡在时间(包)、频率(子载波)和空间(传感器)上分别测量信道。将第
i
i
i 个包、第
j
j
j 个载波、第
k
k
k 个传感器处的离散测量值记为
H
(
i
,
j
,
k
)
H(i,j,k)
H(i,j,k),以
H
(
0
,
0
,
0
)
H(0,0,0)
H(0,0,0) 为参考,则
H
(
i
,
j
,
k
)
H(i,j,k)
H(i,j,k) 中的第
l
l
l 条多径的信号相位(除以
2
π
2\pi
2π)变换为:
f
τ
l
(
i
,
j
,
k
)
=
(
f
c
+
△
f
j
)
(
τ
l
−
f
D
l
f
j
△
t
i
+
△
s
k
⋅
ϕ
l
)
≈
f
c
τ
l
+
△
f
j
τ
l
+
f
c
△
s
k
⋅
ϕ
l
−
f
D
l
△
t
i
f_{\tau_l} (i,j,k)=(f_c+\triangle f_j)(\tau_l-\frac{f_{D_l}}{f_j}\triangle t_i+\triangle s_k· \phi_l)\\ \approx f_c \tau_l+\triangle f_j \tau_l+f_c \triangle s_k ·\phi_l-f_{D_l}\triangle t_i
fτl(i,j,k)=(fc+△fj)(τl−fjfDl△ti+△sk⋅ϕl)≈fcτl+△fjτl+fc△sk⋅ϕl−fDl△ti
其中,
f
c
f_c
fc 为信道载波频率;
△
t
i
,
△
f
j
,
△
s
k
\triangle t_i,\triangle f_j,\triangle s_k
△ti,△fj,△sk 分别为
H
(
i
,
j
,
k
)
H(i,j,k)
H(i,j,k) 和
H
(
0
,
0
,
0
)
H(0,0,0)
H(0,0,0) 在时间,频率和空间位置上的差异;
τ
l
,
ϕ
l
,
f
D
l
\tau_l,\phi_l,f_{D_l}
τl,ϕl,fDl 分别是
H
(
0
,
0
,
0
)
H(0,0,0)
H(0,0,0) 中第
l
l
l 条多径的
T
o
F
ToF
ToF,(单位矢量方向)
A
o
A
AoA
AoA 和
D
F
S
DFS
DFS。
−
f
D
l
f
△
t
i
-\frac{f_{D_l}}{f} \triangle t_i
−ffDl△ti 反映了目标移动引起的
T
o
F
ToF
ToF 的变化,
△
s
k
⋅
ϕ
l
\triangle s_k· \phi_l
△sk⋅ϕl 为传感器之间的
T
o
F
ToF
ToF 差。省略二阶项,因为它们的数量级小于线性和常数项。
在短时间窗、窄带宽、小孔径的情况下,假定所有测量的信号衰减 α l \alpha_l αl 都是恒定的。此外, f c τ l f_c \tau_l fcτl 对所有测量值都是相同的,从参数估计的角度来看,可以合并到复衰减 α l \alpha_l αl 中。将第 l l l条路径的信号参数记为 θ l = ( α l , τ l , ϕ l , f D l ) \theta_l=(\alpha_l,\tau_l,\phi_l,f_{D_l}) θl=(αl,τl,ϕl,fDl),跟踪的第一步是估计目标所反映的信号的多维参数 θ \theta θ。
3.2 Joint Multiple Parameter Estimation
作者将参数估计问题转化为最大似然估计问题( M L E MLE MLE),并设计了包括 C S I CSI CSI 的参数估计算法。方便起见,令 m = ( i , j , k ) , i = 0 , 1 , . . . , T − 1 , j = 0 , 1 , . . . , F − 1 , k = 0 , 1 , . . . , S − 1 \bold{m}=(i,j,k),i=0,1,...,T-1,j=0,1,...,F-1,k=0,1,...,S-1 m=(i,j,k),i=0,1,...,T−1,j=0,1,...,F−1,k=0,1,...,S−1 为 C S I CSI CSI 测量 H ( i , j , k ) H(i,j,k) H(i,j,k) 的超域,其中 T , F , S T,F,S T,F,S 分别是包数、子载波数和传感器数。
给定测量观测值
h
(
m
)
h(\bold{m})
h(m),我们的目标是得到多维多径信号参数
Θ
\Theta
Θ 的最大似然估计(其中,
Θ
=
(
θ
l
)
l
=
1
L
\Theta=(\theta_l)^L_{l=1}
Θ=(θl)l=1L)。
Θ
\Theta
Θ 的对数似然函数是:
Λ
(
Θ
;
h
)
=
−
∑
m
∣
h
(
m
)
−
∑
l
=
1
L
P
l
(
m
;
θ
l
)
∣
2
\Lambda(\Theta;h)=-\sum_m |h(\bold{m})-\sum^L_{l=1}P_l(\bold{m};\theta_l)|^2
Λ(Θ;h)=−m∑∣h(m)−l=1∑LPl(m;θl)∣2
Θ
\Theta
Θ 的最大似然估计是最大化
Λ
\Lambda
Λ 的解:
Θ
^
M
L
=
a
r
g
m
a
x
{
Λ
(
Θ
;
h
)
}
\hat{\Theta}_{ML}=argmax \left\{\Lambda(\Theta;h)\right\}
Θ^ML=argmax{Λ(Θ;h)}
显然函数是非线性的且不存在闭合形式的解,而且随着
L
L
L 的增大直接搜索
Θ
^
M
L
\hat{\Theta}_{ML}
Θ^ML 的计算复杂度也升高。所以为了解决该问题,应用了“SAGE Algorithm(Space Alternating Generalized Expectation Maximization,空间交替广义最大化)”算法。
S
A
G
E
SAGE
SAGE 算法是
E
M
EM
EM 算法的拓展,该算法在每一次迭代仅仅重新估计
Θ
\Theta
Θ 的组件的一个子集而其它组件的估计不变。因此,我们可以将
Θ
\Theta
Θ 的估计分为多个单独参数的估计。
轮流对每条多径的参数最优化。具体来说,对于第
l
l
l 条多径,“期望步骤(e step)”是分解CSI并计算第
l
l
l 条多径的信号
P
l
P_l
Pl:
P
l
^
(
m
;
Θ
^
′
)
=
P
l
(
m
;
θ
l
′
^
)
+
β
l
(
h
(
m
)
−
∑
l
′
=
1
L
P
l
(
m
;
θ
l
′
′
^
)
)
\hat{P_l}(\bold{m};\hat{\Theta}')=P_l(\bold{m};\hat{\theta'_l})+\beta_l(h(\bold{m})-\sum_{l'=1}^LP_l(\bold{m};\hat{\theta'_{l'}}))
Pl^(m;Θ^′)=Pl(m;θl′^)+βl(h(m)−l′=1∑LPl(m;θl′′^))
其中,
Θ
^
′
\hat{\Theta}'
Θ^′ 是上一次迭代的参数估计值;
β
l
\beta_l
βl 是非负系数,用于控制算法的收敛速度,默认为
1
1
1。
Θ
\Theta
Θ 初始化为0。
整个算法流程为:

“最大化步骤(m step)”依次进行:
τ
^
l
′
′
=
a
r
g
m
a
x
τ
{
∣
z
(
τ
,
ϕ
^
l
′
,
f
^
D
l
′
;
P
^
l
(
m
;
Θ
^
′
)
)
∣
}
ϕ
^
l
′
′
=
a
r
g
m
a
x
ϕ
{
∣
z
(
τ
^
l
′
′
,
ϕ
,
f
^
D
l
′
;
P
^
l
(
m
;
Θ
^
′
)
)
∣
}
f
^
D
l
′
′
=
a
r
g
m
a
x
f
D
{
∣
z
(
τ
^
l
′
′
,
ϕ
^
l
′
′
,
f
D
;
P
^
l
(
m
;
Θ
^
′
)
)
∣
}
α
^
l
′
′
=
z
(
τ
^
l
′
′
,
ϕ
^
l
′
′
,
f
^
D
l
′
′
;
P
^
l
(
m
;
Θ
^
′
)
)
T
F
A
\hat{\tau}_l''=argmax_{\tau} \left\{|z(\tau,\hat{\phi}_l',\hat{f}_{D_l}';\hat{P}_l(\bold{m;\hat{\Theta}'}))|\right\} \\ \hat{\phi}_l''=argmax_{\phi} \left\{|z(\hat{\tau}_l'',\phi,\hat{f}_{D_l}';\hat{P}_l(\bold{m;\hat{\Theta}'}))|\right\}\\ \hat{f}_{D_l}''=argmax_{f_D} \left\{|z(\hat{\tau}_l'',\hat{\phi}_l'',f_D;\hat{P}_l(\bold{m};\hat{\Theta}'))|\right\}\\ \hat{\alpha}_l''=\frac{z(\hat{\tau}_l'',\hat{\phi}_l'',\hat{f}_{D_l}'';\hat{P}_l(\bold{m};\hat{\Theta}'))}{TFA}
τ^l′′=argmaxτ{∣z(τ,ϕ^l′,f^Dl′;P^l(m;Θ^′))∣}ϕ^l′′=argmaxϕ{∣z(τ^l′′,ϕ,f^Dl′;P^l(m;Θ^′))∣}f^Dl′′=argmaxfD{∣z(τ^l′′,ϕ^l′′,fD;P^l(m;Θ^′))∣}α^l′′=TFAz(τ^l′′,ϕ^l′′,f^Dl′′;P^l(m;Θ^′))
其中,
z
(
τ
,
ϕ
,
f
D
;
P
l
)
=
∑
m
e
2
π
Δ
f
j
τ
l
e
2
π
f
c
Δ
s
k
⋅
ϕ
l
e
−
2
π
f
D
l
Δ
t
i
P
l
(
m
)
z(\tau,\phi,f_D;P_l)=\sum_me^{2\pi \Delta f_j \tau_l}e^{2\pi f_c\Delta s_k \cdot \phi_l}e^{-2\pi f_{D_l}\Delta t_i}P_l(\bold{m})
z(τ,ϕ,fD;Pl)=m∑e2πΔfjτle2πfcΔsk⋅ϕle−2πfDlΔtiPl(m)
当"e step"的估计收敛时迭代结束,即连续估计之间的差值小于预定义的阈值。
3.3 CSI Cleaning
实际中,由于商业
W
i
−
F
i
Wi-Fi
Wi−Fi 的噪声较大,上述算法并不能直接适用于
C
S
I
CSI
CSI 测量。由于
C
S
I
CSI
CSI最初的目的是为了均衡信道进行数据解调,所以
C
S
I
CSI
CSI 不仅包含信道响应,还包含收发器之间的异步和硬件缺陷所造成的各种相位噪声。具体来说,
C
S
I
CSI
CSI 测量值
H
(
m
)
H(\bold{m})
H(m)的错误版本为:
H
~
(
m
)
=
H
(
m
)
e
2
π
(
Δ
f
j
ϵ
t
i
+
Δ
t
i
ϵ
f
)
+
ζ
s
k
\tilde{H}(\bold{m})=H(\bold{m})e^{2\pi(\Delta f_j \epsilon_{t_i}+\Delta_{t_i}\epsilon_f)+\zeta_{s_k}}
H~(m)=H(m)e2π(Δfjϵti+Δtiϵf)+ζsk
其中,
ϵ
t
i
\epsilon_{t_i}
ϵti和
ϵ
f
\epsilon_f
ϵf表示收发机之间的“定时偏移(TO)”和“载频偏移(CFO)”,
ζ
s
k
\zeta_{s_k}
ζsk 为接收传感器的初始相位。初始相位
ζ
s
k
\zeta_{s_k}
ζsk 在每次接收机启动时都是恒定的,因此可以手动校准。相比之下,
ϵ
t
i
\epsilon_{t_i}
ϵti 和
ϵ
f
\epsilon_f
ϵf 在数据包之间是不同的,需要对每个数据包进行估计。因此,从原始
C
S
I
s
CSIs
CSIs 中直接估计信号参数是不可能的。
为了滤除无关噪声,只保留感兴趣的信道响应,作者仔细分析带噪声的
C
S
I
CSI
CSI 的结构,提出了
C
S
I
CSI
CSI清洗算法。该算法的基础是,由
T
O
TO
TO 和
C
F
O
CFO
CFO 引起的相位噪声只在时间和频率上发生变化,而不在空间上发生变化。即同一“NIC(网络接口控制器【network interface controller】,又称网络接口控制器,网络适配器【network adapter】,网卡【network interface card】,或局域网接收器【LAN adapter】,是一块被设计用来允许计算机在计算机网络上进行通讯的计算机硬件)”的所有传感器同时经历相同的位置相位的噪声。因此,"Widar2.0"选择一个传感器作为参考传感器(
e
.
g
.
e.g.
e.g. 第
k
0
k_0
k0 个传感器),并计算每个传感器的
C
S
I
s
CSIs
CSIs 与参考传感器之间的共轭乘法
C
(
m
)
C(\bold{m})
C(m):
C
(
m
)
=
H
~
(
m
)
∗
H
~
∗
(
m
0
)
=
H
(
m
)
∗
H
∗
(
m
0
)
C(\bold{m})=\tilde{H}(\bold{m})*\tilde{H}^{*}(\bold{m}_0)=H(\bold{m})*H^*(\bold{m}_0)
C(m)=H~(m)∗H~∗(m0)=H(m)∗H∗(m0)
其中,
m
0
=
(
i
,
j
,
k
0
)
\bold{m}_0=(i,j,k_0)
m0=(i,j,k0)。
将多径信号分为静态组
P
s
P_s
Ps(
f
D
=
0
f_D=0
fD=0)和动态组
P
d
P_d
Pd(
f
D
≠
0
f_D \neq 0
fD=0),共轭乘法可分解为:
C
(
m
)
=
∑
n
1
,
n
2
∈
P
s
P
n
1
(
m
)
P
n
2
∗
(
m
0
)
+
∑
l
∈
P
d
,
n
∈
P
s
[
P
l
(
m
)
P
n
∗
(
m
0
)
+
P
n
(
m
)
P
l
∗
(
m
0
)
]
+
∑
l
1
,
l
2
∈
P
d
P
l
1
(
m
)
P
l
2
∗
(
m
0
)
C(\bold{m})=\sum_{n_1,n_2\in P_s}P_{n_1}(\bold{m})P_{n_2}^*(\bold{m}_0)\\+\sum_{l\in P_d,n\in P_s}[P_l(\bold{m})P_n^*(\bold{m}_0)+P_n(\bold{m})P_l^*(\bold{m}_0)]\\+\sum_{l_1,l_2\in P_d}P_{l_1}(\bold{m})P_{l_2}^*(\bold{m}_0)
C(m)=n1,n2∈Ps∑Pn1(m)Pn2∗(m0)+l∈Pd,n∈Ps∑[Pl(m)Pn∗(m0)+Pn(m)Pl∗(m0)]+l1,l2∈Pd∑Pl1(m)Pl2∗(m0)
上式中,由于静态信号不随时间变化,因此可以通过高通滤波器除去第一项求和。另一方面,由于静态信号比运动物体所反射的信号强得多,所以第三项求和项的阶数比前两项弱,可以忽略。
至于第二个求和项,对于任意的
l
∈
P
d
l\in P_d
l∈Pd和
n
∈
P
s
n\in P_s
n∈Ps,有:
P
l
(
m
)
P
n
∗
(
m
0
)
=
α
l
α
n
∗
e
−
2
π
Δ
f
j
(
τ
l
−
τ
n
)
−
2
π
f
c
Δ
s
k
⋅
ϕ
l
+
2
π
f
D
l
Δ
t
i
P
n
(
m
)
P
l
∗
(
m
0
)
=
α
n
α
l
∗
e
−
2
π
Δ
f
j
(
τ
n
−
τ
l
)
−
2
π
f
c
Δ
s
k
⋅
ϕ
n
−
2
π
f
D
l
Δ
t
i
P_l(\bold{m})P_n^*(\bold{m}_0)=\alpha_l\alpha_n^*e^{-2\pi \Delta f_j(\tau_l-\tau_n)-2\pi f_c \Delta s_k\cdot \phi_l+2\pi f_{D_l}\Delta_{t_i}}\\P_n(\bold{m})P_l^*(\bold{m}_0)=\alpha_n\alpha_l^*e^{-2\pi \Delta f_j(\tau_n-\tau_l)-2\pi f_c \Delta s_k\cdot \phi_n-2\pi f_{D_l}\Delta_{t_i}}
Pl(m)Pn∗(m0)=αlαn∗e−2πΔfj(τl−τn)−2πfcΔsk⋅ϕl+2πfDlΔtiPn(m)Pl∗(m0)=αnαl∗e−2πΔfj(τn−τl)−2πfcΔsk⋅ϕn−2πfDlΔti
***note:作者省略了
P
l
(
k
)
P
n
(
k
0
)
∗
P_l^{(k)}P_n^{(k_0)*}
Pl(k)Pn(k0)∗中的
e
−
2
π
f
c
Δ
s
k
0
⋅
ϕ
n
e^{-2\pi f_c\Delta s_{k_0}\cdot\phi_n}
e−2πfcΔsk0⋅ϕn 项和
P
n
(
k
)
P
l
(
k
0
)
∗
P_n^{(k)}P_l^{(k_0)*}
Pn(k)Pl(k0)∗ 中的
e
−
2
π
f
c
Δ
s
k
0
⋅
ϕ
l
e^{-2\pi f_c\Delta s_{k_0}\cdot\phi_l}
e−2πfcΔsk0⋅ϕl 项,因为这两项对所有的测量都是相同的且不会影响参数估计。
然而,共轭乘法产生的多余项
P
n
(
m
)
P
l
∗
(
m
0
)
P_n(\bold{m})P_l^*(\bold{m}_0)
Pn(m)Pl∗(m0) 将
T
o
F
ToF
ToF、
A
o
A
AoA
AoA和
D
F
S
DFS
DFS依次伪造成
(
τ
n
−
τ
l
)
(\tau_n-\tau_l)
(τn−τl),
ϕ
n
\phi_n
ϕn 和
−
f
D
l
-f_{D_l}
−fDl。为了粗略地消除该多余项,作者在所有传感器的CSI振幅中减去一个常数
β
\beta
β,并在参考传感器的
C
S
I
CSI
CSI 振幅中加上一个常数
γ
\gamma
γ。当
m
≠
m
0
\bold{m}\neq \bold{m}_0
m=m0时,有:
∣
P
n
(
m
)
P
l
∗
(
m
0
)
∣
=
(
∣
α
n
∣
−
β
)
∣
α
l
∣
<
<
∣
α
l
∣
(
∣
α
n
∣
+
γ
)
=
∣
P
l
(
m
)
P
n
∗
(
m
0
)
∣
|P_n(\bold{m})P_l^*(\bold{m}_0)|=(|\alpha_n|-\beta)|\alpha_l|<<|\alpha_l|(|\alpha_n|+\gamma)=|P_l(\bold{m})P_n^*(\bold{m}_0)|
∣Pn(m)Pl∗(m0)∣=(∣αn∣−β)∣αl∣<<∣αl∣(∣αn∣+γ)=∣Pl(m)Pn∗(m0)∣
因此,产生的多余项可以省略。作为对比, f i g u r e 3 b figure3 b figure3b 显示了作者基于共轭乘法的方法校准的 C S I s CSIs CSIs 的光谱图:
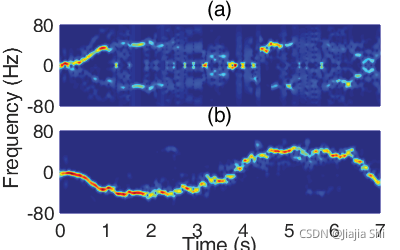
具体来说,"Widar2.0"将“CSI收集(CSI collection)”划分为“0.1 s段(0.1 s segments)”,其中信号参数假定为静态的,然后将参数估计算法应用到每一段,得到信号参数估计实例。
4 LOCALIZATION
虽然参数估计算法从清理后的 C S I CSI CSI 中产生多维信号参数,但由于多路径效应和低分辨率,这些估计通常是错误的。为了精确跟踪,需要更精确的参数。因此,在本节中,作者建议从杂波估计( S e c t i o n 4.1 Section 4.1 Section4.1)中识别感兴趣的反射路径相对应的参数,并通过利用正交维数中的参数( S e c t i o n 4.2 Section 4.2 Section4.2)来提高分辨率。之后,作者提出了一个基于 T o F ToF ToF 和单链路距离估计的目标定位框架( S e c t i o n 4.3 Section4.3 Section4.3)。
4.1 Path Matching
参数估计算法的输出由多径信号的参数组成。需要一个筛选程序来确定感兴趣的参数。然而,目标的反射参数的选择并不简单,因为所有的多径参数都是混杂在一起的。例如,下图显示了跟踪的典型多径信号参数,其中目标先远离链路然后回到链路。
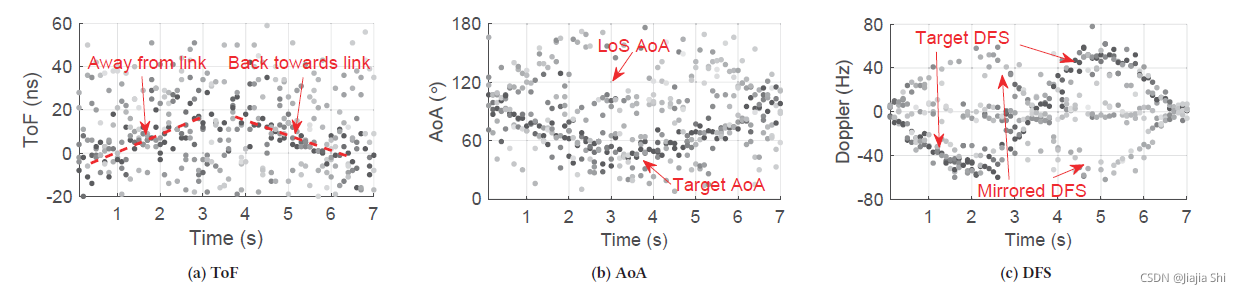
为了更好地说明,我们根据相应路径的衰减来加权参数的颜色。目标参数在散点图中很难被识别出来,容易与其它路径的参数和噪声混淆。例如, f i g u r e 5 b figure5 b figure5b 和 f i g u r e 5 c figure5 c figure5c 显示了多余项对应的参数。此外,由于我们滤除了大多数静态信号,剩下的部分可能包含更重要的噪声,通过分布的异常值表示。
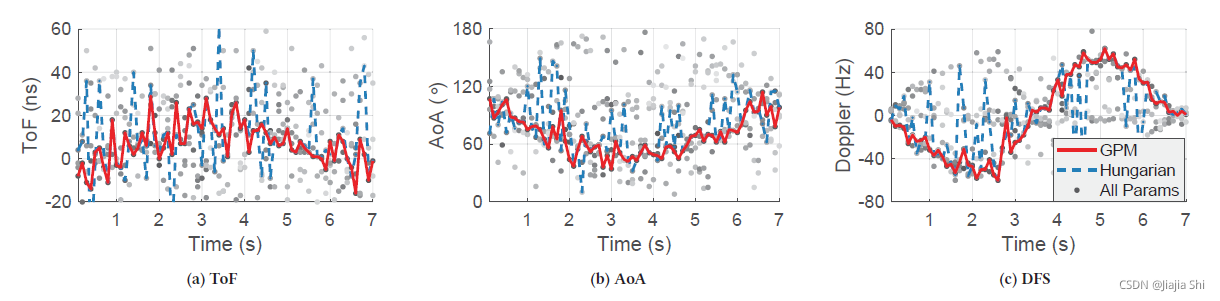
为了克服多径参数杂波中的噪声,作者提出了一种基于图的路径匹配算法,该算法可以同时匹配连续的多段。形式上,如 f i g u r e 6 figure6 figure6 所示:
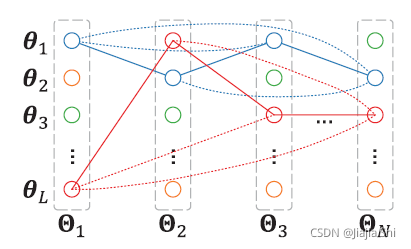
假设考虑
N
N
N 个
C
S
I
CSI
CSI 段的估计,每个估计都包含
L
L
L 条路径的参数,我们构建一个加权的“N部图(N-partite graph)”
G
=
(
V
,
E
,
W
)
G=(V,E,W)
G=(V,E,W),其中
v
i
j
∈
V
v_{ij}\in V
vij∈V 表示第
i
i
i 个估计
θ
i
j
\theta_{ij}
θij 中的第
j
j
j 条路径的参数;
e
i
1
j
1
i
2
j
2
∈
E
e_{i_1j_1}^{i_2j_2}\in E
ei1j1i2j2∈E 表示
v
i
1
j
1
v_{i_1j_1}
vi1j1与
v
i
2
j
2
v_{i_2j_2}
vi2j2 之间的边;
w
i
1
j
1
i
2
j
2
∈
W
w_{i_1j_1}^{i_2j_2}\in W
wi1j1i2j2∈W 表示边
e
i
1
j
1
i
2
j
2
e_{i_1j_1}^{i_2j_2}
ei1j1i2j2 的权值。权重定义为参数之间的距离:
w
i
1
j
1
i
2
j
2
=
w
i
2
j
2
i
1
j
1
=
∣
∣
c
T
(
θ
i
1
j
1
−
θ
i
2
j
2
)
∣
∣
w_{i_1j_1}^{i_2j_2}=w_{i_2j_2}^{i_1j_1}=||c^T(\theta_{i_1j_1-\theta_{i_2j_2}})||
wi1j1i2j2=wi2j2i1j1=∣∣cT(θi1j1−θi2j2)∣∣
其中,
c
c
c 为系数向量,对不同参数
T
O
F
TOF
TOF、
A
o
A
AoA
AoA、
D
F
S
DFS
DFS 和衰减进行归一化。
我们将
x
i
1
j
1
i
2
j
2
x_{i_1j_1}^{i_2j_2}
xi1j1i2j2 表示为二进制变量,表示是否选择边
e
i
1
j
1
i
2
j
2
e_{i_1j_1}^{i_2j_2}
ei1j1i2j2 进行匹配。因此,目标函数为:
x
o
p
t
=
a
r
g
m
i
n
x
w
T
x
x_{opt}=argmin_xw^{T}x
xopt=argminxwTx
其中,
w
w
w和
x
x
x分别是向量化的权重和变量。
为了确保所选边构成 N N N 阶完全图,需要满足几个约束条件:
- 不能选择第
i
−
t
h
i-th
i−th 部分(
p
a
r
t
part
part)的边:
x i j 1 i j 2 = 0 x_{ij_1}^{ij_2}=0 xij1ij2=0 - 在第
i
i
i 部分中选择的边数必须等于其余部分的顶点数:
∑ j 1 = 1 L ∑ i 2 = 1 , i 2 ≠ i 1 N ∑ j 2 = 1 L = L ( N − 1 ) \sum_{j_1=1}^L\sum_{i_2=1,i_2\neq i_1}^{N}\sum_{j_2=1}^L=L(N-1) j1=1∑Li2=1,i2=i1∑Nj2=1∑L=L(N−1) - 任意顶点
v
i
1
j
1
v_{i_1j_1}
vi1j1 与第
i
2
i_2
i2 部分中任意顶点之间的选定边数不得大于
1
1
1:
∑ j 2 = 1 L x i 1 j 1 i 2 j 2 ≤ 1 \sum_{j_2=1}^Lx_{i_1j_1}^{i_2j_2}\leq1 j2=1∑Lxi1j1i2j2≤1 - 若
e
i
1
j
1
i
2
j
2
e_{i_1j_1}^{i_2j_2}
ei1j1i2j2 和
e
i
2
j
2
i
3
j
3
e_{i_2j_2}^{i_3j_3}
ei2j2i3j3 被选定,则
e
i
1
j
1
i
3
j
3
e^{i_3j_3}_{i_1j_1}
ei1j1i3j3 一定会被选定:
x i 1 j 1 i 2 j 2 + x i 2 j 2 i 3 j 3 ≤ 1 + x i 1 j 1 i 3 j 3 x_{i_1j_1}^{i_2j_2}+x_{i_2j_2}^{i_3j_3}\leq1+x_{i_1j_1}^{i_3j_3} xi1j1i2j2+xi2j2i3j3≤1+xi1j1i3j3
这个约束是为了确保选择的边构成完整的图。
4.2 Range Refinement
理论上,反射路径与 L o S LoS LoS 路径的相对距离可以通过估算的 T o F ToF ToF 与光速相乘得到。然而,估计距离可能受到强噪声和低分辨率的 T o F ToF ToF 的影响。具体来说,作者采用的 T o F ToF ToF 估计分辨率为 1 n s 1 ns 1ns,对应于 0.3 0.3 0.3 米的范围。因此,几个 n s ns ns 的 T o F ToF ToF 误差可能导致数米的测距误差。 f i g u r e 7 figure7 figure7 显示了直接从 T o F ToF ToF 计算的范围。但是,距离的估计是波动的,因此不能用于定位。
为了优化距离估计,作者结合了绝对的粗粒度
T
o
F
ToF
ToF 和细粒度的相对
D
F
S
DFS
DFS,并提出了一种有效的平滑算法。具体来说,
D
F
S
DFS
DFS 相当于路径范围
v
v
v 的变化率:
f
D
=
v
λ
f_D=\frac{v}{\lambda}
fD=λv
其中
λ
\lambda
λ 为信号的波长,对于
5.8
5.8
5.8
G
H
z
GHz
GHz 的
W
i
−
F
i
Wi-Fi
Wi−Fi 信号,
λ
\lambda
λ 约为
0.05
m
0.05m
0.05m。因此,
D
F
S
DFS
DFS 估计的
1
H
z
1 Hz
1Hz 分辨率对应的路径距离变化率只有
0.05
m
/
s
0.05 m/s
0.05m/s。基于此观测,作者采用"Kalman Smoother (KS)"算法,利用
D
F
S
DFS
DFS 估计的路径距离变化率来细化
T
o
F
ToF
ToF 估计的范围。将过程噪声和观测噪声分别初始化为前
2
2
2 秒数据的方差。
f
i
g
u
r
e
7
figure7
figure7 显示了"Kalman Smoother"改善的范围,它比原始估计更平滑。根据相对距离,再加上发射机和接收机之间的恒定距离,就可以进一步推导出反射路径的绝对距离。
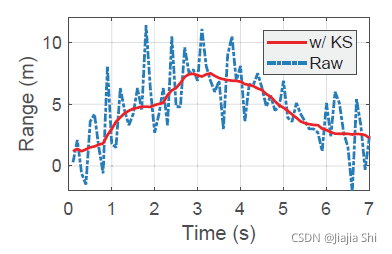
4.3 Localization Model
最后,"Widar2.0"使用导出的距离和
A
o
A
AoA
AoA 定位目标。
f
i
g
u
r
e
8
figure8
figure8 显示了定位框架。为了不失一般性,我们将发射机、接收机和目标的位置分别表示为
o
=
(
0
,
0
)
,
l
r
=
(
x
r
,
y
r
)
o=(0,0), l_r=(x_r, y_r)
o=(0,0),lr=(xr,yr) 和
l
=
(
x
,
y
)
l=(x, y)
l=(x,y)。
L
o
S
LoS
LoS 信号的
A
o
A
AoA
AoA,
ϕ
T
x
\phi _{T_x}
ϕTx 可以用
C
S
I
−
s
a
g
e
CSI- sage
CSI−sage 算法从原始
C
S
I
CSI
CSI 测量值中计算出来。此外,通过
ϕ
T
x
\phi _{T_x}
ϕTx和
(
x
r
,
y
r
)
(x_r,y_r)
(xr,yr) 可以计算出接收机阵列
ψ
r
\psi_r
ψr 的方位。反射路径的距离为
d
T
a
r
d_{T_{ar}}
dTar,反射路径的
A
o
A
AoA
AoA 为
ϕ
T
a
r
\phi_{T_{ar}}
ϕTar。
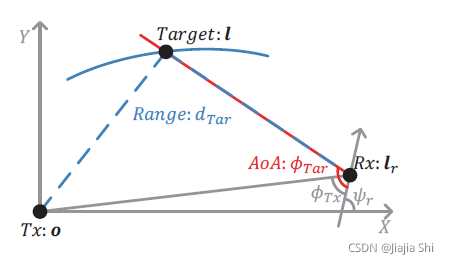
有以下方程组:
x
2
+
y
2
+
(
x
−
x
r
)
2
+
(
y
−
y
r
)
2
=
d
T
a
r
(
y
−
y
r
)
c
o
s
(
ψ
r
−
ϕ
T
a
r
)
=
(
x
−
x
r
)
s
i
n
(
ψ
r
−
ϕ
T
a
r
)
\sqrt{x^2+y^2}+\sqrt{(x-x_r)^2+(y-y_r)^2}=d_{T_{ar}}\\ (y-y_r)cos(\psi_r-\phi_{T_{ar}})=(x-x_r)sin(\psi_r-\phi_{T_{ar}})
x2+y2+(x−xr)2+(y−yr)2=dTar(y−yr)cos(ψr−ϕTar)=(x−xr)sin(ψr−ϕTar)
假设“跟踪区域(tracking area)”在链路的一侧,由距离确定的半椭圆与由
A
o
A
AoA
AoA 确定的半直线的交点的方程组可推导出唯一解。设接收端位于跟踪区域的
X
X
X 边界上,则上式方程组的闭合解为:
x
=
1
2
d
T
a
r
2
+
2
s
r
d
T
a
r
x
r
s
e
c
φ
+
x
r
2
s
e
c
2
φ
−
(
x
r
t
a
n
φ
y
r
)
2
x
r
+
y
r
t
a
n
φ
+
s
r
d
T
a
r
s
e
c
φ
y
=
t
a
n
φ
(
x
−
x
r
)
+
y
r
x=\frac{1}{2}\frac{d_{T_{ar}}^2+2s_rd_{T_{ar}}x_rsec\varphi+x_r^2sec^2\varphi-(x_rtan\varphi y_r)^2}{x_r+y_rtan\varphi + s_rd_{T_{ar}}sec\varphi}\\ y=tan \varphi(x-x_r)+y_r
x=21xr+yrtanφ+srdTarsecφdTar2+2srdTarxrsecφ+xr2sec2φ−(xrtanφyr)2y=tanφ(x−xr)+yr
其中,
φ
=
ψ
r
−
ϕ
T
a
r
,
s
r
=
s
g
n
{
(
x
−
x
r
)
c
o
s
φ
}
\varphi=\psi_r-\phi_{T_{ar}}, s_r=sgn\{(x-x_r)cos\varphi\}
φ=ψr−ϕTar,sr=sgn{(x−xr)cosφ} 。由于我们知道跟踪区域的边界,因此可以用跟踪范围内任意的
X
X
X 值代替
x
x
x 来计算符号
s
r
s_r
sr。
Y
Y
Y 边界上接收者的解与上式方程组解对偶,为简便起见省略。
在实践中,监测区域周围可能存在多个接收器。为了充分利用室内
W
i
−
F
i
Wi-Fi
Wi−Fi 基础设施,我们进一步融合多个
R
R
R 接收器的定位结果:
l
=
∑
i
=
1
R
u
i
l
i
l=\sum^R_{i=1}u_il_i
l=i=1∑Ruili
其中
u
i
u_i
ui 第
i
i
i 个接收机位置估计的权重。观察到较大的
D
F
S
DFS
DFS
f
D
f_D
fD 会导致更精确的位置估计,作者启发式地分配权重:
u
i
=
1
+
∣
f
D
i
∣
R
+
∑
i
=
1
R
∣
f
D
i
∣
u_i=\frac{1+|f_{D_i}|}{R+\sum^R_{i=1}|f_{D_i}|}
ui=R+∑i=1R∣fDi∣1+∣fDi∣
***note:此集成步骤仅用于实际考虑,以便在有多个接收器可用的情况下进一步改进。"Widar2.0"本身只需要一个链接就可以很好地工作。
5 EVALUATION
5.1 Experiment Methodology
Implementation. 作者使用一对配备英特尔
5300
5300
5300网卡的现成笔记本电脑实现“Widar2.0”。发射机有一个天线,向空中广播数据包。接收器有三个天线,形成一个统一的线性阵列。
L
i
n
u
x
Linux
Linux
802.11
n
802.11n
802.11n
C
S
I
CSI
CSI
T
o
o
l
Tool
Tool安装在设备中,用于收集
C
S
I
CSI
CSI 数据。设备被设置为在监视器模式下工作,在
165
165
165频道上
5.825
G
H
z
5.825 GHz
5.825GHz。设置报文传输速率为
1000
H
z
1000 Hz
1000Hz。处理计算机采用
I
n
t
e
l
Intel
Intel
i
7
−
7700
i7-7700
i7−7700
3.6
G
H
z
3.6GHz
3.6GHz
C
P
U
CPU
CPU,使用
M
A
T
L
A
B
MATLAB
MATLAB 处理
C
S
I
CSI
CSI 数据。
Evaluation setup. 为了充分评估"Widar2.0"的性能,我们在
3
3
3 个室内环境中进行了实验:一个大的空教室,一个小的办公室和一个狭窄的走廊。
f
i
g
u
r
e
9
figure9
figure9 显示了不同场景中设备和跟踪区域的部署。特别是,在教室场景中,我们部署了一个额外的接收器来演示"Widar2.0"在存在多个设备的情况下的性能。这两条链路彼此正交。
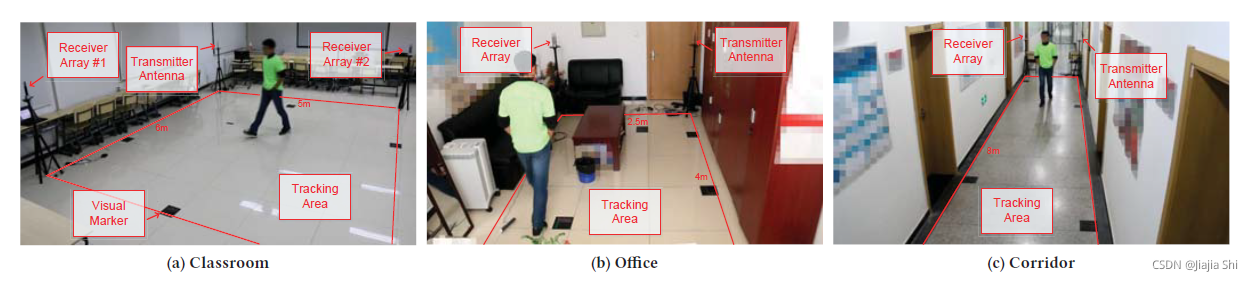
共有
6
6
6 名志愿者(
4
4
4 男
2
2
2 女)参与实验,沿着直线、矩形、圆形等不同形状的轨迹行走。
f
i
g
u
r
e
10
figure10
figure10 显示了"Widar2.0"的跟踪结果示例。代码和数据样本参考官方网站 Widar2.0Project.zip.
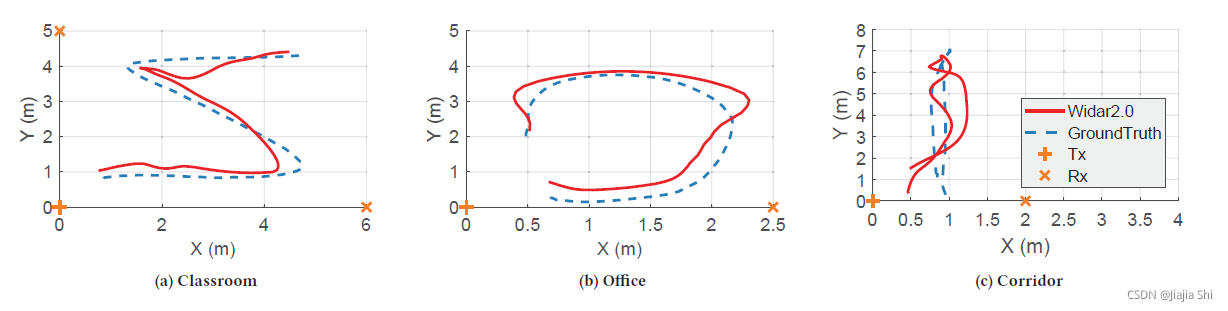
Ground truth. 作者通过基于视频的跟踪解决方案获得"ground truth"。具体来说,安装了一个数码相机来拍摄步行视频。同时,志愿者们被要求穿一件浅绿色的
T
T
T 恤,以便于识别和跟踪。跟踪过程首先利用视场中的标记点计算像素帧与世界帧之间的投影矩阵。然后,在目标点高度不变的情况下,将目标点的像素位置转换为现实世界中的水平
2
D
2D
2D 位置。
5.2 System Performance
Localization accuracy. 作者首先报告"Widar2.0"的总体性能。如
f
i
g
u
r
e
11
figure11
figure11 所示,"Widar2.0"在只有一个
W
i
−
F
i
Wi-Fi
Wi−Fi 链路的情况下,平均定位误差为
0.75
m
0.75 m
0.75m。相比之下,使用两个链路可以提高性能,平均定位误差为
0.63
0.63
0.63 m。性能的提高不仅是因为测量的量的增加,还因为两个链接的正交部署。具体来说,在
C
S
I
CSI
CSI 标定过程中,通过两条正交链路,至少有一条链路能够捕获到足够大的
D
F
S
DFS
DFS 反射信号,从而可以通过带通滤波器清晰地提取反射信号(
S
e
c
t
i
o
n
3.3
Section 3.3
Section3.3)。注意到目标的行走方向确实会影响系统性能,作者将在
S
e
c
t
i
o
n
5.3
Section 5.3
Section5.3 进一步分析其影响。
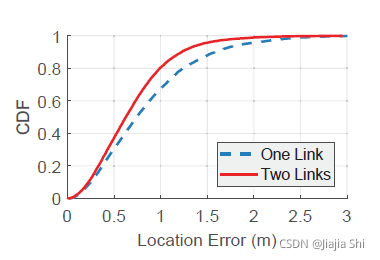
Comparative study. 作者比较了"Widar2.0"与最先进的"DynamicMusic"和"IndoTrack"。"DynamicMusic"使用
J
A
D
E
JADE
JADE 估计目标在接收机上反映的信号的
A
o
A
s
AoAs
AoAs,并将
A
o
A
s
AoAs
AoAs 的交点定位为目标位置。"IndoTrack"进一步将
D
F
S
DFS
DFS 与
A
o
A
AoA
AoA 合并用于跟踪。该算法通过瞬时
D
F
S
DFS
DFS 和目标位置递归计算目标速度,然后用新估计的目标速度更新目标位置。同时,利用
A
o
A
AoA
AoA 来定位目标的初始位置,并计算由
D
F
S
DFS
DFS 计算出的轨迹的置信度。"DynamicMusic"和"IndoTrack"都直接从
C
S
I
CSI
CSI 估计反射信号的
A
o
A
AoA
AoA,但由于目标远离链路,不能得到稳定的
A
o
A
AoA
AoA 估计。作为一种替代方法,作者使用由"Widar2.0"估算的
A
o
A
s
AoAs
AoAs 作为这两种方法的输入。
f
i
g
u
r
e
12
figure12
figure12 显示了三种方法的系统性能。首先,"Widar2.0"明显优于"DynamicMusic",后者的平均定位偏差为
1.1
m
1.1 m
1.1m。这主要是因为"DynamicMusic"只使用
A
o
A
AoA
AoA,无法用
D
F
S
DFS
DFS 表示的运动连续性来补偿
A
o
A
AoA
AoA 错误。此外,"DynamicMusic"无法在两个接收器之间的
L
o
S
LoS
LoS 路径上精确定位目标。在这种条件恶劣的情况下,两个接收机上的
A
o
A
AoA
AoA 重合,点与点相交扩展成为长线段,定位误差大。
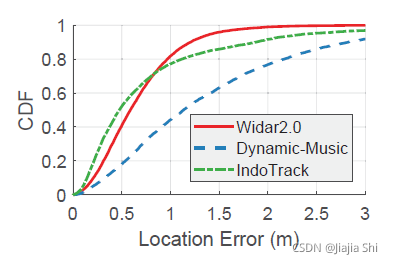
其次,"Widar2.0"的平均性能略低于"IndoTrack",但仍可与之媲美,"IndoTrack"的平均定位误差为
0.48
m
0.48 m
0.48m。然而,"IndoTrack"的“错误尾(error tail)”比"Widar2.0"长得多。原因是"IndoTrack"仅利用
D
F
S
DFS
DFS 进行直接跟踪,而使用
A
o
A
AoA
AoA 作为估计跟踪的指标。因此,虽然"IndoTrack"在跟踪开始时得益于运动连续性,但随着
D
F
S
DFS
DFS 误差的累积,其性能逐渐下降。而"Widar2.0"同时使用了由
D
F
S
DFS
DFS 校准的
A
o
A
AoA
AoA 和
T
o
F
ToF
ToF 进行跟踪,避免了误差积累。
S
e
c
t
i
o
n
5.3
Section 5.3
Section5.3 进一步分析了步行距离的影响。
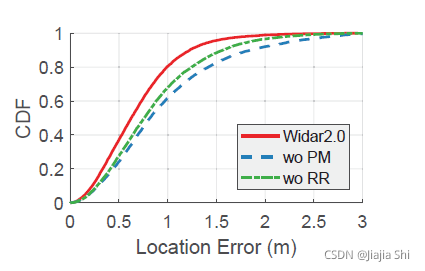
Benefits of individual modules. 本部分研究了所提出的“路径匹配(PM)”和“范围细化(RP)”过程对系统性能的影响。
f
i
g
u
r
e
13
figure13
figure13 显示了这两个步骤的效果。一方面,没有
P
M
PM
PM 过程,平均定位误差增加到
0.84
m
0.84 m
0.84m;结果表明,与"Hungarian algorithm"相比,
P
M
PM
PM 过程对估计噪声具有更强的鲁棒性,能够更准确地匹配感兴趣的信号参数。另一方面,通过
R
P
RP
RP 过程,跟踪精度提高了
13
c
m
13 cm
13cm。具体来说,
R
P
RP
RP 过程用
D
F
S
DFS
DFS 平滑基于
T
o
F
ToF
ToF 的距离,从而受益于目标移动的连续性。
5.3 Parameter Study
Impact of walking direction. 为了评估行走方向对系统性能的影响,作者要求志愿者沿着不同方向的直线行走,并通过单链接和两个正交链接跟踪他们的位置。 f i g u r e 14 figure14 figure14 显示了随行走方向的定位误差分布。具体来说,在单链路情况下,目标趋于与链路并行行走,接收机观测到的反射信号 D F S DFS DFS 变小,标定过程性能下降,定位误差统计增加相比之下,添加链接的性能提升来自两个方面。
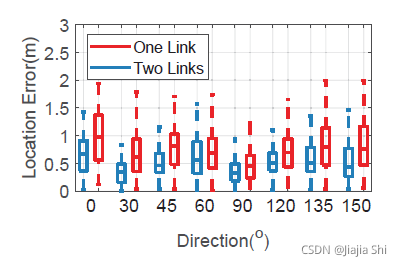
首先,由于该系统对来自多个接收机测量的噪声具有更强的鲁棒性,从而降低了各个行走方向的定位误差水平。其次,沿行走方向的误差分布更加均匀,通过两个链路可以捕获到 D F S DFS DFS 显著的信号,从而使信号参数的估计更加准确。
Impact of walking distance. 作者进一步探索了行走距离的影响。他们要求志愿者保持在监测区域距离约
40
40
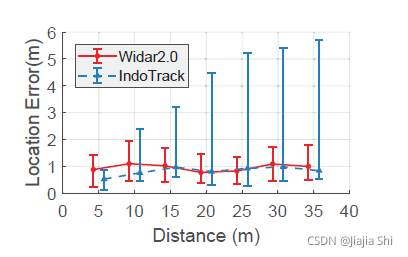
40 m,并利用采集的痕迹对"Widar2.0"和"IndoTrack"两种方法进行评价。
f
i
g
u
r
e
15
figure15
figure15 显示了两种方法的平均本地化错误。错误条表示
10
10%
10 和
90
90%
90 的错误边界。如图所示,虽然"IndoTrack"在行走距离较短时定位误差较小,但随着距离的增加,其定位结果发生漂移。原因是"IndoTrack"仅使用
D
F
S
DFS
DFS 来估计目标速度并进一步更新目标位置,存在
D
F
S
DFS
DFS 误差累积的问题。而"Widar2.0"采用了绝对
T
o
F
ToF
ToF,避免了误差积累,实现了一致的定位精度,对于连续跟踪是可行的。
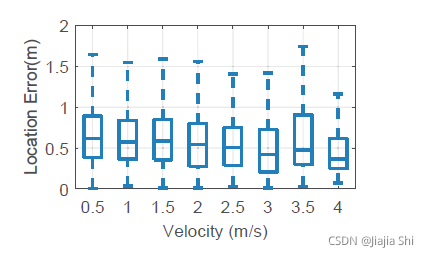
Impact of walking velocity. 在实验中,志愿者被允许以不同的速度自由行走。为了评估行走速度的影响,作者从数码相机捕捉的“ground truth”位置计算地面真实速度。
f
i
g
u
r
e
16
figure16
figure16 给出了位置误差随行走速度的分布。一般情况下,人的行走速度不超过
4
m
/
s
4m/s
4m/s。如图所示,定位误差稳定在
0.6
m
0.6 m
0.6m 左右,但随着行走速度的增加,定位误差逐渐减小。观测直观,行走速度大导致接收机
D
F
S
DFS
DFS 大,便于标定过程提取反射信号。
Impact of environment. 为了展示环境多样性的影响,我们在教室、办公室和走廊三个不同的场景中进行了实验,如
f
i
g
u
r
e
9
figure9
figure9 所示。注意两个接收器在教室使用,而一个接收器在办公室和走廊使用。
f
i
g
u
r
e
17
figure17
figure17 显示了"Widar2.0"在不同位置的本地化错误。如图所示,"Widar2.0"的平均定位误差较低,分别为
0.63
m
0.63 m
0.63m、
0.4
m
0.4 m
0.4m 和
0.51
m
0.51 m
0.51m。由于"Widar2.0"仅依赖非零
D
F
S
DFS
DFS 的反射信号和占主导地位的
L
o
S
LoS
LoS 信号,因此对室内环境中的多径效应具有鲁棒性,适用于各种室内环境。
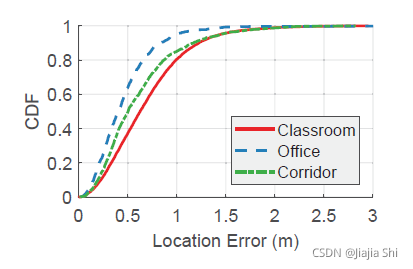
但是,系统的性能在不同的环境中仍然存在差异,这是由两个因素造成的。首先,系统性能与跟踪区域的大小成反比。具体来说,教室、办公室和走廊的跟踪面积分别为 30 m 2 30m^2 30m2、 10 m 2 10m^2 10m2 和 20 m 2 20m^2 20m2。跟踪区域越大,目标反射的信号越弱,越容易受到噪声的影响,导致系统性能下降。
其次,发射机和接收机之间的距离(即链路长度)也会影响系统的性能。在给定目标行走方向和速度的情况下,链路长度越大,接收机处 D F S DFS DFS 越小,会降低系统性能。具体来说,教室( 6 m 6m 6m)的链接长度远远大于办公室( 2.5 m 2.5 m 2.5m)和走廊( 2 m 2 m 2m),这就解释了大型教室中系统性能下降的原因。
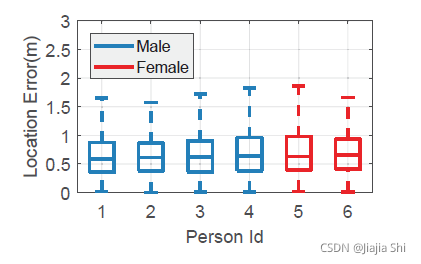
Impact of human diversity. 为了确定"Widar2.0"是否始终适用于不同的用户,作者招募了
6
6
6 名志愿者,他们的性别、身高和体型都不同。实验前,只向志愿者解释基本的实验设置,如跟踪区域和典型的行走轨迹。他们没有经过专门训练,按照自己的习惯走路。
f
i
g
u
r
e
18
figure18
figure18 绘制了不同目标下"Widar2.0"的定位错误。如图所示,"Widar2.0"在不知道目标的任何身体特征的情况下,在所有目标上实现了一致的定位精度。
Impact of packet rate. 为了找出"Widar2.0"正确工作所需的最小包速率,我们在发射机初始化包速率为
1000
H
z
1000 Hz
1000Hz,并逐渐丢弃
C
S
I
CSI
CSI 收集,以达到
500
H
z
500 Hz
500Hz 和
250
H
z
250 Hz
250Hz 的包速率。
f
i
g
u
r
e
19
figure19
figure19 显示了不同包速率的本地化错误(蓝色条)。当包速率从
1000
H
z
1000 Hz
1000Hz 指数级下降到
250
H
z
250 Hz
250Hz时,基本保持不变。它演示了"Widar2.0"工作在中等包速率,并适用于真实的
W
i
−
F
i
Wi-Fi
Wi−Fi 传输。但是,进一步降低包速率可能会导致
D
F
S
DFS
DFS 估计的混叠。具体来说,当人体行走速度不超过
5
m
/
s
5 m/s
5m/s 时,相应的
D
F
S
DFS
DFS 范围在
±
f
D
m
a
x
=
±
100
H
z
±f_{D_max} =±100 Hz
±fDmax=±100Hz 之内。假设数据包以
Δ
t
\Delta_t
Δt 的间隔均匀传输,为了唯一确定
D
F
S
DFS
DFS,原子“DFS诱发相位(atomic DFS-induced phase)”
2
π
f
D
Δ
t
2\pi f_D\Delta _t
2πfDΔt应该在
2
π
2\pi
2π 的范围内。因此,"Widar2.0"所需的最大数据包间隔为
Δ
t
m
a
x
=
1
2
f
D
m
a
x
\Delta _{t_{max}}=\frac{1}{2f_{D_{max}}}
Δtmax=2fDmax1,对应最小包数速率约
200
H
z
200 Hz
200Hz。
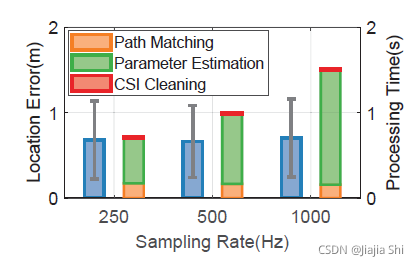
作者进一步评估"Widar2.0"中步骤的每秒计算成本,如
f
i
g
u
r
e
19
figure19
figure19 所示。由于范围细化和定位步骤花费的时间小于
1
m
s
1 ms
1ms,我们只考虑其余步骤的处理时间,即
C
S
I
CSI
CSI 清洗、参数估计和路径匹配。如图所示,参数估计这一步主要的时间开销来自于迭代优化。通过降低传输速率,降低了计算成本。考虑到
250
H
z
250 Hz
250Hz 的传输速率就足够了,每秒的处理时间是
0.7
s
0.7 s
0.7s,因此可以使用"Widar2.0"进行实时跟踪。
6 DISCUSSION
Multiple person tracking. 作者进行了初步实验,两个人在监测区域行走。结果表明,虽然"Widar2.0"能够准确估计
D
F
S
DFS
DFS 并识别两个人,但不能准确获得
A
o
A
AoA
AoA 和
T
o
F
ToF
ToF,不能进一步跟踪多个人。原因有两方面。首先,
N
I
C
NIC
NIC 只有
3
3
3 个天线,限制了
A
o
A
AoA
AoA 的分辨率,以分离两个反射路径。其次,信道带宽只有
20
M
H
z
20 MHz
20MHz,导致
T
o
F
ToF
ToF 相位变化小,
T
o
F
ToF
ToF 估计错误。在修订中,作者计划在一个接收器上组合多个
W
i
−
F
i
Wi-Fi
Wi−Fi 网卡,并拼接多个通道,用于细粒度的
A
o
A
AoA
AoA 和
T
o
F
ToF
ToF 估计,用于多人跟踪。
Tracking in NLoS condition. 要使用"Widar2.0"启用跟踪,需要满足两种类型的
L
o
S
LoS
LoS 条件。首先,任何收发器和人之间的
L
o
S
LoS
LoS路径都应该存在,因为"Widar2.0"需要定位时人直接反映的信号的
T
o
F
ToF
ToF(
S
e
c
t
i
o
n
4.3
Section 4.3
Section4.3)。其次,两个收发器之间的LoS路径应该存在,因为"Widar2.0"只能估计链路反射信号与最强
L
o
S
LoS
LoS 信号之间的
T
o
F
s
ToFs
ToFs 差值(
S
e
c
t
i
o
n
3.3
Section 3.3
Section3.3)。在不满足
L
o
S
LoS
LoS 条件的情况下。
T
o
F
ToF
ToF 估计错误,不能使用。但是,由于典型室内环境中存在多个链路,它可以对这些链路的跟踪结果进行分组,滤除
N
L
o
S
NLoS
NLoS 条件下的离群值。
Device deployment. 器件的位移是限制"Widar2.0"跟踪范围的主要因素。一方面,反射信号比
L
o
S
LoS
LoS 信号弱得多,因为其传播距离较长,反射损耗增加,在
C
S
I
CSI
CSI 中很难捕捉到。因此,它很可能会移动人体高度周围的设备,以增加反射表面。另一方面。"Widar2.0"通过其非零
D
F
S
DFS
DFS 识别反射信号。相当于反射路径长度的变化率。但是,增加收发机之间的距离会降低变化率,使反射信号和静态信号更难区分。因此,连杆长度应控制在适度范围内,通过实验验证为
6
m
6 m
6m。
7 RELATED WORK
团队的工作与无线传感的研究广泛相关,研究射频信道特性,并导出语法( e . g . e.g. e.g. 位置、速度)和语义( e . g . e.g. e.g. 人类活动)环境上下文。
8 CONCLUSION
在本文中,作者提出了"Widar2.0"——第一个无源跟踪系统,只需要一个单一的
W
i
−
F
i
Wi-Fi
Wi−Fi 链路,达到亚米级跟踪精度,不支持任何额外的基础设施或传感器。作者在
C
O
T
S
W
i
−
F
i
COTS Wi-Fi
COTSWi−Fi 设备上实现和评估"Widar2.0"。结果表明,"Widar2.0"在
6
m
×
5
m
6 m × 5 m
6m×5m 的区域内实现了
0.75
m
0.75 m
0.75m 的中值定位精度,可与基于多个链接的最先进方法相媲美。"Widar2.0"为那些可用或可访问设备较少的新应用程序(
e
.
g
.
e.g.
e.g. 家庭和移动环境)打开了被动跟踪。未来的工作将扩展到多目标跟踪和穿壁监测。
REFERENCES
[1] CCCF专栏丨AIoT时代的智能无线感知:特征、算法、数据集.
[2] Widar2.0: Passive Human Tracking with a Single Wi-Fi Link.








 本文介绍了一种名为Widar2.0的无线感知系统,它利用单个Wi-Fi链路实现被动式人类跟踪和定位,无需额外传感器。通过CSI-MotionModel和参数联合估计,系统克服了多路径信号挑战,实现了厘米级精度。文章详细阐述了关键技术如 CSI 清洗、路径匹配和定位框架,以及性能评估和局限性讨论。
本文介绍了一种名为Widar2.0的无线感知系统,它利用单个Wi-Fi链路实现被动式人类跟踪和定位,无需额外传感器。通过CSI-MotionModel和参数联合估计,系统克服了多路径信号挑战,实现了厘米级精度。文章详细阐述了关键技术如 CSI 清洗、路径匹配和定位框架,以及性能评估和局限性讨论。
















 2718
2718

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








