引言:
来考虑一个问题,
平面上6个点,A,B,C,D,E,F,假定已知其中一些点之间的距离,
现在,要求A到其它5个点,B,C,D,E,F各点的最短距离。
如下图所示:
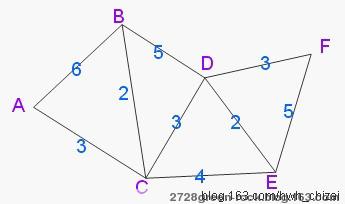
经过上图,我们可以轻而易举的得到A->B,C,D,E,F各点的最短距离:
目的 路径 最短距离
A=>A, A->A 0
A=>B, A->C->B 3+2=5
A=>C, A->C 3
A=>D, A->C->D 3+3=6
A=>E, A->C->E 3+4=7
A=>F, A->C->D->F 3+3+3=9
我想,如果是单单出上述一道填空题,要你答出A->B,C,D,E,F各点的最短距离,
一个小学生,掰掰手指,也能在几分钟之内,填写出来。
我们的问题,当然不是这么简单,上述只是一个具体化的例子而已。
实际上,很多的问题,如求图的最短路径问题,就要用到上述方法,不断比较、不断寻找,以期找到最短距离的路径,此类问题,便是Dijkstra 算法的应用了。当然,还有BFS算法,以及更高效的A*搜寻算法。
A*搜寻算法已在本BLOG内有所详细的介绍,本文咱们结合fibonacci堆实现Dijkstra 算法。
即,Dijkstra + fibonacci堆 c实现。
我想了下,把一个算法研究够透彻之后,还要编写代码去实现它,才叫真正掌握了一个算法。本BLOG内经典算法研究系列,已经写了18篇文章,十一个算法,所以,还有10多个算法,待我去实现。
代码风格
实现一个算法,首先要了解此算法的原理,了解此算法的原理之后,便是写代码实现。
在打开编译器之前,我先到网上搜索了一下“Dijkstra 算法+fibonacci堆实现”。
发现:网上竟没有过 Dijkstra + fibonacci堆实现的c代码,而且如果是以下几类的代码,我是直接跳过不看的:
1、没有注释(看不懂)。
2、没有排版(不舒服)。
3、冗余繁杂(看着烦躁)。
fibonacci堆实现Dijkstra 算法
ok,闲话少说,咱们切入正题。下面,咱们来一步一步利用fibonacci堆实现Dijkstra 算法吧。
前面说了,要实现一个算法,首先得明确其算法原理及思想,而要理解一个算法的原理,又得知道发明此算法的目的是什么,即,此算法是用来干什么的?
由前面的例子,我们可以总结出:Dijkstra 算法是为了解决一个点到其它点最短距离的问题。
我们总是要找源点到各个目标点的最短距离,在寻路过程中,如果新发现了一个新的点,发现当源点到达前一个目的点路径通过新发现的点时,路径可以缩短,那么我们就必须及时更新此最短距离。
ok,举个例子:如我们最初找到一条路径,A->B,这条路径的最短距离为6,后来找到了C点,发现若A->C->B点路径时,A->B的最短距离为5,小于之前找到的最短距离6,所以,便得此更新A到B的最短距离:为5,最短路径为A->C->B.
好的,明白了此算法是干什么的,那么咱们先用伪代码尝试写一下吧(有的人可能会说,不是吧,我现在,什么都还没搞懂,就要我写代码了。额,你手头不是有资料么,如果全部所有的工作,都要自己来做的话,那就是一个浩大的工程了。:D。)。
咱们先从算法导论上,找来Dijkstra 算法的伪代码如下:

1 DIJKSTRA(G, w, s) 2 INITIALIZE-SINGLE-SOURCE(G, s) //1、初始化结点工作 3 S ← 4 Q ← V[G] //2、插入结点操作 5 while Q ≠ 6 do u ← EXTRACT-MIN(Q) //3、从最小队列中,抽取最小点工作 7 S ← S ∪{u} 8 for each vertex v ∈ Adj[u] 9 do RELAX(u, v, w) //4、松弛操作。
伪代码毕竟与能在机子上编译运行的代码不同,还有很多工作要做。
首先,咱们看一下上述伪代码,可以看出,基本上,此Dijkstra 算法主要分为以下四个步骤:
1、初始化结点工作
2、插入结点操作
3、从最小队列中,抽取最小点工作
4、松弛操作。
ok,由于第2个操作涉及到斐波那契堆,比较复杂一点,咱们先来具体分析第1、2、4个操作:
1、得用O(V)的时间,来对最短路径的估计,和对前驱进行初始化工作。

1 INITIALIZE-SINGLE-SOURCE(G, s) 2 for each vertex v ∈ V[G] 3 do d[v] ← ∞ 4 π[v] ← NIL //O(V) 5 d[s] 0
我们根据上述伪代码,不难写出以下的代码:

1 void init_single_source(Graph *G,int s) 2 { 3 for (int i=0;i<G->n;i++) { 4 d[i]=INF; 5 pre[i]=-1; 6 } 7 d[s]=0; 8 }
2、插入结点到队列的操作
2 S ←
3 Q ← V[G] //2、插入结点操作
代码:

1 for (i=0;i<G->n;i++) 2 S[i]=0;
4、松弛操作。
首先得理解什么是松弛操作:
Dijkstra 算法使用了松弛技术,对每个顶点v<-V,都设置一个属性d[v],用来描述从源点s到v的最短路径上权值的上界,称为最短路径的估计。

RELAX(u, v, w) 1 if d[v] > d[u] + w(u, v) 2 then d[v] ← d[u] + w(u, v) 3 π[v] ← u //O(E)
同样,我们不难写出下述代码:

1 void relax(int u,int v,Graph *G) 2 { 3 if (d[v]>d[u]+G->w[u][v]) 4 { 5 d[v] = d[u]+G->w[u][v]; //更新此最短距离 6 pre[v]=u; //u为v的父结点 7 } 8 }
再解释一下上述relax的代码,其中u为v的父母结点,当发现其父结点d[u]加上经过路径的距离G->w[u][v],小于子结点到源点的距离d[v],便得更新此最短距离。
请注意,说的明白点:就是本来最初A到B的路径为A->B,现在发现,当A经过C到达B时,此路径距离比A->B更短,当然,便得更新此A到B的最短路径了,即是:A->C->B,C 即成为了B的父结点(如此解释,我相信您已经明朗。:D。)。
即A=>B <== A->C->B,执行赋值操作。
ok,第1、2、4个操作步骤,咱们都已经写代码实现了,那么,接下来,咱们来编写第3个操作的代码:3、从最小队列中,抽取最小点工作。
相信,你已经看出来了,我们需要构造一个最小优先队列,那用什么来构造最小优先队列列?对了,堆。什么堆最好,效率最高,呵呵,就是本文要实现的fibonacci堆。
为什么?ok,请看最小优先队列的三种实现方法比较:

EXTRACT-MIN + RELAX I、 简单方式: O(V*V + E*1) II、 二叉/项堆: O(V*lgV + |E|*lgV) 源点可达:O(E*lgV) 稀疏图时,有E=o(V^2/lgV), => O(V^2) III、斐波那契堆:O(V*lgV + E)
其中,V为顶点,E为边。好的,这样我们就知道了:Dijkstra 算法中,当用斐波纳契堆作优先队列时,算法时间复杂度为O(V*lgV + E)。
额,那么接下来,咱们要做的是什么列?当然是要实现一个fibonacci堆了。可要怎么实现它,才能用到我们
Dijkstra 算法中列?对了,写成一个库的形式。库?呵呵,是一个类。
ok,以下就是这个fibonacci堆的实现:

1 //:priorityqueue.h文件,外部参数说明 2 #include <vector> 3 #ifndef HEAP_DEF_RICKONE_20061123 4 #define HEAP_DEF_RICKONE_20061123 5 namespace Heap 6 { 7 //Binary Heap 8 template <class T> 9 class BinaryHeap 10 { 11 std::vector<T> h; 12 int n; 13 public: 14 BinaryHeap(); 15 void max_heapify(int i); 16 void min_heapify(int i); 17 void insert(const T &e); 18 T minnum() const; 19 T extract_min(); 20 void decrease_key(int x,const T &k); 21 void kill(int x); 22 }; 23 //Fibonacci Heap 24 template <class T> 25 class FibonacciHeap 26 { 27 enum{NEGATIVE_INFINITY=1985}; 28 struct fibnode 29 { 30 T data; 31 fibnode *p,*child,*left,*right; 32 int degree; 33 bool mark; 34 } *min; 35 unsigned long int n; 36 public: 37 FibonacciHeap();//Construct a Heap 38 ~FibonacciHeap(); 39 const fibnode* insert(const T &e); 40 T minnum() const; 41 T extract_min(); 42 void decrease_key(const fibnode *x,const T &k,int TAG=0); 43 void kill(const fibnode *x); 44 void heap_union(FibonacciHeap<T> &h); 45 //for test 46 void Display(); 47 void Print(int depth,fibnode *x); 48 private: 49 void release(fibnode *x); 50 void remove(fibnode *x); 51 void dblist_union(fibnode *a,fibnode *b); 52 void consolidate(); 53 void cut(fibnode *x,fibnode *y); 54 void cascading_cut(fibnode *y); 55 }; 56 } 57 #endif 58 //:binaryheap.h BinaryHeap实现 59 #include "priorityqueue.h" 60 template <class T> 61 Heap::BinaryHeap<T>::BinaryHeap() 62 { 63 h.push_back(T()); 64 n=1; 65 } 66 template <class T> 67 void Heap::BinaryHeap<T>::max_heapify(int i) 68 { 69 //float up 70 for(;i>1;) 71 { 72 int p=i/2; 73 if(h[i]<h[p]) 74 { 75 T temp(h[i]); 76 h[i]=h[p]; 77 h[p]=temp; 78 i=p; 79 } 80 else 81 break; 82 } 83 } 84 template <class T> 85 void Heap::BinaryHeap<T>::min_heapify(int i) 86 { 87 //float down 88 if(i<1 || i>=n) 89 return; 90 for(;;) 91 { 92 int left=i*2; 93 int right=left+1; 94 int smallest; 95 if(left>=n) 96 break; 97 if(right>=n) 98 smallest=left; 99 else 100 { 101 if(h[left]<h[right]) 102 smallest=left; 103 else 104 smallest=right; 105 } 106 if(h[smallest]<h[i]) 107 { 108 T temp(h[i]); 109 h[i]=h[smallest]; 110 h[smallest]=temp; 111 i=smallest; 112 } 113 else 114 break; 115 } 116 } 117 template <class T> 118 void Heap::BinaryHeap<T>::insert(const T &e) 119 { 120 if(n>=h.size()) 121 h.push_back(e); 122 else 123 h[n]=e; 124 n++; 125 max_heapify(n-1); 126 } 127 template <class T> 128 T Heap::BinaryHeap<T>::minnum() const 129 { 130 if(n>1) 131 return h[1]; 132 return T(); 133 } 134 template <class T> 135 void Heap::BinaryHeap<T>::decrease_key(int x,const T &k) 136 { 137 if(h[x]<k) 138 { 139 //error warning 140 return; 141 } 142 h[x]=k; 143 max_heapify(x); 144 } 145 template <class T> 146 void Heap::BinaryHeap<T>::kill(int x) 147 { 148 if(x>=1 && x<n) 149 { 150 h[x]=h[n-1]; 151 min_heapify(x); 152 n--; 153 } 154 } 155 template <class T> 156 T Heap::BinaryHeap<T>::extract_min() 157 { 158 if(n>1) 159 { 160 T min=h[1]; 161 kill(1); 162 return min; 163 } 164 return h[0]; 165 } 166 //:fibonacciheap.h FibonacciHeap实现 167 //中间包括一些原用于测试的代码,可去掉 168 #include "priorityqueue.h" 169 template <class T> 170 Heap::FibonacciHeap<T>::FibonacciHeap() 171 { 172 min=NULL; 173 n=0; 174 } 175 template <class T> 176 void Heap::FibonacciHeap<T>::release(fibnode *x) 177 { 178 if(x==NULL) 179 return; 180 fibnode *p=x,*q; 181 do 182 { 183 q=p; 184 p=p->right; 185 release(q->child); 186 } 187 while(p!=x); 188 do 189 { 190 q=p; 191 p=p->right; 192 //printf("deleting %d ...\n",q->data); 193 delete q; 194 } 195 while(p!=x); 196 } 197 template <class T> 198 Heap::FibonacciHeap<T>::~FibonacciHeap() 199 { 200 release(min); 201 } 202 template <class T> 203 void Heap::FibonacciHeap<T>::remove(fibnode *x) 204 { 205 if(x==NULL) 206 return; 207 fibnode *l,*r; 208 l=x->left; 209 r=x->right; 210 l->right=r; 211 r->left=l; 212 x->left=x; 213 x->right=x; 214 } 215 template <class T> 216 void Heap::FibonacciHeap<T>::dblist_union(fibnode *a,fibnode *b) 217 { 218 if(a==NULL || b==NULL) 219 return; 220 fibnode *al=a->left,*bl=b->left; 221 al->right=b; 222 a->left=bl; 223 bl->right=a; 224 b->left=al; 225 } 226 template <class T> 227 const Heap::FibonacciHeap<T>::fibnode* Heap::FibonacciHeap<T>::insert(const T &e) 228 { 229 fibnode *x=new fibnode; 230 x->degree=0; 231 x->p=NULL; 232 x->child=NULL; 233 x->left=x; 234 x->right=x; 235 x->mark=false; 236 x->data=e; 237 if(min==NULL) 238 min=x; 239 else 240 dblist_union(min,x); 241 if(e<min->data) 242 min=x; 243 ++n; 244 return (const fibnode*)x; 245 } 246 template <class T> 247 T Heap::FibonacciHeap<T>::minnum() const 248 { 249 if(min==NULL) 250 return T(); 251 return min->data; 252 } 253 template <class T> 254 void Heap::FibonacciHeap<T>::heap_union(FibonacciHeap<T> &h) 255 { 256 dblist_union(min,h.min); 257 if(min==NULL || (h.min !=NULL && h.min->data < min->data)) 258 min=h.min; 259 n+=h.n; 260 h.min=NULL; 261 } 262 template <class T> 263 void Heap::FibonacciHeap<T>::consolidate() 264 { 265 fibnode *A[32]={NULL}; 266 fibnode *w=min; 267 do 268 { 269 fibnode *x=w; 270 w=w->right; 271 int d=x->degree; 272 while(A[d]!=NULL) 273 { 274 fibnode *y=A[d]; 275 if(y->data < x->data) 276 { 277 fibnode *tmp=x; 278 x=y; 279 y=tmp; 280 } 281 // 282 if(y==min) 283 { 284 if(w==min) 285 w=min->right; 286 min=min->right; 287 } 288 remove(y); 289 if(x->child==NULL) 290 x->child=y; 291 else 292 dblist_union(x->child,y); 293 y->p=x; 294 x->degree++; 295 y->mark=false; 296 A[d]=NULL; 297 d++; 298 } 299 A[d]=x; 300 } 301 while(w!=min); 302 for(int i=0;i<32;++i) 303 { 304 if(A[i]!=NULL) 305 { 306 if(A[i]->data < min->data) 307 min=A[i]; 308 } 309 } 310 } 311 template <class T> 312 T Heap::FibonacciHeap<T>::extract_min() 313 { 314 if(min==NULL) 315 return T(); 316 T z=min->data; 317 fibnode *x=min->child; 318 if(x!=NULL) 319 { 320 while(x->right!=min->child) 321 { 322 x->p=NULL; 323 x=x->right; 324 } 325 x->p=NULL; 326 } 327 //add each child of z to the root list 328 dblist_union(min,min->child); 329 //remove z from the root list 330 fibnode *r=min->right; 331 remove(min); 332 // 333 if(r==min) 334 { 335 delete min; 336 min=NULL; 337 } 338 else 339 { 340 delete min; 341 min=r; 342 consolidate(); 343 } 344 --n; 345 return z; 346 } 347 template <class T> 348 void Heap::FibonacciHeap<T>::cut(fibnode *x,fibnode *y) 349 { 350 if(y->child==x) 351 { 352 if(x->right==x) 353 y->child=NULL; 354 else 355 y->child=x->right; 356 } 357 remove(x); 358 y->degree--; 359 dblist_union(min,x); 360 x->p=NULL; 361 x->mark=false; 362 } 363 template <class T> 364 void Heap::FibonacciHeap<T>::cascading_cut(fibnode *y) 365 { 366 fibnode *z=y->p; 367 if(z!=NULL) 368 { 369 if(y->mark==false) 370 y->mark=true; 371 else 372 { 373 cut(y,z); 374 cascading_cut(z); 375 } 376 } 377 } 378 template <class T> 379 void Heap::FibonacciHeap<T>::decrease_key(const fibnode *cx,const T &k,int TAG) 380 { 381 fibnode *x=(fibnode*)cx,*y=x->p; 382 if(x->data < k) 383 return;//error "new key is greater than current key x" 384 x->data=k; 385 if(y!=NULL && (TAG==NEGATIVE_INFINITY || (x->data < y->data))) 386 { 387 cut(x,y); 388 cascading_cut(y); 389 } 390 if(TAG==NEGATIVE_INFINITY || x->data < min->data) 391 min=x; 392 } 393 template <class T> 394 void Heap::FibonacciHeap<T>::kill(const fibnode *cx) 395 { 396 decrease_key(cx,T(),NEGATIVE_INFINITY); 397 extract_min(); 398 } 399 400 //------------------------------FOR TEST---------------------------- 401 template <class T> 402 void Heap::FibonacciHeap<T>::Display() 403 { 404 Print(0,min); 405 } 406 template <class T> 407 void Heap::FibonacciHeap<T>::Print(int depth,fibnode *x) 408 { 409 int i; 410 if(x==NULL) 411 { 412 for(i=0;i<depth;++i) 413 printf(" "); 414 printf("-\n"); 415 return; 416 } 417 fibnode *p=x,*q; 418 do 419 { 420 q=p; 421 p=p->right; 422 for(i=0;i<depth;++i) 423 printf(" "); 424 printf("<%d> degree=%d\n",q->data,q->degree); 425 Print(depth+1,q->child); 426 } 427 while(p!=x); 428 } 429 //:test.cpp 测试与使用 430 #include "binaryheap.h" 431 #include "fibonacciheap.h" 432 int main(void) 433 { 434 Heap::FibonacciHeap<int> h; 435 const Heap::FibonacciHeap<int>::fibnode *x; 436 int a[]={3,7,1,2,3,12,5,4,-23,-4,0,2,-54},t=1; 437 int b[]={43,-23,12}; 438 int i,n=sizeof(a)/sizeof(int); 439 x=h.insert(a[0]); 440 for(i=1;i<n;++i) 441 h.insert(a[i]); 442 h.extract_min(); 443 h.Display(); 444 printf("-=-=-=-=-=-=-=-\n"); 445 h.kill(x); 446 h.Display(); 447 printf("-=-=-=-=-=-=-=-\n"); 448 printf("extract_min=%d\n",h.extract_min()); 449 return 0; 450 }






















 387
387

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








