【软件分析学习笔记】5：可达定义分析(Reaching Definitions Analysis)

最新推荐文章于 2023-10-24 23:07:01 发布

大桔骑士v

最新推荐文章于 2023-10-24 23:07:01 发布

阅读量5.4k

点赞数 15

分类专栏： # 软件分析文章标签：软件分析静态分析数据流分析控制流图可达定义分析

本文链接：https://blog.csdn.net/SHU15121856/article/details/105288593

版权

软件分析专栏收录该内容

5 篇文章

订阅专栏

本文深入探讨数据流分析的基本原理及其在程序优化与错误检测中的应用，重点讲解可达定义分析，包括其概念、算法设计及实例分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

从这节开始两节课先学习数据流分析的应用，再往后两节学习数据流分析的基本原理。这节学习可达定义分析，下节学习活跃变量分析和可用表达式分析，它们都是数据流分析的常见应用。

1 数据流分析回顾

数据流分析研究的是抽象出的application-specific data如何在控制流图(CFG)上流动，大多数静态分析都是在CFG上进行分析的。

1.1 safe-approximation

对大多数静态分析而言，都是牺牲complete来保证sound，要进行over-approximation，即may分析，这种时候分析出的错误中可能有误报，但是涵盖了要分析的所有错误。

还有一些静态分析是must分析，要进行under-approximation，要求报出的错误必须是真实存在的。例如，对于编译优化就需要进行must分析，如果使用may分析，那么对于那些误报的地方就会导致错误的优化。

无论是over的还是under的近似都是要保证分析的safety，都是为了迎合具体的使用场景下分析是安全的。所以可以统称safe-approximation，对于may分析safe=over，对于must分析safe=under。

1.2 不同的数据流分析

因为数据流分析是在CFG上，前面学习了，在CFG上结点(Node) 是基本块(BB)或者单条语句(statement)，用转换函数(transfer function) 得到新的抽象数据表示(data abstraction)。而对于边(Edge) 就是控制流(control flow)，也使用专门的处理方法(control flow handling)。

对于不同的数据流分析有不同的data abstraction，也有不同的safe-approximation策略，也有不同的transfer function和control flow handling。

2 预备知识

2.1 IR语句的输入输出状态

在得到中间表示(IR)的语句之后，用IN[s1]表示s1执行前的状态，用OUT[s1]表示s1执行后的状态，每个IN和OUT都关联一个语句执行前/后的程序点。
在这里插入图片描述
上图前两个很好理解，即流入方的IN就是流出方的OUT，第三个是控制流汇聚的情况，这个时候要对不同的场景设定不同的meet operator，用符号 $\wedge$ 表示，来汇聚多个流入的数据。

2.2 数据流分析要达到的效果

而数据流分析要达到的效果，就是给每一个程序点(program point) 关联一个数据流值(data-flow value) ，这个值代表在这一点能观测到的所有可能的程序状态(program state)的抽象。

注意，关联的data-flow value取值自值域(domain)，例如对于一段程序的符号分析：
在这里插入图片描述
从另一个角度理解，数据流分析是对那些IN和OUT所描述的一系列的safe-approximation约束规则进行求解，在CFG上约束规则就是这两类：

对statement的语义的约束规则，即基于transfer function
基于控制流信息的约束规则

下面分别简要说明。

2.3 基于transfer function的约束规则

有两种，前向分析(forward analysis) 和逆向分析(backward analysis)。

对于单条语句s，前向分析的transfer functionf_s就是将语句前程序点的状态IN[s]转换为语句执行后的OUT[s]；而逆向分析则是反过来，从OUT[s]得到IN[s]。
在这里插入图片描述
这里老师提到，有些时候说到backward analysis，实际做的时候是把整个CFG倒过来，然后再进行forward analysis完成的。正常时候就是理解成沿着CFG反着做就行了。

2.4 基于控制流信息的约束规则

多个statement组成BB，所以控制流信息就可以分为BB内部的和BB之间的。

对于BB内的statement，下一条的输入状态IN就是上一条的输出状态OUT。而整个BB的IN就是第一条语句的IN，整个BB的OUT就是最后一条语句的OUT。对于整个BB而言，其transfer function $f_B$ 就是里面每一条statement的transfer function结合在一起，从而可以从IN[B]计算OUT[B]。而要计算BB的IN[B]，就还是它的所有前驱BB进行meet运算( $\wedge$ )得到的。
在这里插入图片描述

3 可达定义分析(Reaching Definitions Analysis)

3.1 简述

先说明什么是"可达的定义"：在程序点 $p$ 的一个定义 $d$ ，到程序点 $q$ 是可达的，当且仅当这个定义在 $\to q$ 这条路径上不会被kill掉。

注意这里说的一个变量的定义(definition)即是指为这个变量设置值的statement，在程序语言中初始化和赋值都算是definition。

也就是说变量 $v$ 在 $p$ 处有definition，然后在 $\to q$ 不能被新的definition盖掉，这样它（指 $p$ 处 $v$ 的definition，而不是 $v$ 本身）在这条路径上就是可达定义(reaching definition)。

可达定义分析除了用于编译优化，也可以用作简单的错误检测。在上节学习的CFG中最开始有个额外的entry块，把程序中所有变量在这个entry块中添加一个dummy definition，用来指示这个变量还是未定义的状态。接下来在一个可达的程序点 $q$ 如果发现变量 $v$ 被使用了，并且 $v$ 的dummy definition在这里还是个可达定义，那么这里就可能发生了"使用未定义的变量"的错误（当然也可能没有，因为 $v$ 可以在其它path上有新的definition，程序运行时可能走了那条path），显然可达定义分析属于may分析。

3.2 definition的表示

可达定义分析用Bit Vector表示definition，如程序中有100个definition就用100个比特位来表示，从左往右第 $i$ 位就表示第 $i$ 个definition：
$D_1,D_2,...,D_{100} = 00...0$

3.3 transfer function的设计

对于程序中一个对变量 $v$ 的definition：
$\ op \ y$

它kill掉了前面所有的对 $v$ 的definition，因此基本块的transfer function的设计：
$GEN_{B} \ \cup \ (IN[B] - KILL_B)$

这里补一下郭老师的PPT：
在这里插入图片描述
这即是说：
$\begin{aligned} \text{B结束后的定义} &= \text{B中能到达结尾的定义} + \\ &\text{B开始前的定义} - \\ &\text{由于B中的重新定义而使得失效的那些定义} \end{aligned}$

这里特别注意 $K I L L [B]$ 的含义，实际上只要是 $B$ 中的定义的那些赋值，在 $B$ 之外的其它基本块中对这个变量的赋值全部都会被KILL掉。

例如，考虑下面这个CFG：
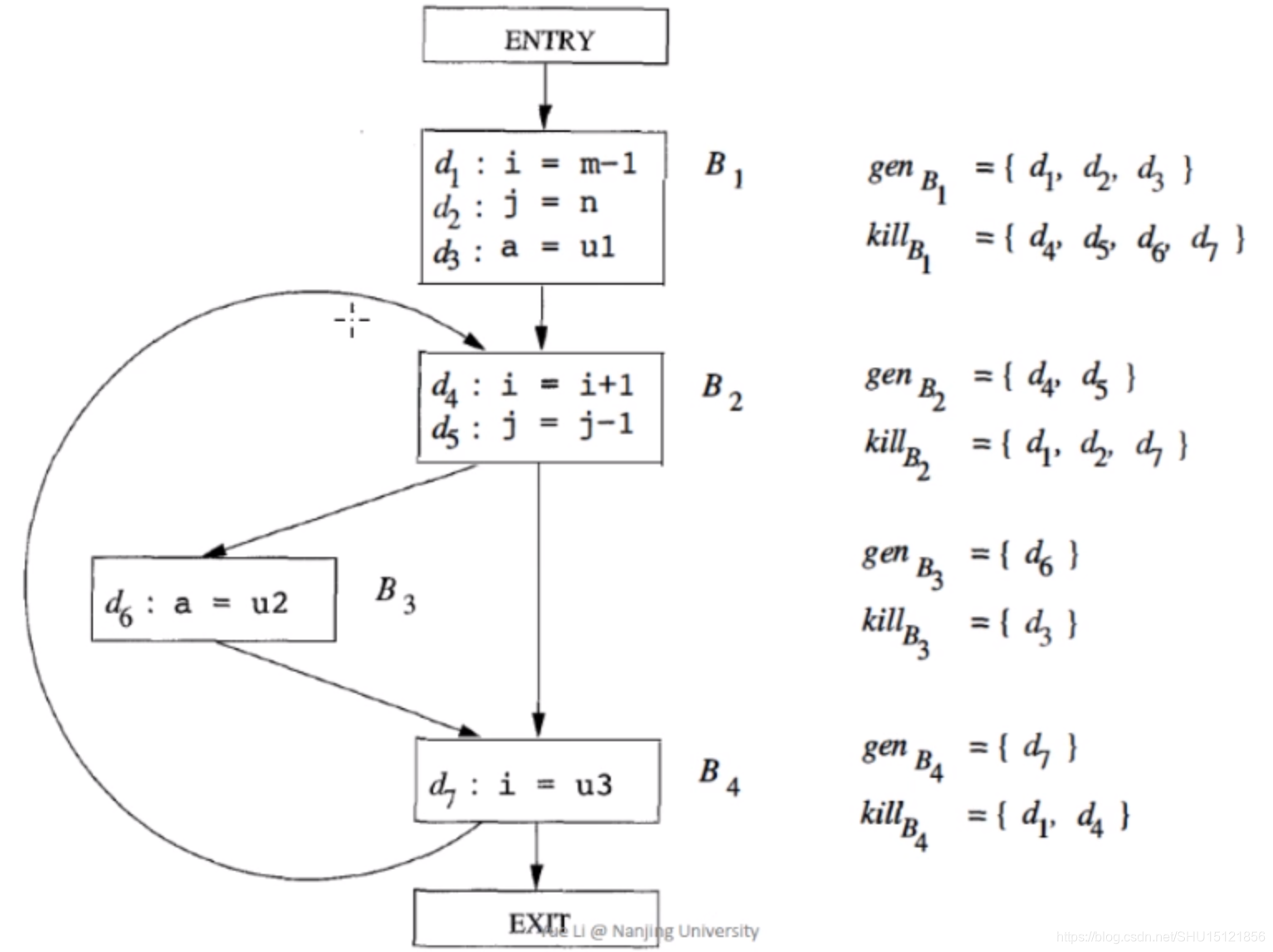
在这里插入图片描述
对于基本块 $B_1$ 而言，因为里面有对变量 $i$ 、 $j$ 、 $a$ 的定义，所以 $KILL_{B_1}$ 就是所有其它地方对这三个变量的定义。注意后面的 $d_4$ 和 $d_5$ 虽然不可能出现在基本块 $B_1$ 前面，但是还是要算进去，毕竟只是求一个差集，这样能保证那些循环回来的路径上的定义不会混入 $IN[B_1]$ 中而不被 $KILL_{B_1}$ 消除掉。

3.4 control flow的设计

回顾这节的2.4可以知道，实际上不同数据流分析的control flow的设计，区别就在于控制流合并时的meet操作( $\wedge$ )的不同。在可达定义分析中，这个操作是集合求并( $\cup$ )，即是说：
$\bigcup_{P是B的前驱} OUT[P]$

因为是may分析，一条path也不能放过，所以是所有前驱的OUT求并。

3.5 可达定义分析的算法

算法的输入是控制流图，输出就是对每个基本块 $B$ 都要得到 $I N [B]$ 和 $O U T [B]$ ：
在这里插入图片描述
第一步定义最上面的虚拟Entry块的OUT为空集，因为这个虚拟块中实际上没有definition，所以也就没有能流到OUT[Entry]这一程序点的definition，因此是空集。

第二步对所有除了Entry之外的基本块，将其OUT设置为空集。这里老师解释了一下，因为这个算法是一个数据流分析的比较经典的模板算法，对于有些数据流分析而言，Entry和其它基本块的boundary condition（这里指初始的边界条件）是不一样的，所以这里分开写了一下。实际上在这个算法里就是所有的基本块OUT先设置为空集。

数据流分析的boundary condition都可以靠思考语义去设计，比如在这里就要询问自己OUT[B]在这个分析中是什么含义，回答是从基本块流出来的程序状态，具体指有哪些definition可以到达这个程序点。
may分析的boundary condition一般都是空，must分析的boundary condition一般都是top。

接下来是一个while循环，一轮循环下来只要有一个BB的OUT改变了，这个循环就不会终止。在这个while循环内部有一个for循环遍历所有的除了Entry之外的BB，然后里面的两行就是为每一个BB不断执行3.3和3.4的约束规则。直到所有的OUT都不变了，结果就收敛了，程序就终止了。

3.6 可达定义分析的例子

在这里插入图片描述
一共有8个定义，用8位的Bit Vector表示：
$D_1D_2D_3D_4D_5D_6D_7D_8=00000000$

每个程序点都需要有这样一个Bit Vector，其中0表示在这点对应的definition不可达，1表示可达，所以空集其实就是这样8个0组成的Bit Vector。

先执行算法的第一第二步，将所有BB的OUT初始化为空：
在这里插入图片描述
接下来要不停应用循环体内的control flow策略求IN和transfer function求OUT：

在 $B_1$ 上执行data flow规则计算 $IN[B_1]$ ，由于前驱只有Entry块，所以 $IN[B_1]=OUT[Entry]=00000000$ 。

在 $B_1$ 上执行transfer function计算 $OUT[B_1]$ ，由于 $GEN_{B_1}$ 是 ${D_1,D_2\}$ ， $IN[B_1]$ 是空集， $KILL_{B_1}$ 是 ${D_4,D_5,D_7\}$ ，所以得到 $OUT[B_1]=11000000$ 。

在 $B_2$ 上执行data flow规则计算 $IN[B_2]$ ，由于前驱有 $B_1$ 和 $B_4$ ，其中 $OUT[B_4]=00000000$ ， $OUT[B_1]=11000000$ ，求并集（位运算的或）得 $IN[B_2]=11000000$ 。

在 $B_2$ 上执行transfer function计算 $OUT[B_2]$ ，由于 $GEN_{B_2}$ 是 ${D_3,D_4\}$ ， $IN[B_2]$ 是 ${D_1,D_2\}$ ， $KILL_{B_2}$ 是 ${D_2\}$ ，所以得到 $OUT[B_2]=10110000$ 。

在 $B_3$ 上执行data flow规则计算 $IN[B_3]$ ，由于前驱只有 $B_2$ ，所以 $IN[B_3]=OUT[B_2]=10110000$ 。

在 $B_3$ 上执行transfer function计算 $OUT[B_3]$ ，由于 $GEN_{B_3}$ 是 ${D_7\}$ ， $IN[B_3]$ 是 ${D_1,D_3,D_4\}$ ， $KILL_{B_3}$ 是 ${D_1,D_5\}$ ，所以得到 $OUT[B_3]=00110010$ 。

在 $B_4$ 上执行data flow规则计算 $IN[B_4]$ ，由于前驱只有 $B_2$ ，所以 $IN[B_4]=OUT[B_2]=10110000$ 。

在 $B_4$ 上执行transfer function计算 $OUT[B_4]$ ，由于 $GEN_{B_4}$ 是 ${D_5,D_6\}$ ， $IN[B_4]$ 是 ${D_1,D_3,D_4\}$ ， $KILL_{B_4}$ 是 ${D_1,D_7,D_8\}$ ，所以得到 $OUT[B_4]=00111100$ 。

在 $B_5$ 上执行data flow规则计算 $IN[B_5]$ ，由于前驱有 $B_4$ 和 $B_3$ ，其中 $OUT[B_4]=00111100$ ， $OUT[B_3]=00110010$ ，求并集（位运算的或）得 $IN[B_5]=00111110$ 。

在 $B_5$ 上执行transfer function计算 $OUT[B_5]$ ，由于 $GEN_{B_5}$ 是 ${D_8\}$ ， $IN[B_5]$ 是 ${D_3,D_4,D_5,D_6,D_7\}$ ， $KILL_{B_5}$ 是 ${D_6\}$ ，所以得到 $OUT[B_5]=00111011$ 。

第一轮遍历结束，这轮遍历中存在OUT发生变化的BB，因此还要继续下一轮遍历。

在 $B_1$ 上执行data flow规则计算 $IN[B_1]$ ，由于前驱只有Entry块，所以 $IN[B_1]=OUT[Entry]=00000000$ 。

在 $B_1$ 上执行transfer function计算 $OUT[B_1]$ ，由于 $GEN_{B_1}$ 是 ${D_1,D_2\}$ ， $IN[B_1]$ 是空集， $KILL_{B_1}$ 是 ${D_4,D_5,D_7\}$ ，所以得到 $OUT[B_1]=11000000$ 。

在 $B_2$ 上执行data flow规则计算 $IN[B_2]$ ，由于前驱有 $B_1$ 和 $B_4$ ，其中 $OUT[B_4]=00111100$ ， $OUT[B_1]=11000000$ ，求并集（位运算的或）得 $IN[B_2]=11111100$ 。

在 $B_2$ 上执行transfer function计算 $OUT[B_2]$ ，由于 $GEN_{B_2}$ 是 ${D_3,D_4\}$ ， $IN[B_2]$ 是 ${D_1,D_2,D_3,D_4,D_5,D_6\}$ ， $KILL_{B_2}$ 是 ${D_2\}$ ，所以得到 $OUT[B_2]=10111100$ 。

在 $B_3$ 上执行data flow规则计算 $IN[B_3]$ ，由于前驱只有 $B_2$ ，所以 $IN[B_3]=OUT[B_2]=10111100$ 。

在 $B_3$ 上执行transfer function计算 $OUT[B_3]$ ，由于 $GEN_{B_3}$ 是 ${D_7\}$ ， $IN[B_3]$ 是 ${D_1,D_3,D_4,D_5,D_6\}$ ， $KILL_{B_3}$ 是 ${D_1,D_5\}$ ，所以得到 $OUT[B_3]=00110110$ 。

在 $B_4$ 上执行data flow规则计算 $IN[B_4]$ ，由于前驱只有 $B_2$ ，所以 $IN[B_4]=OUT[B_2]=10111100$ 。

在 $B_4$ 上执行transfer function计算 $OUT[B_4]$ ，由于 $GEN_{B_4}$ 是 ${D_5,D_6\}$ ， $IN[B_4]$ 是 ${D_1,D_3,D_4,D_5,D_6\}$ ， $KILL_{B_4}$ 是 ${D_1,D_7,D_8\}$ ，所以得到 $OUT[B_4]=00111100$ 。

在 $B_5$ 上执行data flow规则计算 $IN[B_5]$ ，由于前驱有 $B_4$ 和 $B_3$ ，其中 $OUT[B_4]=00111100$ ， $OUT[B_3]=00110110$ ，求并集（位运算的或）得 $IN[B_5]=00111110$ 。

在 $B_5$ 上执行transfer function计算 $OUT[B_5]$ ，由于 $GEN_{B_5}$ 是 ${D_8\}$ ， $IN[B_5]$ 是 ${D_3,D_4,D_5,D_6,D_7\}$ ， $KILL_{B_5}$ 是 ${D_6\}$ ，所以得到 $OUT[B_5]=00111011$ 。

第二轮遍历结束，这轮遍历中存在OUT发生变化的BB（分别是 $B_2$ 和 $B_3$ ），因此还要继续下一轮遍历。

接下来的一轮遍历OUT全都不变，不再写出了，最终结果：
在这里插入图片描述

从整个流程跑下来可以发现， $KILL_B$ 和 $GEN_B$ 在每次循环中都是不变的，只和CFG本身有关，可以一开始就算好，每次拿来直接用就行了。

由此，只要输入 $I N [B]$ 和上一轮相比不变，那么输出 $O U T [B]$ 一定也不变。另外遍历的次序也很重要，上面用的是拓扑排序的遍历次序，这样只要花费较少的while循环次数。

3.7 为什么算法一定能终止

算法最关键的transfer function中GEN和KILL都是不变的，实际上只由IN的变化决定OUT的变化。而IN的变化即每次加入新的fact，只可能比之前多而不会比之前少，而新加入的部分可能在计算OUT的公式中被KILL掉，或者成为幸存者保留到OUT中，这导致OUT也只可能比之前多而不会比之前少。

总的来说，就是整个过程是不断加入fact，不断达到最终的sound的结果过程。反映到Bit Vector中即不可能存在某位=1变成该位=0的情况。
在这里插入图片描述