HDU3639 Hawk-and-Chicken

传送门
Problem Description
Kids in kindergarten enjoy playing a game called Hawk-and-Chicken. But there always exists a big problem: every kid in this game want to play the role of Hawk.
So the teacher came up with an idea: Vote. Every child have some nice handkerchiefs, and if he/she think someone is suitable for the role of Hawk, he/she gives a handkerchief to this kid, which means this kid who is given the handkerchief win the support. Note the support can be transmitted. Kids who get the most supports win in the vote and able to play the role of Hawk.(A note:if A can win support from B(A != B) A can win only one support from B in any case the number of the supports transmitted from B to A are many. And A can’t win the support from himself in any case.
If two or more kids own the same number of support from others, we treat all of them as winner.
Here’s a sample: 3 kids A, B and C, A gives a handkerchief to B, B gives a handkerchief to C, so C wins 2 supports and he is choosen to be the Hawk.
Input
There are several test cases. First is a integer T(T <= 50), means the number of test cases.
Each test case start with two integer n, m in a line (2 <= n <= 5000, 0 < m <= 30000). n means there are n children(numbered from 0 to n - 1). Each of the following m lines contains two integers A and B(A != B) denoting that the child numbered A give a handkerchief to B.
Output
For each test case, the output should first contain one line with “Case x:”, here x means the case number start from 1. Followed by one number which is the total supports the winner(s) get.
Then follow a line contain all the Hawks’ number. The numbers must be listed in increasing order and separated by single spaces.
Sample Input
2
4 3
3 2
2 0
2 1

3 3
1 0
2 1
0 2
Sample Output
Case 1: 2
0 1
Case 2: 2
0 1 2
Author
Dragon
Source
2010 ACM-ICPC Multi-University Training Contest（19）——Host by HDU

题目描述

有n个点，m条边，求出能到某一个点的其他点最多的点，以及能到这个（些）点的其他点的点数。

题解

直接做显然没法做，应该先tarjan缩点后再在DAG上进行计算。
一种好的方法是缩点后将原先的边倒过来进行计算，这样能避免一种不容易被考虑到的情况：

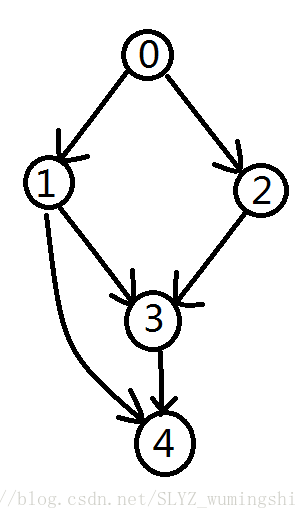
在这个图中，答案应该是4号点，这是显然的；但是在计算能到达4号点的点数时，如果直接算会导致算重，但如果反过来算就会避免这种情况。
ps：大家一定要在输出点的时候单独输出最后一个点，否则如果在最后出现多余的空格的话会导致PE！（也许可以尝试putchar一个退格键？反正我没试过）

CODE：

#include<cstdio>
#include<cstring>
const int N=5005;
const int M=3e4+10;
struct edge
{
    int nxt,to;
}a[M],e[M<<1];
int head[N],Head[N];
int dfn[N],low[N];
int block[N],size[N],in[N];
int s[N],top;
bool instack[N],isans[N];
int vis[N],Ans[N];
int tmp[N];
int T,n,m,x,y,num,Num,tot,Time,Tot,ans,ansnum;
inline int min(const int &a,const int &b){return a<b?a:b;}
inline void add(int x,int y)
{
    a[++num].nxt=head[x],a[num].to=y,head[x]=num;
}
inline void add2(int x,int y)
{
    e[++Num].nxt=Head[x],e[Num].to=y,Head[x]=Num;
}
void dfs(int now)
{
    dfn[now]=low[now]=++Time;
    instack[now]=1;
    s[++top]=now;
    for(int i=head[now];i;i=a[i].nxt)
      if(!dfn[a[i].to])
      {
        dfs(a[i].to);
        low[now]=min(low[now],low[a[i].to]);
      }
      else if(instack[a[i].to]) low[now]=min(low[now],dfn[a[i].to]);
    if(low[now]==dfn[now])
    {
        int tmp;
        tot++;
        do tmp=s[top--],instack[tmp]=0,block[tmp]=tot,size[tot]++;
        while(tmp!=now);
    }
}
int Dfs(int now,int root)
{
    int ans=size[now];
    for(int i=Head[now];i;i=e[i].nxt)
      if(vis[e[i].to]!=root) vis[e[i].to]=root,ans+=Dfs(e[i].to,root);
    return ans;
}
int main()
{
    scanf("%d",&T);
    for(int k=1;k<=T;k++)
    {
        memset(in,0,sizeof(in));
        memset(dfn,0,sizeof(dfn));
        memset(vis,0,sizeof(vis));
        memset(size,0,sizeof(size));
        memset(head,0,sizeof(head));
        memset(Head,0,sizeof(Head));
        memset(isans,0,sizeof(isans));
        num=Num=tot=Tot=Time=ans=ansnum=0;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
          scanf("%d%d",&x,&y),add(x+1,y+1);
        for(int i=1;i<=n;i++)
          if(!dfn[i]) dfs(i);
        for(int j=1;j<=n;j++)
          for(int i=head[j];i;i=a[i].nxt)
            if(block[j]!=block[a[i].to]) add2(block[a[i].to],block[j]),in[block[j]]++;
        for(int i=1;i<=n;i++)
          if(!in[i])
          {
            int tmp=Dfs(i,i);
            if(tmp>ans) Ans[Tot=1]=i,ans=tmp;
            else if(tmp==ans) Ans[++Tot]=i;
          }
        for(int i=1;i<=Tot;i++)
          isans[Ans[i]]=1;
        printf("Case %d: %d\n",k,ans-1);
        for(int i=1;i<=n;i++)
          if(isans[block[i]]) tmp[++ansnum]=i-1;
        for(int i=1;i<ansnum;i++)
          printf("%d ",tmp[i]);
        printf("%d\n",tmp[ansnum]);
    }
    return 0;
}