C++---状态压缩dp---愤怒的小鸟（每日一道算法2023.4.19）

注意事项：
难度警告！这题在NOIP中也算偏难的题，量力而行。
本题为"状态压缩dp—最短Hamilton路径"的扩展题，建议先阅读这篇文章并理解。
本题是"重复覆盖问题"可以使用"Dancing Links"做，但我们这里是用的状态压缩dp来写。

题目：
Kiana 最近沉迷于一款神奇的游戏无法自拔。   
简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 (0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟， 小鸟们的飞行轨迹均为形如 y=ax2+bx 的曲线，其中 a,b 是 Kiana 指定的参数，且必须满足 a<0。
当小鸟落回地面（即 x 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 n 只绿色的小猪，其中第 i 只小猪所在的坐标为 (xi,yi)。 
如果某只小鸟的飞行轨迹经过了 (xi, yi)，那么第 i 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行； 
如果一只小鸟的飞行轨迹没有经过 (xi, yi)，那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。

例如，若两只小猪分别位于 (1,3) 和 (3,3)，Kiana 可以选择发射一只飞行轨迹为 y=−x2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。 
这款神奇游戏的每个关卡对 Kiana 来说都很难，所以 Kiana 还输入了一些神秘的指令，使得自己能更轻松地完成这个这个游戏。   
这些指令将在输入格式中详述。

假设这款游戏一共有 T 个关卡，现在 Kiana 想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。  
由于她不会算，所以希望由你告诉她。

输入格式
第一行包含一个正整数 T，表示游戏的关卡总数。
下面依次输入这 T 个关卡的信息。
每个关卡第一行包含两个非负整数 n,m，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。
接下来的 n 行中，第 i 行包含两个正实数 (xi,yi)，表示第 i 只小猪坐标为 (xi,yi)，数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0，表示 Kiana 输入了一个没有任何作用的指令。
如果 m=1，则这个关卡将会满足：至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。

保证 1≤n≤18，0≤m≤2，0<xi,yi<10，输入中的实数均保留到小数点后两位。
上文中，符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整，例如 ：⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

输出格式
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入:
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00

输出：
1
1

#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;

typedef pair<double, double> PDD;
const int N = 20, M = 1 << 20;
int n, m, T;                        //T组数据，n为每组的小猪数量，m为询问的神秘指令类型(但其实没用到)
int path[N][N];                     //path[i][j]为 由点i和j生成的抛物线所组成的点集(除了i和j可能也同时包含其他点)，
int f[M];                           //f[i]为"当前点集覆盖状态为i的方案，属性为min(抛物线数量)"
PDD ver[N];                         //存储每个点的x和y值

int compare_float(double a, double b) {    //判断两个浮点数是否相同(c++的浮点数可能存在很小的误差)
    if (fabs(a - b) < 1e-8) return 0;
    if (a > b) return 1;
    return -1;
}

int main() {
    cin >> T;
    while (T -- ) {
        //读入每组数据
        cin >> n >> m;
        for (int i = 0; i<n; i++) cin >> ver[i].first >> ver[i].second;

        //预处理所有可能的抛物线，n个点，每两个点确认一条抛物线，所以是n^2条
        memset(path, 0, sizeof path);
        for (int i = 0; i<n; i++) {
            path[i][i] = 1 << i;            //穿过点i的直线必然会穿过点i
            for (int j = 0; j<n; j++) {
                double x1 = ver[i].first, y1 = ver[i].second;
                double x2 = ver[j].first, y2 = ver[j].second;
                if (compare_float(x1, x2) == 0) continue;  //单独一个点无法生成抛物线

                //计算y = ax^2 + bx中 a和b的值
                double a = (y1/x1 - y2/x2) / (x1 - x2);
                double b = (y1/x1) - (a*x1);
                if (compare_float(a, 0.0) >= 0) continue;   //抛物线的开口只能朝下，需要满足a<0

                //对于当前根据a和b生成的抛物线，求出该抛物线都穿过了哪些点，做成点集(二进制)
                for (int k = 0; k<n; k++) {
                    double x = ver[k].first, y = ver[k].second;
                    if (compare_float(y, a*x*x + b*x) == 0) path[i][j] += (1 << k);
                }
            }
        }

        //dp
        memset(f, 0x3f, sizeof f);
        f[0] = 0;   //初始化，点集状态为0时，抛物线数量为0，是合法方案
        for (int i = 0; (i+1) < (1 << n); i++) {   //枚举所有状态(如果全部为1就说明已经找到结果，不需要再做更新了)

            //找到任意一个没有被抛物线覆盖掉的点x(也就是在点集中为0)
            int x = 0;
            for (int j = 0; j<n; j++) {
                if ((i >> j & 1) == 0) {
                    x = j;
                    break;
                }
            }

            //枚举所有能覆盖掉点x的抛物线, 并更新状态
            for (int j = 0; j<n; j++) {
                int pre = (i | path[x][j]);
                f[pre] = min(f[pre], f[i] + 1);
            }
        }
        cout << f[(1<<n) - 1] << endl;      //全部为1的点集(每个小猪都被抛物线覆盖，且抛物线数量最少)即为答案
    }

    return 0;
}

思路：
基本思路就是先求出所有的可能的抛物线，再对每个抛物线进行状态更新。

一般抛物线方程：y = ax^2+bx+c，而题目中的抛物线有两个特点：
1.过原点(0,0), 即 c = 0
2.开口向下，即 a < 0
也就是说只要我们有两个点，就能计算出a和b的值，因此最多有 n^2个不同的抛物线：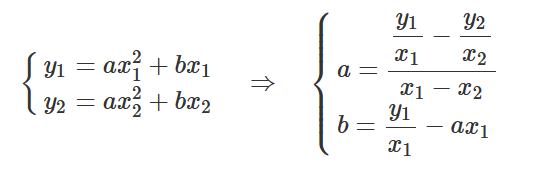

经典的y式dp法：
1.状态表示
f[i]: 当前点集覆盖为状态i的方案，属性为min(抛物线数量)。

(状态为 i 指的是二进制来表示当前抛物线覆盖小猪的状况，状压dp的常用手段，1表示被覆盖了，0表示未覆盖)

2.状态计算
状态转移：f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1)，

f[i] 表示能覆盖 i 状态的最小抛物线数量，而此时的 i 状态，还没覆盖 x 点。

path[x][j] 是由 点x和点j 组成的抛物线二进制点集，一定可以覆盖 点x，当然也可能包括其它点。

等于说在 f[i] 这些抛物线中再加入 path[x][j] 这条抛物线，则 点x 即被覆盖。

f[i | path[x][j]] 就是将新加入的这条 path[x][j] 抛物线所能覆盖的点和 f[i] 原有这些抛物线所能覆盖的点取并集，二进制下就是 “或” 运算。

如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力！

声明：
算法思路来源为y总，详细请见https://www.acwing.com/
本文仅用作学习记录和交流