Tea （思维）

Tea
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1058 Accepted Submission(s): 309

Problem Description
Tea is good.

Tea is life.

Tea is everything.

The balance of tea is a journey of pursuing balance of the universe.

Alice knows that.

Alice wants to teach you the art of pouring tea.

Alice has a pot of tea.

The exact volume of tea is not important.

The exact volume of tea is at least L.

The exact volume of tea is at most R.

Alice put two empty cups between you and her.

Alice wants the two cups filled by almost equal volume of tea.

Yours cannot be 1 unit more than hers.

Hers cannot be 1 unit more than yours.

Alice wants you to pour the tea.

Alice wants you to pour until the pot is almost empty.

Alice wants no more than 1 unit volume of tea remaining in the pot.

You cannot read the residue volume of tea remaining in the pot.

You can only know the tea status in the pot, empty or not.

Alice does not want you to pour the tea too many times.

You better pour as few times as possible.

Input
There are multiple cases.
For each case, there is one line of two integers L and R, separated by single space.

Here are some analyses about sample cases.
For the first case, pouring 1 unit into one cup will satisfy Alice.
For the second case, it is clearly that you cannot only pour once to reach the desired balance, but she can achieve it by pouring twice.
First you pour 1.5 units into one cup, then you attempt to pour another 1.5 units into the other cup.
Since the lower bound is 2, at least 0.5 unit remains in the pot after the first pouring.
If the initial volume is in range [2,3], the second cup will have volume in range [0.5,1.5] which is balanced with 1.5 unit in the first cup, and at most 1 unit remain after these two attempts.

About 1000 test cases, and 0≤L≤R≤1016.

Output
For each case, there should be a single integer in a single line, the least number of pouring attempts.

Sample Input
2 2
2 4

Sample Output
1
2

Source
2016 ACM/ICPC Asia Regional Qingdao Online

解题思路:
【题意】
有一壶水,你不知道里面具体的水量,只知道水量范围为[L,R]
现在要求你往两个无限大的杯子中倒水,使得两个杯子的水几乎一样多(即两个杯子中的水相差不超过1个单位)
且最终壶中水必须几乎倒空(即剩下的水量不超过1个单位)
你不知道壶中剩余多少的水,只知道壶倒空了没有
问至少需要几次倒水才能完成任务
【类型】
考察思维
【分析】
因为你不知道壶中有多少水,只知道范围为[L,R]
所以你倒的时候必须要先考虑到L
也就是说,第一次尝试倒水,我们最多只能倒L/2+0.5
因为就算壶中只有L的水,那剩下还有L/2-0.5的水可以倒进另一个杯子
这样子两个杯子相差1个单位的水量,是符合要求的
为了便于理解,我们可以抛开变量,使用常量
即假设L=11时,我们第一次尝试倒水可以倒L/2+0.5=5.5+0.5=6的水
那即便壶中只有11的水,那剩下还有5的水给另一个杯子,所以符合题意,这种情况最少倒2次就可以了
那么在最少倒两次的情况下,R最多能取到多少呢?显然,R=L+3=14

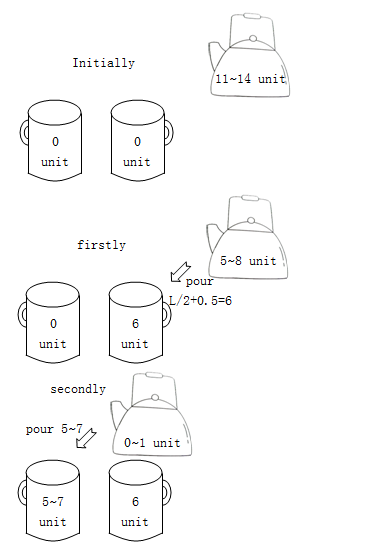
接下来,壶中水的上限R每增加2,就需要往水少的杯子中倒入2单位的水
最终可以得出结论
when R-L>=2,then the least number of pouring attempts is (R-L)/2+1
而R跟L相差1时,需要特判L=1,R=2这种情况,因为该情况下,只要往1个杯子中倒1个单位就可以了,这时另一个杯子没有水,而壶中最多剩1个单位的水
其他情况都至少需要2次
而R和L相等时,需要特判同为1和同为2的情况
同为1,显然不需要倒
同为2,往其中一个杯子中倒1个单位的水即可
其余情况至少需要2次
或许有人好奇,为什么一直没有提到L,R为0的情况
因为这种情况,我们知道壶是空的,所以不可能去倒,因此遇到为0时,就等同于1
【时间复杂度&&优化】
O(1)

AC代码：

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int main()
{
    __int64 L,R;
    while(~scanf("%I64d%I64d",&L,&R))
    {
        if(!L)
            L++;
        if(!R)
            R++;
        if(R-L>=2)
            printf("%I64d\n",(R-L)/2+1);
        else if(L==R)
        {
            if(L==1)
                puts("0");
            else if(L==2)
                puts("1");
            else
                puts("2");
        }
        else
        {
            if(L==1&&R==2)
                puts("1");
            else
                puts("2");
        }
    }
    return 0;
}