参考链接:简要理解DFT_我叫夏满满的博客-CSDN博客_dft原理
FFT(快速傅里叶变换)其本质就是DFT,只不过可以快速的计算出DFT结果。要理解FFT,必须先理解DFT(DiscreteFourier Transform) 。下面详细讨论DFT,因为DFT懂了之后,FFT就容易的多了。
DFT(FFT)作用:可以将信号从时域变换到频域,而且时域和频域都是离散的,通俗的说,可以求出一个信号由哪些正弦波叠加而成,求出的结果就是这些正弦波的幅度和相位。
首先我们要理解为什么一个周期非正弦信号可以拆分出某些频率的正弦波,从下图中可以直观的帮助我们理解。
Q:为什么可以求出正弦波的幅度?
这里就要说一下信号的相关性了,我们可以利用信号的相关性检测信号波中是否含有某个频率的信号波:把一个待检测信号波乘以另一个信号波,得到一个新的信号波,再把这个新的信号波所有的点进行累加,从相加的结果就可以判断出这两个信号的相似程度,比如下图:
上图中a,b是待检测信号,c,d是3个周期的正弦信号。很显然a图中含有正弦波:
然后将e图的各点相加,很显然值是正的,这就说明a图中含有与b图同频率的正弦波。
下面我们来看第二个例子:
显然将f图中各点相加结果约等于0了,这说明b图中不含有与b图同频率的正弦波。
这就是DFT的原理,其实就是这么简单,只不过DFT将待检测信号和很多不同频率的正弦波和余弦波相乘,也就是进行了信号相关性检测,从而可以计算出信号中含有的正弦波的幅度,若含有此频率的正弦波,那么幅值不为0,若不含有此正弦波,那么幅值为0。
下面来看一个具体的例子来理解:
图一即为待检测信号,也就是将进行DFT变换的信号,将它分成16个离散的点。图2是一个频率为1的正弦波,也分成16个点。将对应的点相乘,得到图3,再将图3的各个点的幅值相加,结果为10.06。也就是说图1中的图像含有图2的正弦波,此时用到的DFT点数就为16。那么幅度计算公式如下:
即含有的频率为1的正弦波的幅度就是1.25。以此类推,若要求是否含有频率为2的正弦波,将图1和频率为2的正弦波相乘再求和。
Q:为什么要除以呢?
图片来源于: 关于FFT频谱幅度要乘2/N的理解 - 哔哩哔哩
下面我们再开始理解DFT:
DFT的计算公式如下:
其中X(k)表示DFT变换后的数据;x(n)为采样后的模拟信号;N为做DFT的点数;n为序列的长度;公式中的x(n)可以为复信号,实际当中x(n)都是实信号,即虚部为0。此时上式根据欧拉公式可以展开为:
从这个公式可以看出,变换后的数据就是原信号对cos和sin的相关操作,即进行相乘求和(同上述计算信号相关度)。
附:欧拉公式

Q:为什么要将n\N写在2kpi后面呢?
因为在对cos和sin进行相关操作时,k代表和频率为多少的正弦相关。而n和N则是在一个正弦周期内采样N个点,采样间隔为2pi\N,n用来步进,一次步进2pi\N,最后进行累加求和,就得出了X(k)。另外,DFT之后的数据是对称的,比如做8点DFT,采样信号为x(n),DFT之后的数据为X(k),那么X(0)为直流信号,X(1), X(2), X(3), X(5), X(6), X(7),关于X(4)对称,即X(1)=X(7), X(2)=X(6),X(3)=X(5)。
下面我们在代码中实现一次简单的DFT:
from numpy import arange, sin, pi, cos
import matplotlib.pyplot as plt
import cmath
from scipy.fftpack import fft,ifft
Kl = arange(0, 256, 1)
Xk = [] # 创建保存DFT结果的数组
f0 = 1 # 原始信号频率
fs = 16 # 采样频率
N = len(Kl) # 原始信号点数
y = [1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0] # x[n]
for k in Kl: # 求 X[k] k = 1....N
temp = 0
for l in range(0, N): # 求X[k]
cm = 1j
cm *= -2*pi*l*k/N
temp += y[l]*cmath.exp(cm)
temp = temp
Xk.append(abs(temp))
yy = fft(y)
yf = abs(yy) # 用python自带的FFT验证
plt.plot(Kl, Xk, label="DFT")
plt.plot(Kl, yf, label="python FFT")
plt.plot(Kl, y, label="square wave")
plt.legend(loc="lower right")
plt.show()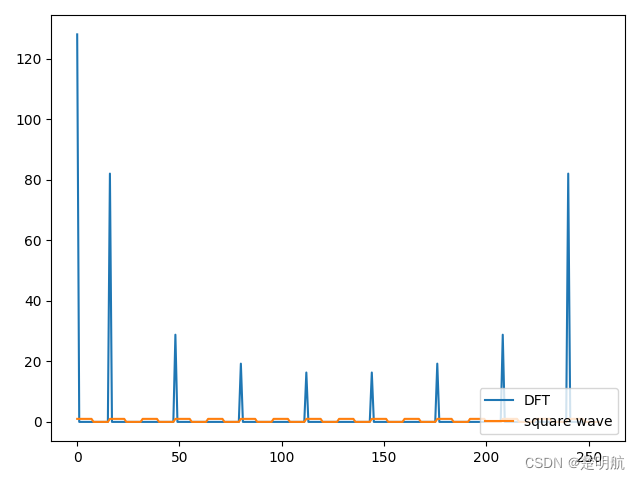








 本文深入探讨了离散傅里叶变换(DFT)及其快速算法FFT,阐述了DFT如何将时域信号转换到频域,并通过实例解释了正弦波幅度的计算方法。DFT通过计算信号与不同频率正弦波的相关性来确定信号成分,而FFT则提高了计算效率。文中还通过代码展示了DFT的实现过程,帮助读者更好地理解DFT和FFT的基本原理。
本文深入探讨了离散傅里叶变换(DFT)及其快速算法FFT,阐述了DFT如何将时域信号转换到频域,并通过实例解释了正弦波幅度的计算方法。DFT通过计算信号与不同频率正弦波的相关性来确定信号成分,而FFT则提高了计算效率。文中还通过代码展示了DFT的实现过程,帮助读者更好地理解DFT和FFT的基本原理。






















 821
821

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








