目录
一、定义:
✨基数是指一个数制系统中所使用的数码的数目。在大多数常见的数制中,基数是2(二进制)、8(八进制)、10(十进制)和16(十六进制)✨
👉例如:在十进制系统中,基数是10,意味着我们使用0到9这10个数字来表示所有的数值(也是我们生活中经常会用到的)。在二进制系统中,基数是2,只使用0和1。基数的选择影响了数值的表示方式和计算规则。
✨ 不过,在我们使用的电子计算机中所有数据都是ON/OFF信号(即1和0)来表示的,对我们来说容易理解的是十进制,🐸对于计算机来说容易理解的是以2为基数的二进制更容易理解。
二、各个进制:
1、二进制:
✨ 用 0 1 表示,当2种数字用完,就要进位👉下图,我用的二进制的相加,中间的式子和我们十进制的数相加类似,当满足2是就向前进一位,也就是所每位最高只能是1
2、八进制:
✨用 0 1 2 3 4 5 6 7 表示,当这些数字用完了,就要进位👉下图,用八进制表示,相加,大于等于8就要向前进一位
3、十进制:
✨用0 1 2 3 4 5 6 7 8 9 表示,当这些数字用完了,就要进位👉下图,我们平常接触最多的,一看也明白吧!10进1
4、十六进制:
用 0 1 2 3 4 5 6 7 8 9 A B C D E F 表示 ,A-F用小写也一样,没区别,当这些数字用完了就要进位👉当该位上的值大于等于16就要向前进1
其实无论是以那个基数作为进制,底层的值都是一样的
三、基数转换:
✨不同的基数底层是一样的原理,所以我们可以通过转换,将不同基数间的值转换为同基数
1、各类基数转十进制:
✨一句话:按权展开
在十进制中,以1998为例子:👉🐸 各个位乘以相对应的位数
这个思路同样能用到其他基数: 这样就能轻轻松松的将这些数字转换为十进制数
二转十:
以101为例子,按权展开
八转十:
以123为例子,按权展开
十六转十:
以1FD为例子,按权展开
2、十进制转各类基数;
✨✨口诀:除以相对应的基数,取余数,倒叙排列✨✨
先看一个例子:十进制的数转十进制

记住上面的口诀就可以了
总之就是这样:
✨10转2就是除2,取余倒序
✨10转8就是除8,取余倒序
✨10转16就是除16,取余倒序
3、二进制转八、十六进制的相互转换:
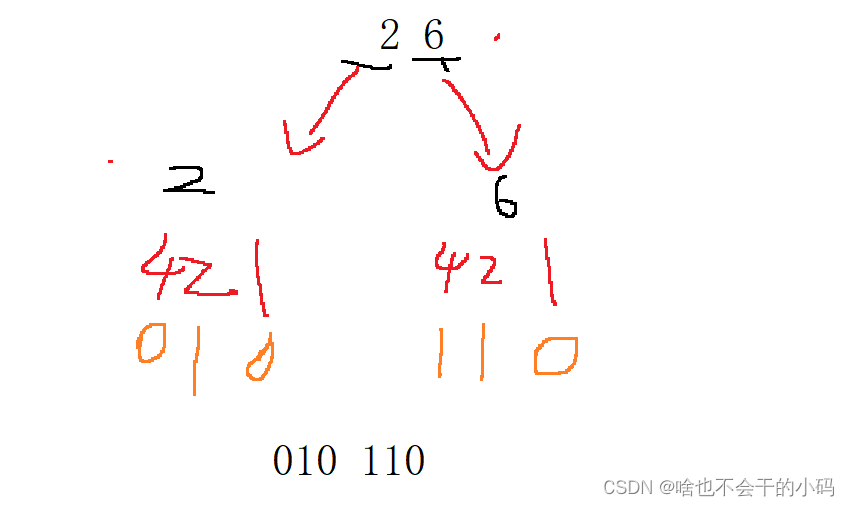
二转八: 421法
✨我们将二进制数从右边第一个数,往左走,每3位看成一个组 从左往右为第一组,第二组以此类推 ;通过“421”法进行转换为八进制的第一位、第二位、第三位等等
补充一句:不足3位的前面补0

👉👉看例子就能理解了;101 111的八进制就是57

八转二:421法逆推
对八进制的每一位分开 对每一位 进行除2取余数 转为 二进制

👉👉👉 还有一种逆推421法 就是取出每位,然后看那一位上的数是421 上那几个位组成
二转十六:8421法
✨和421法类似,这里是从左边往右边开始,取4位为一组,“8421”法十六进制 不足4位的前补0

十六转二:8421的逆推
可以对十六进制每一位除以2取余数 不够位数前面得补0

👉 逆推和八转二类似
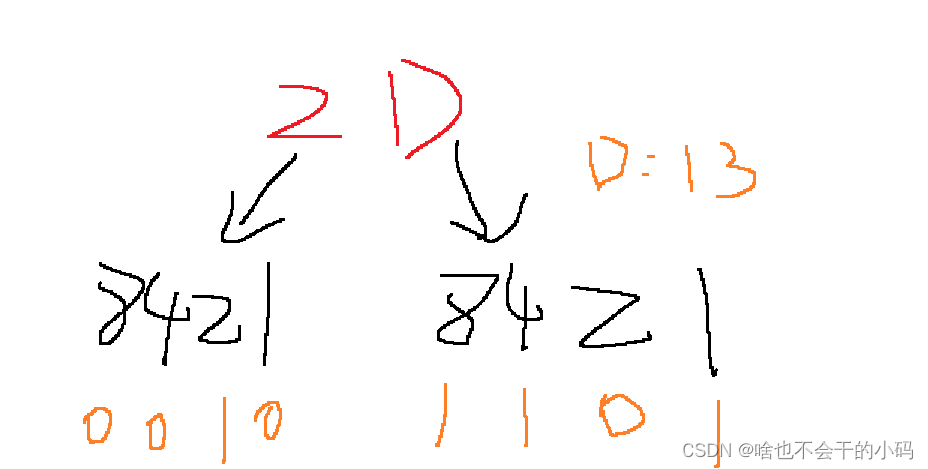
4、小数部分二转各个基数:
二转十:
非小数部分,按权展开,小数部分为2得-1 -2 -3……

二转八:
以小数点为分界线,继续使用 421法

二转十六:
以小数点为分界线,继续使用 8421法

四、总结:
二转八:“421法”
二转十六:“8421法”
任何基数转十进制:按权展开
十进制转任何基数:除以对应基数,取余倒叙排列
八进制、十六进制转二进制:每一位除以2,取余倒叙排列
希望本章节内容可以让你对于进制转换更加理解










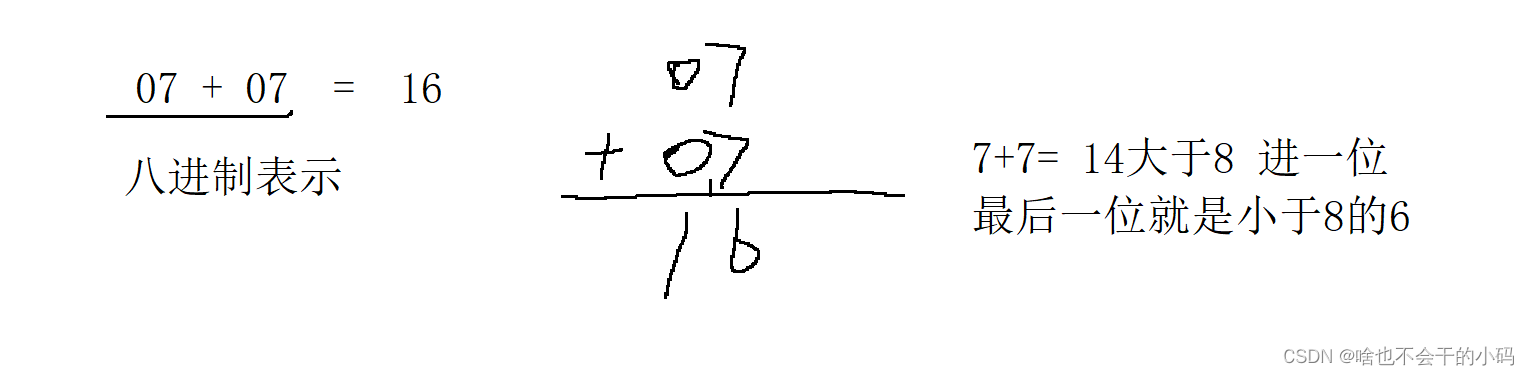



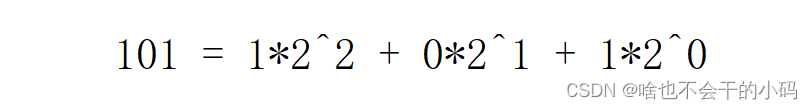


















 1179
1179

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








