ROC图以及AUC的实现代码

最新推荐文章于 2023-03-15 21:21:54 发布

Sasuke546

最新推荐文章于 2023-03-15 21:21:54 发布

阅读量2.2k

点赞数

这篇文章的内容均翻译自这篇文章：

ROC Graphs: Notes and Practical Considerations for Researchers
Tom Fawcett (tom.fawcett@hp.com)

给出一个二元分类器和实例，那么就有4种分类结果，True Positive, False Positive, False Negative,

True Negative，表示真实结果与分类结果的关系。然后，我们就分别有下列的式子，

ROC图是一种二维图，横轴是FP，纵轴是TP，这种图描述了一种获利（benefit）与花费（cost）的平衡关系。离散分类器

是只输出一个分类标记的分类器，每个离散分类器产生一个（FP，TP）点反映在ROC图中。

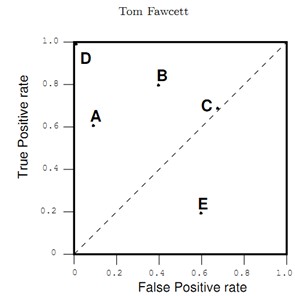
ROC图中的两个点需要特别注意，首先是（0，0），他表示分类器完全不输出正类样本中，虽然他不产生FP的错误，但也没有TP。

（1，1）则相反。（0，1）表示完美的分类结果。因此，出现在左上点的分类器更具有说服力，因为他们更准确而产生较少错误。

对角线y=x表示一种随机猜测的策略。

一些分类器对每个实例输出一个概率的结果，一个数值表示该样本更属于哪种类别，这种分类器需要一个域值来确定其结

果（正负类），即如果结果超过域值，将其定为Y，否则为N，每一种域值将产生一个ROC点。假设我们的域值的范围从负无穷到正

无穷，因此就能产生一个ROC的曲线。

AUC

ROC曲线是分类器在二维上的性能描述，但我们仍希望用一种标量值来表达分类器的性能，一种通用的方法就是计算ROC曲线下的

面积(Area Under the Curve)。因为AUC是单位正方形中的一部分，因为其面积总是在0到1之间。由于随机猜测的分类结果产生了一条

对角线，面积是0.5，因此正常的分类器其面积应当不小于它。

AUC有一个重要的统计特性，一个分类器的AUC等于分类器把随机选择的正实例排名高于随机选择的负实例的概率

（The AUC has an important statistical property: the AUC of a classier is equivalent to the probability that the classier will rank a

randomly chosen positive instance higher than a randomly chosen negative instance.）

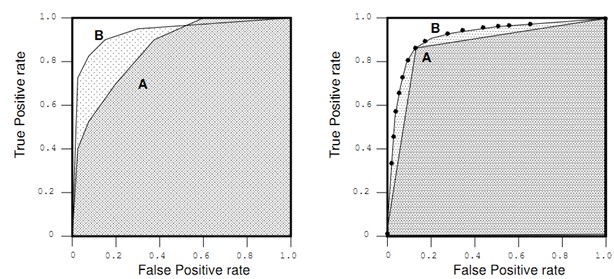
两个ROC图，左图显示了两个ROC曲线下的面积，右图显示了A（离散分类器）和B（概率分类器）

曲线下的面积

如图所示，B分类器的AUC较大，因此它的平均性能要忧于A。右图中展示了二元分类器A和数值（score）分类器B，当A与B

在固定点时，他们的性能是相同的，但是后面A就越来越逊于B了。

AUC的计算方法实际上是计算每个离散ROC点之间所形成的梯形面积来估算的。

以下是Matlab的代码

输入score是分类器的输出向量，label是实际的标签，P是正类的样本数，N是负类的样本数，在标签中，正类是2类，负类是1类

function [ Area ] = AUC( score , label, P, N )

    function [ A ] = Trapezoid_area(x1,x2,y1,y2)   % Area of Trapezoid

        base = abs(x1-x2);
        height = (y1+y2)/2;

        A =  base*height;

    end

    function [ f ] = equal(a,b)    % isequal

        if(abs(a-b)<1e-8)
            f = 1;
        else
            f = 0;
        end

    end
%AUC Summary of this function goes here
%   Detailed explanation goes here

[Y,ind]=sort(score,'descend');  % sort, Y is the vector after sort
                                % ind is the index of the original place

NS = size(score,2);

FP = 0;
TP = 0;

FPpv = 0; TPpv = 0;

Area = 0; fprev = -999999999;

i = 1;

while (i<=NS)
    
    if(equal(Y(i),fprev)==0)  % not equal
        Area = Area + Trapezoid_area(FP,FPpv,TP,TPpv);
        fprev = Y(i);
        FPpv = FP;
        TPpv = TP;
    end
    if(label(ind(i))==2)   % instanse i is positive
        TP = TP +1;
    else                   % negative
        FP = FP + 1;
    end
    
    i = i + 1;
    
end

Area = Area + Trapezoid_area(N,FPpv,P,TPpv);
Area = Area/(P*N);


end