遗传算法玩十步万度

ScienceLimit

已于 2024-04-19 18:16:16 修改

阅读量1.9k

点赞数 5

分类专栏：遗传算法十步万度文章标签： python 游戏算法

于 2021-05-04 20:15:05 首次发布

本文链接：https://blog.csdn.net/ScienceLimit/article/details/116108469

版权

遗传算法同时被 2 个专栏收录

2 篇文章 1 订阅

订阅专栏

十步万度

1 篇文章 0 订阅

订阅专栏

故事起因：
闲逛TapTap时看到了一个游戏十步万度，看到论坛里有人用代码过关，就自己玩了一下。
刚好最近学校学了遗传算法，突然想到可以用遗传算法求解，
梦幻联动

一、游戏代码实现

玩法

规则： 每点击一个指针它会顺时针旋转90度，之后该指针所指方向的指针也会顺时针旋转90度。（连锁效应，类似多米诺骨牌二维化）
目标： 在限定点击次数下使指针旋转度数总和最多。
例：第一关中点击左上角的指针2次，便达到了450度。
在这里插入图片描述
可以玩玩别人写的网页版（10000度那关）

代码实现

对指针编码：
如图：把四个指针依次编码为0123（为方便，后面均以该图为例）
在这里插入图片描述
其他关卡的地图指针编码顺序都是从0开始，从左到右，从上到下。
如：

玩家操作编码：
数组有序存储十个数表示玩家按该顺序点击十次。
数组里存储的值表示指针编码，取值范围取决于指针的数量。
例： [0 0 0 0 0 3 3 3 3 3] ：点击标号为0的指针5次，再点击标号为3的指针5次

在这里插入图片描述

方向编码：
0，1，2，3 表示上，右，下，左四个方向。（游戏里指针初始方向为上，顺时针90度后依次为右，下，左）。
因为每次指针都是顺时针旋转90度，所以转动后的方向 = （原方向 + 1 ） % 4
存储指针及其位置：
例如第一关
在这里插入图片描述
在代码中用两个数组存储，map1000为第一关中指针初始方向及分布状态，index1000为第一关中各指针的位置。
map1000存游戏第一关中指针初始方向及分布状态:
-1表示出界，其余数字表示该位置指针的方向编码，一般指针初状态都指向上，也就是0。
编码为n的指针在map1000中的位置用index1000存储：
行：index1000[n][0]，列：index1000[n][1]

map1000 = [[-1, -1, -1, -1],
           [-1,  0,  0, -1],
           [-1,  0,  0, -1],
           [-1, -1, -1, -1]]

index1000 = [[1, 1], [1, 2],
             [2, 1], [2, 2]]

例如3500的关卡：
在这里插入图片描述

map3500 = [[-1, -1, -1, -1, -1],
           [-1, -1,  0,  0, -1],
           [-1,  0,  0,  0, -1],
           [-1,  0,  0,  0, -1],
           [-1,  0,  0, -1, -1],
           [-1, -1, -1, -1, -1]]
index3500 = [        [1, 2], [1, 3],
             [2, 1], [2, 2], [2, 3],
             [3, 1], [3, 2], [3, 3],
             [4, 1], [4, 2]         ]

要修改的话只要把不是指针的位置改为-1，在index里删掉该位置的信息就行了。
这样每一关都要修改map和index，为方便，把所有关卡的信息都写到Map.py文件里，需要的时候直接引用。
主要功能函数函数
传入：地图map，指针位置index，玩家操作数组operands
返回：分数
运行时只需改变传入的参数map和index即可更换关卡。
省去了游戏页面显示等功能，代码相对较少。

def star(map, index, operands):   # 输入地图map，表的位置index，玩家操作operands，返回分数
    thisMap = [l[:] for l in map] # 不能修改 Map 里的原地图，所以先复制
    score = 0
    for operand in operands:  # 依次读取玩家点击的指针标号

        # r,c表示下一个转动的指针在第r行c列
        r = index[int(operand)][0]
        c = index[int(operand)][1]
        
        while( thisMap[r][c] != -1 ): # 当下一个转动的指针不在界外时，产生蝴蝶效应
            # 改变指针方向，分数增加90
            thisMap[r][c] = (thisMap[r][c] + 1) % 4
            score += 90

            # 顺着该指针所指方向改变r，c，得到下一个转动的指针位置
            if(thisMap[r][c] == 0):   # 指向上
                r -= 1
            elif(thisMap[r][c] == 1): # 指向右
                c += 1
            elif(thisMap[r][c] == 2): # 指向下
                r += 1
            else:                     # 指向左
                c -= 1

    return score

其他通关方式

大力出奇迹

随机： 随机生成许多个操作数组，再选出得分最高的数组。
遍历： 得出关卡里所有可能的操作数组，选出得分最高的。
但这两种方式能不能通关就看奇迹了，假设关卡里有pNum个指针，玩家可以点击clickNum次，则共有pNum的clickNum次方种情况，最简单的第一关就有4^10种。

二、遗传为主，贪心为辅

十步万度：找高维点集最值

玩家点击十次就要用十个整数变量表示玩家点击次序，指针数量决定变量取值范围。
例如第一关中前两步点击相当于有两个变量，这两个变量在游戏中对应得分的点集：

得分（z轴）	450	360	360	270	360	270	270	180	360	270	270	270	270	180	270	180
点击次序（x,y轴）	[0,0]	[0,1]	[0,2]	[0,3]	[1,0]	[1,1]	[1,2]	[1,3]	[2,0]	[2,1]	[2,2]	[2,3]	[3,0]	[3,1]	[3,2]	[3,3]

把这些点在三维空间中画出来：
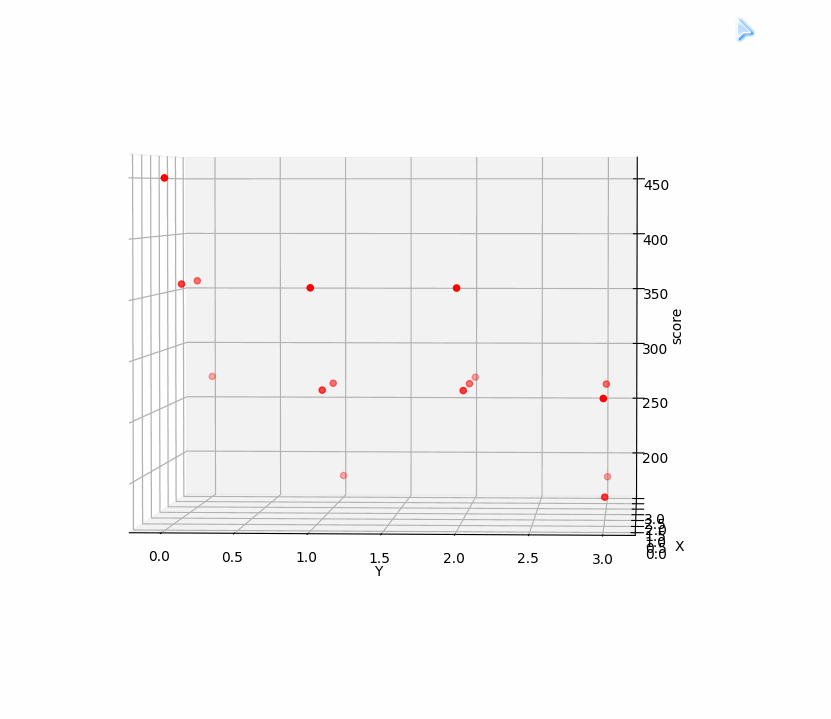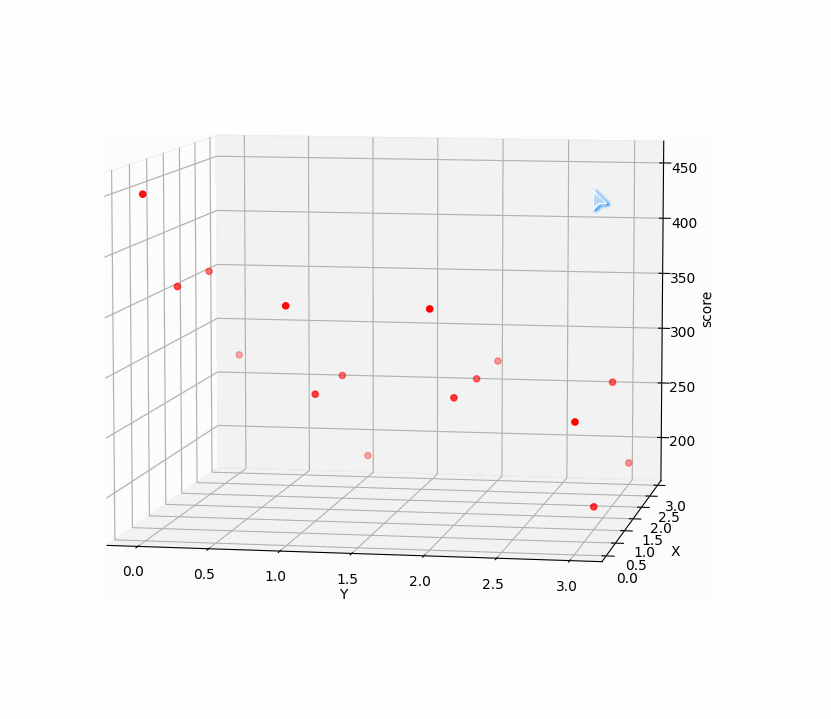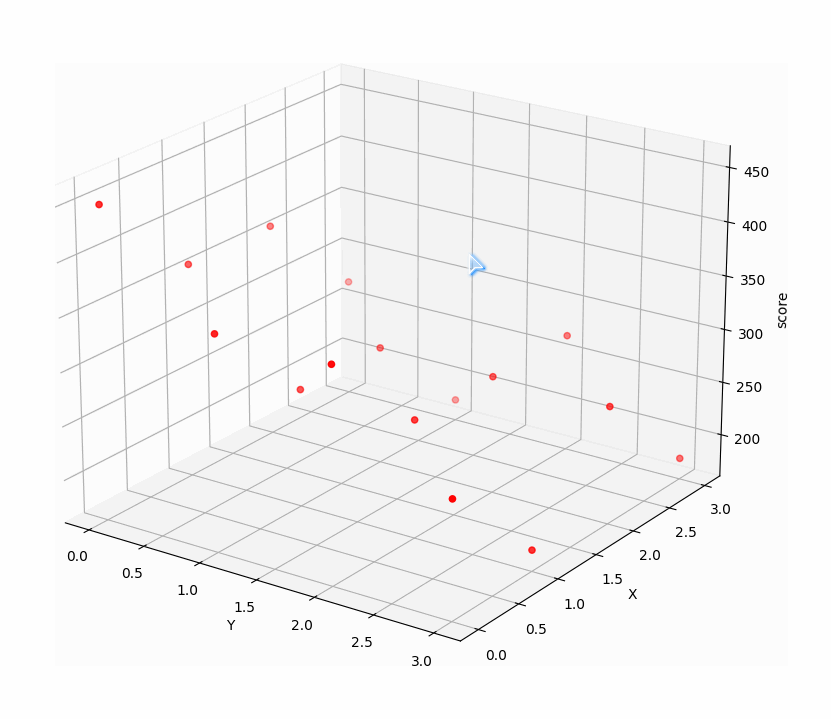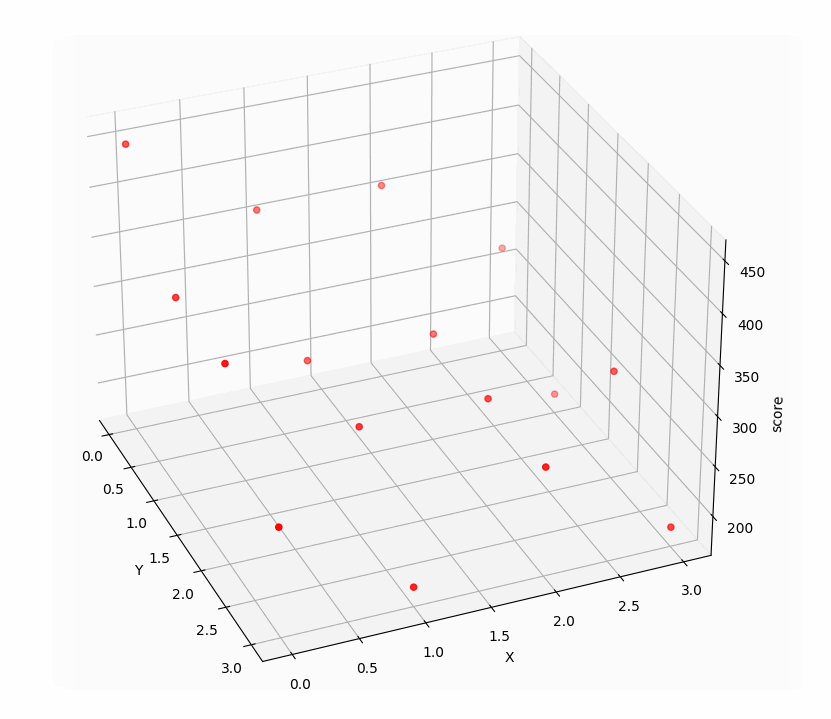
在这里插入图片描述
显然 [ 0, 0 ] 得到的分数450是这些点集中的最大值，也就是三维图中的最高点 [ 0, 0, 450 ] ，而游戏中 [ 0, 0 ] 正表示连续点两下0号表，也就是前两步的最优解。

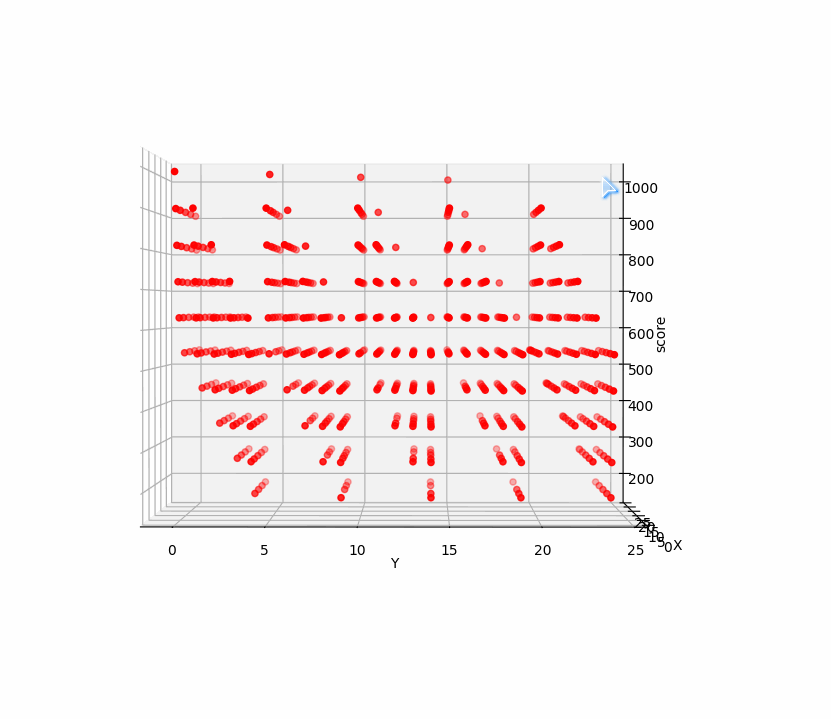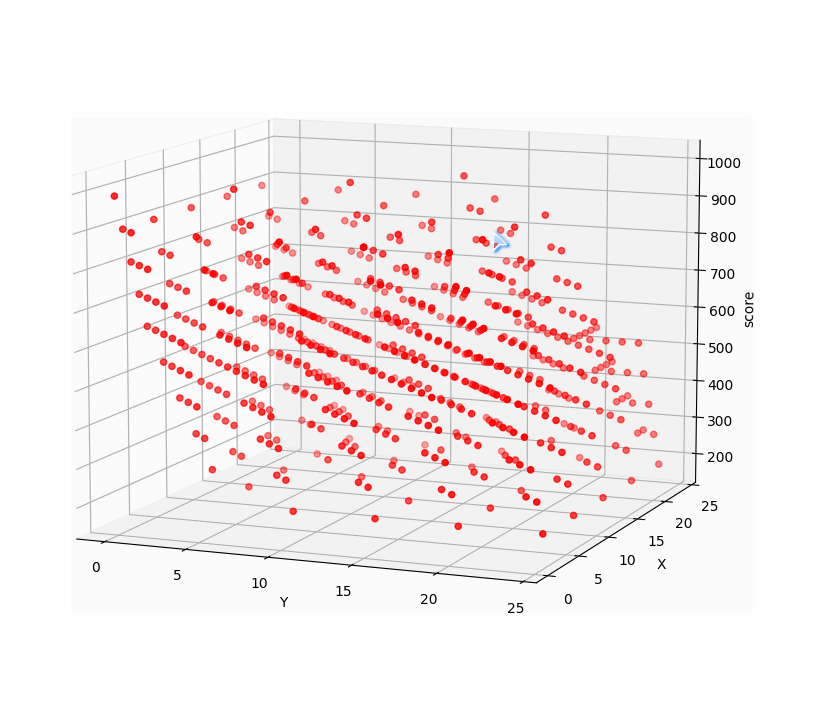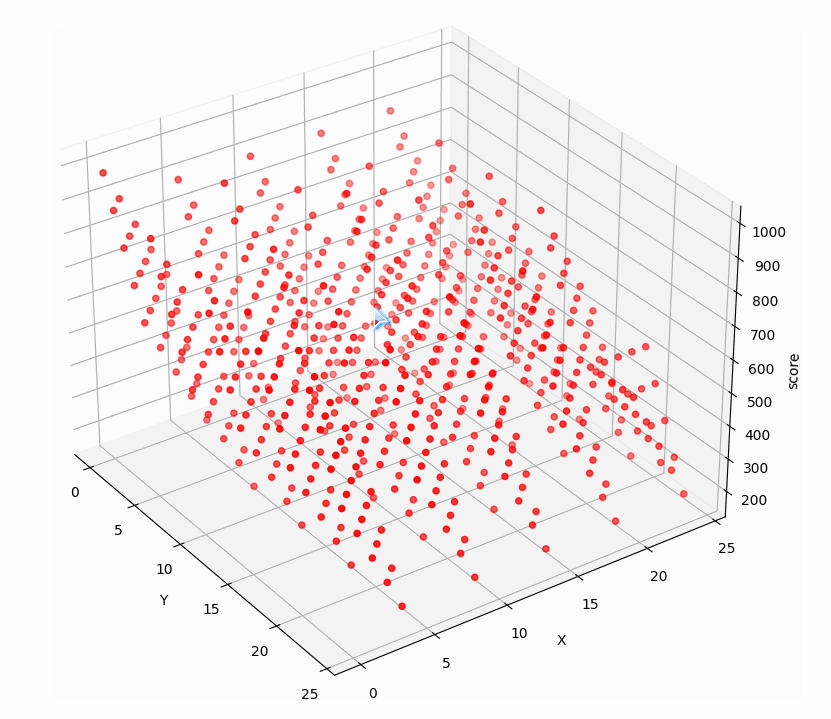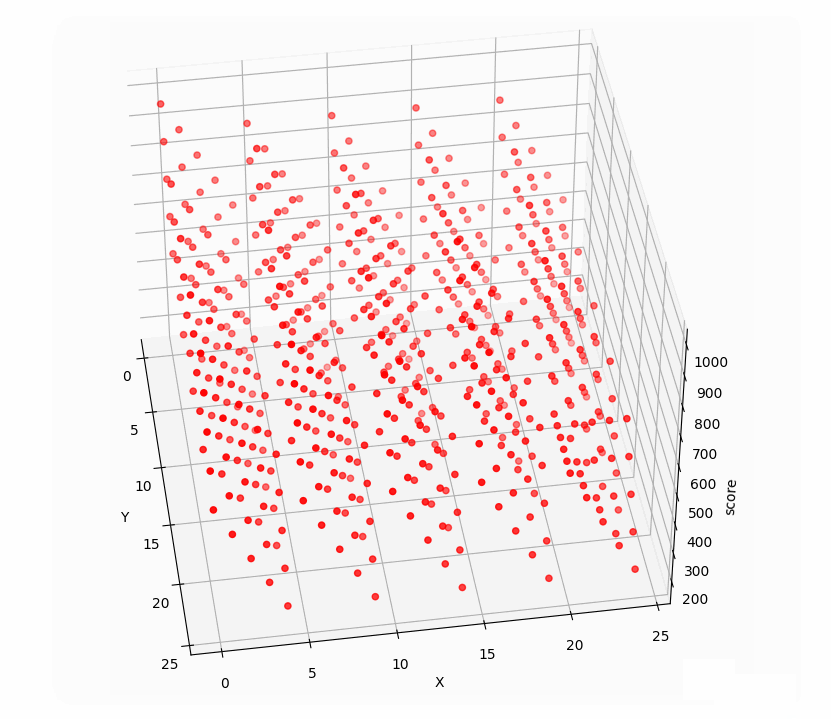
再看看10000的关卡前两步三维点集：

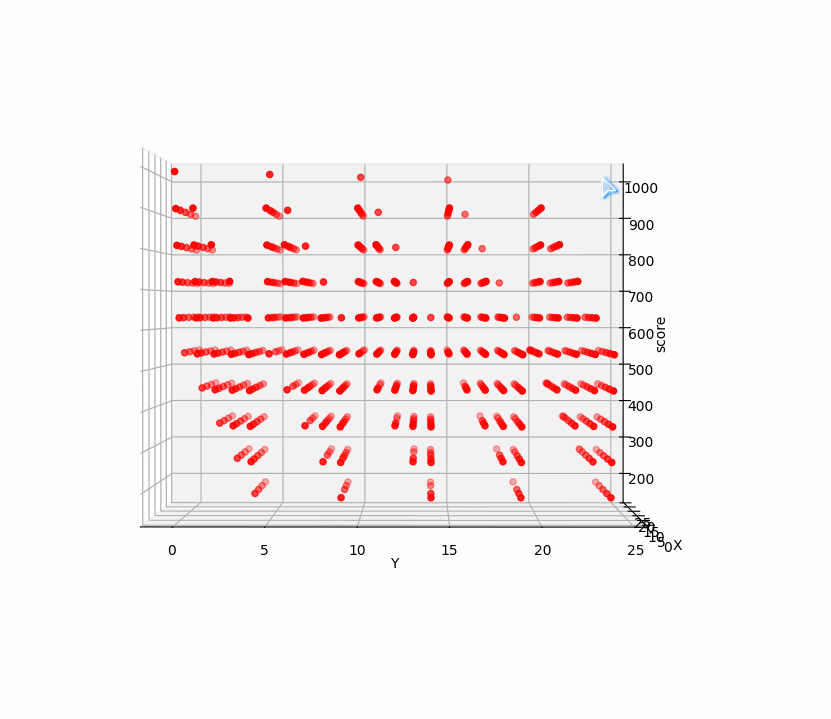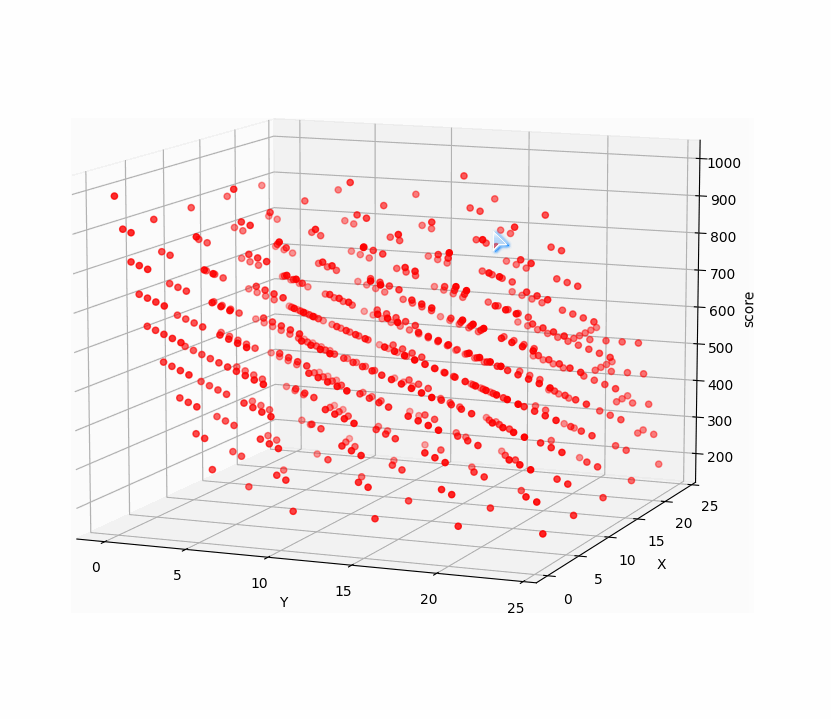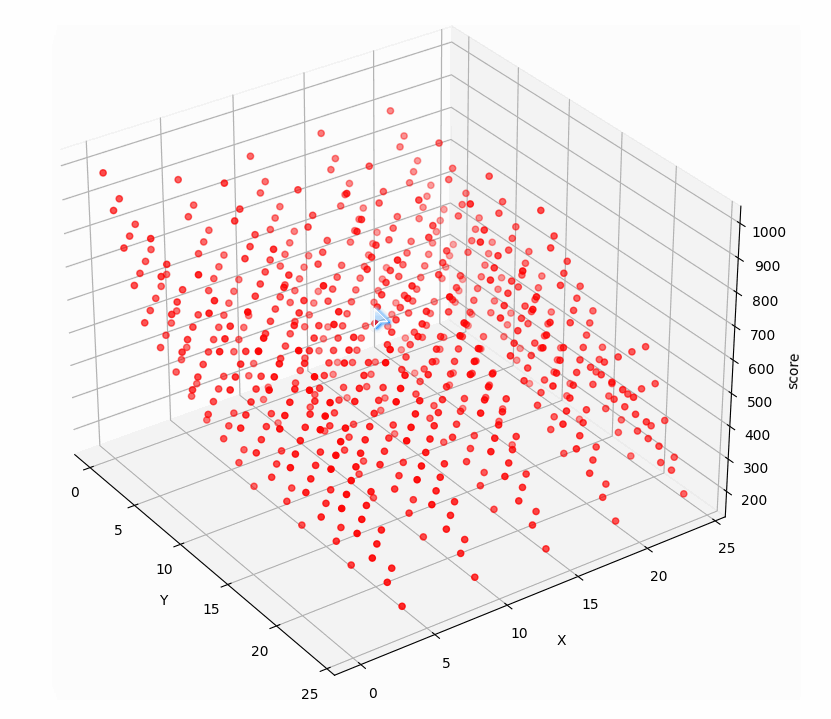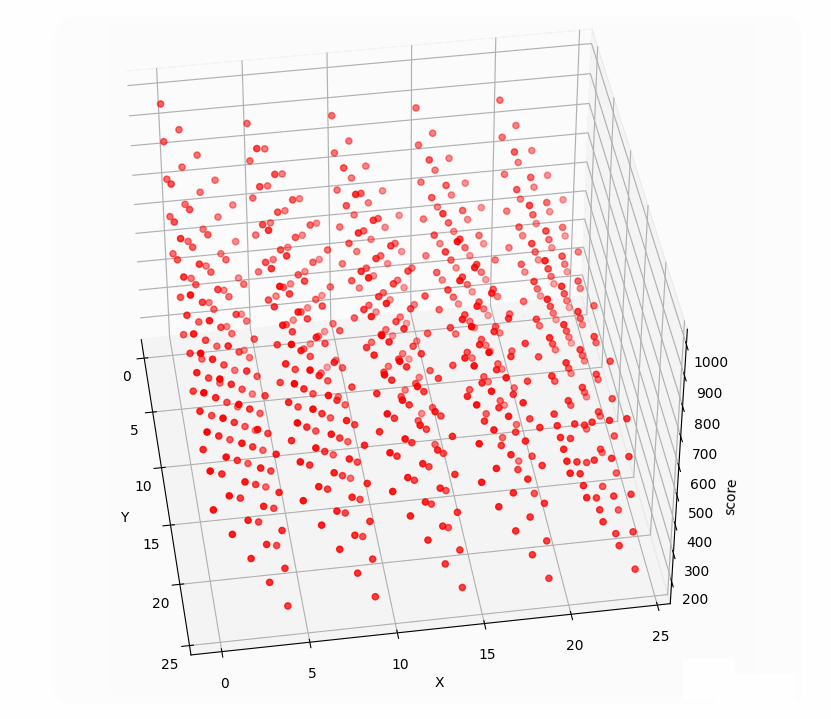
前两步点击与所得分数构成三维空间的点集，而点击十次有十个变量，与相应得分构成十一维空间点集，找十步的最高分相当于找十一维空间点集的最大值。遗传算法正适合找高维空间点集最值。

简单介绍遗传算法

从名字来看，遗传算法借用了生物学里达尔文的进化理论：”适者生存，不适者淘汰“。
不断让种群玩游戏，分数高者易存活，这样一代代下去会不断逼近分数高的解。
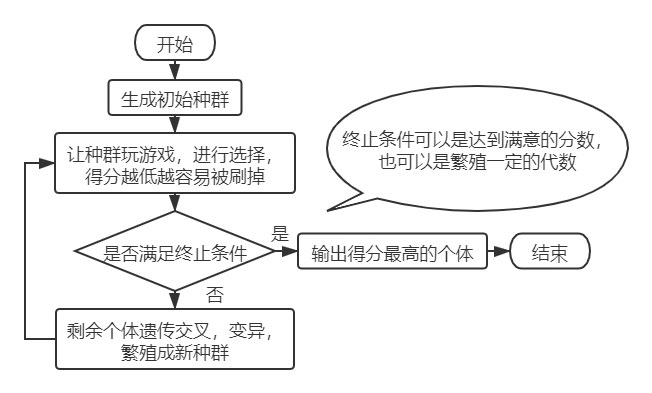
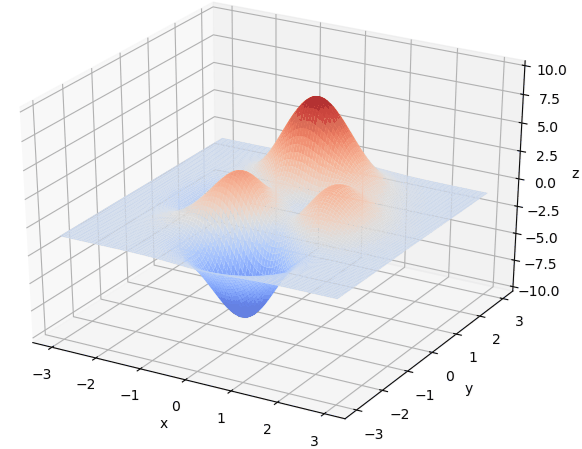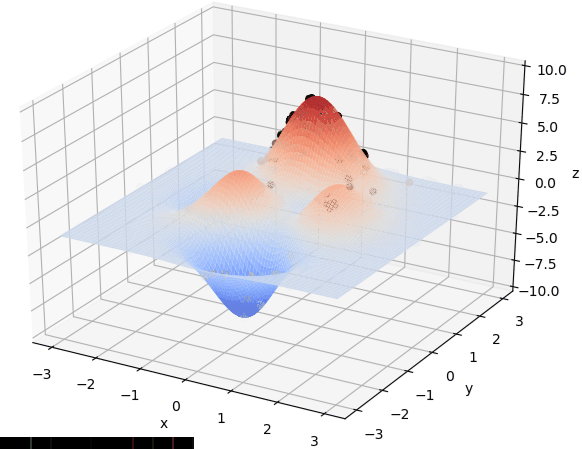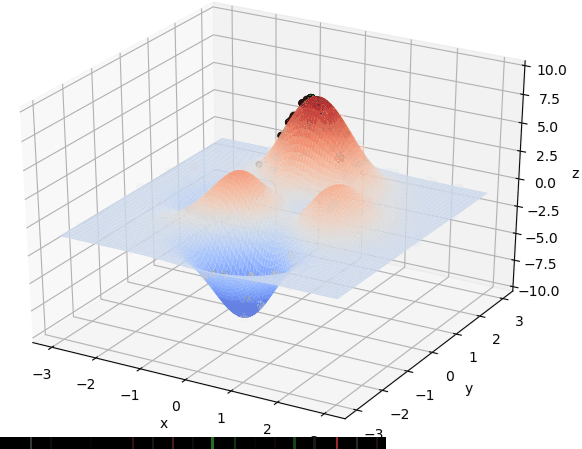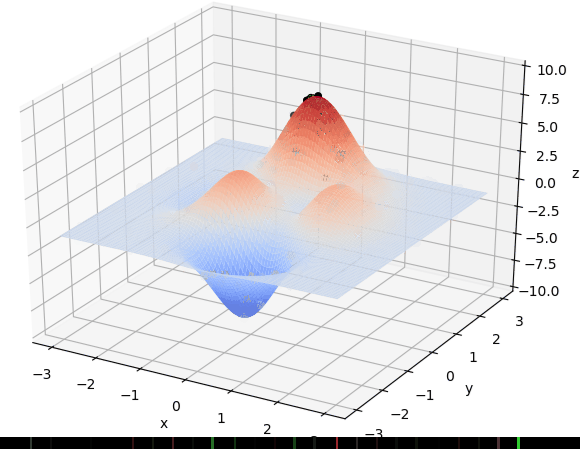
在这里插入图片描述
遗传算法找函数最值的直观图解：
图中可见初始种群遍布整张图，越高越易存活，随着一次次迭代，种群越爬越高，最终逼近函数最大值。gif图出处
同样可以用这种方法找十步万度的高维空间点集最值。
在这里插入图片描述

遗传算法的实现包括：
基因，染色体： 染色体代表问题中的个体（可能的解），由若干基因组成。
适应度函数，选择： 不同的个体在环境中有不同的适应度，通过适应度函数得到。适应度决定个体的存活几率，是选择的重要依据。
遗传交叉： 互换染色体某些位上的基因。
变异： 基因突变成其他值。
依据适应度选择，存活的个体随机进行遗传交叉变异，如此反复。这些过程都可以用代码实现，但没必要，因为python有遗传算法库，网上有很多教程安装GA算法开发包scikit-opt，不赘叙。

通过遗传算法库只需确定自变量个数和范围，适应度函数，种群数量和最大迭代次数即可，具体算法过程封装在库里。
自变量个数：玩家点击次数
自变量取值范围：自变量在指针编码里取值，所以自变量范围与指针个数有关，pNum个指针时，取值范围是0到pNum-1
适应度函数demo_func：操作数组表示个体，游戏得分即个体的适应度。
种群数量和迭代次数可以自己更改尝试。
在这里插入图片描述
但python的scikit-opt遗传算法库demo_func返回值越小个体越易存活，而十步万度要求最高分，所以适应度函数是得分的倒数。

def demo_func(p): # 计算个体p的适应度
    return 1 / Game.star(map, index, p)  # 这个遗传算法库适应度越小p越易存活，要求最高分，所以取游戏得分的倒数

贪心

贪心策略：玩家每次点击前都会预判所有情况，从中选出得分最高的，每步都是当前看来最好的选择。

'''贪心'''
def greedNext(now): 		 # 当前是now，返回下一步的最优选择
    gScore = 0
    for next in range(pNum): # 遍历下一步的所有情况，t: try or temp
        tOperat = now + [next]
        tScore = Game.star(map, index, tOperat)
        # print("if click ", next, " then score: ", tScore)
        if(tScore > gScore): # 得到得分最高的那步
            gScore = tScore
            best_next = next
    # print("so click: ", best_next)
    return [best_next]

gOperat = []                      # 存贪心所得的解
for i in range(clickNum):         # 添加clickNum个元素
    gOperat += greedNext(gOperat) # 每次添加局部最优解
print('贪心得到最优解: ', gOperat, ' score:  ', Game.star(map, index, gOperat), '\n')

但事实再次证明了每次局部最优不能代表全局最优。
例如第一关用贪心得到1800，但第一关最高分应该是 2070 如 [0 1 1 2 1 2 1 3 0 0]，而在难度高的关卡里贪心甚至不如随机。
在这里插入图片描述
这种贪心策略是每次遍历当前下一步的所有情况，从中选出得分最高的那步。
进一步，可以每次遍历下两步所有情况，从中选择得分最高的两步……每次遍历接下来n步所有情况从中选择得分最高的n步。当有pNum个指针时，每次贪心遍历n步就要从pNum的n次方种情况中选最优组合。
例如：一次贪心遍历四步

def greedNext4(now):          # 当前是now，返回当前后四步的最优选择
    gScore = 0
    for next1 in range(pNum): # 遍历后面第四步所有情况
        for next2 in range(pNum):         
            for next3 in range(pNum):     
                for next4 in range(pNum): 
                    tOperat = now + [next1, next2, next3, next4]
                    tScore = Game.star(map, index, tOperat)
                    # print("if click ", next1, ",", next2, ",", next3, ",", next4, " then score: ", tScore)
                    if(tScore > gScore): # 选出得分最高的组合
                        gScore = tScore
                        best_next = [next1, next2, next3, next4]
    # print("so click: ", best_next)
    return best_next

遗传+贪心

贪心多次不一定达到最优解，但贪心一次一定能达到当前的最优解。
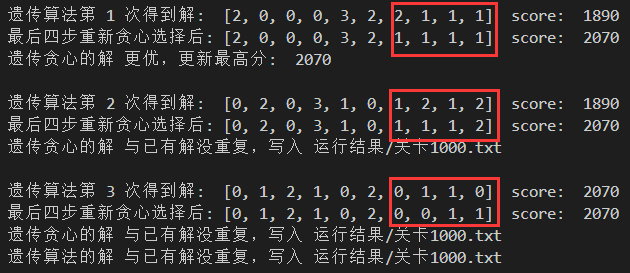
在得到遗传算法的解后，删掉最后n步，贪心遍历最后n步所有情况选择最优解。
在遗传算法解的基础上能保证最后n步是最优的，n自然是越大越好，但时间复杂度也是指数级增加的，所以n的取值需要与遗传算法权衡。当遗传算法容易找到满意解时，n可以取值小甚至不用贪心，当遗传算法比较难找到时n就可以取大一点。
如图，红框是对遗传算法的解最后四步重新贪心选择。
遗传贪心运行结果

三、最后

标准答案

最后看到有人用一个很巧妙的结论遍历出了所有非随机关卡的最优解。
十步万度每关最优解
该结论是：十步万度的最终局面、总度数只和每个圈的点击次数有关，而跟点击它们的顺序无关。
如果先点a再点b，跟先点b再点a的结果是一模一样的。
这样就可以在遍历的时候少遍历很多情况。

算法的优势与不足

我用遗传算法得到的解跟他遍历出来的最优解比较，发现只有2，3关难度比较高的解离最优解还差点，其余所有关卡用遗传算法得到的解就是最优解。说明遗传算法解这个游戏还算可行。

不足：
1、因为用的遗传算法库，所以很多东西都封装在库里，不好自己调试。
2、十步万度就前两步的三维点集来看，可能的次优解太多了，而且最优解不一定是像爬山那样慢慢爬上去，而是在可能某个普通的地方突然跃上去，所以遗传算法不一定是解十步万度特别好的方法。

遗传算法寻找最优解直观演示如图：
在这里插入图片描述
十步万度中前两步在空间中的点集如图，是有许多局部最优解的：

优势：
就算用上面那个标准答案的结论，遍历的样本空间还是很大，假设关卡里有pNum个指针，玩家可以点击clickNum次，复杂度仍是O(pNum ^ clickNum)
而遗传算法搜索的样本空间是种群数量 * 迭代次数，显然遗传算法搜索的更少。
所以遗传算法能花相对小的搜索代价找到较优的解。