一、前言
暴力递归和动态规划的本质是一样的,动态规划就是尝试减少重复计算的技巧而已。这种技巧是一个大型套路,先写出用尝试的思路解决问题的递归函数,而不用操心时间复杂度。(这个过程是无可替代的,没有套路的,只能依靠个人智慧,或者足够多的经验)
动态规划的优化大致分为三个过程,第一阶段是暴力递归,即不使用任何技巧优化时间复杂度,目的仅仅是通过尝试得到正确的递归函数;第二阶段是记忆化搜索, 即将前面计算得到结果记录下来,从而避免后续重复计算造成的超时问题;第三阶段是严格表结构,即采用斜率优化等数学模型来优化时间和空间复杂度,是一种高级的动态规划。
但是怎么把尝试的版本,优化成动态规划,是有固定套路的,大体步骤如下
- 找到什么可变参数可以代表一个递归状态,也就是哪些参数一旦确定,返回值就确定了
- 把可变参数的所有组合映射成一张表,有 1 个可变参数就是一维表,2 个可变参数就 是二维表,......
- 最终答案要的是表中的哪个位置,在表中标出
- 根据递归过程的 base case,把这张表的最简单、不需要依赖其他位置的那些位置填好值
- 根据递归过程非base case的部分,也就是分析表中的普遍位置需要怎么计算得到,那 么这张表的填写顺序也就确定了
- 填好表,返回最终答案在表中位置的值
二、机器人到达指定位置的方法数量
2.1 问题介绍
【题目】 假设有排成一行的 N 个位置,记为 1~N(N 一定大于或等于 2)。开始时机器人在其中的 M 位置上(M 一定在 1~N 中),机器人可以往左走或者往右走,如果机器人来到 1 位置, 那么下一步只能往右来到 2 位置;如果机器人来到 N 位置,那么下一步只能往左来到 N-1 位置。 规定机器人必须走 K 步,最终能来到 P 位置(P 也一定在1~N 中)的方法有多少种。给 定四个参数 N、M、K、P,返回方法数。
【举例】 N=5,M=2,K=3,P=3。上面的参数代表所有位置为 1 2 3 4 5。机器人最开始在 2 位置上,必须经过 3 步,最后到 达 3 位置。走的方法只有如下 3 种:
- 从2到1,从1到2,从2到3
- 从2到3,从3到2,从2到3
- 从2到3,从3到4,从4到3
所以返回方法数 3。
N=3,M=1,K=3,P=3 上面的参数代表所有位置为 1 2 3。机器人最开始在 1 位置上,必须经过 3 步,最后到达 3 位置。怎么走也不可能,所以返回方法数 0。
2.2 解题思路
2.2.1 暴力尝试
首先用尝试的方法写出暴力递归函数f,f的返回值为方法数。暴力递归之所以暴力,是因为它遇到每一种情况时都需要分析能导致这种情况的子情况。例如 f(rest=4,cur=2) 时,需要调用 f(rest=3,cur=1)和f(rest=3,cur=3)这两种子情况,分析f(rest=3,cur=1)时又要调用f(rest=2,cur=2);分析f(rest=3,cur=3)时要调用f(rest=2,cur=2)和f(rest=2,cur=4)……到达底层以后再向上回溯汇总方法数。
这种调用方式是树型结构,需要耗费大量时间和空间。时间复杂度为.
//暴力递归:f函数返回方法数
//N是位置总数,P是最终位置,rest表示剩余步数,cur表示当前位置
int f1(int N, int P, int rest, int cur)
{
if (rest == 0)//base case 当步数走完,若在P点,返回一个结果
return cur == P ? 1 : 0;
if (cur == 1)//若在左边界,只能往右
return f1(N, P, rest - 1, 2);
if (cur == N)//若在有边界,只能往左
return f1(N, P, rest - 1, N - 1);
//在中间位置时,有向左和向右两种选择
return f1(N, P, rest - 1, cur - 1) + f1(N, P, rest - 1, cur + 1);
}2.2.2 记忆化搜索
分析暴力递归的情况我们很容易发现调用递归函数时,经常会发生重复计算的问题,上例中就发升了连续两次调用f(rest=2,cur=2)函数。所以如果能将这个函数的返回值记录下来,那么在下次调用时就可以节省大量时间。时间复杂度为.
使用dp数组来记录返回值,初始化数组为全“-1”,数组中的值记录每种情况下的方法数。
int dp[100][100];
int walkWay(int N, int P, int K, int M)
{
for (int i = 0; i <= K; i++)
{
for (int j = 0; j <= N; j++)
dp[i][j] = -1;
}
return f2(N, P, K, M);
}
int f2(int N, int P, int rest, int cur)
{
if (dp[rest][cur] != -1)//缓存命中,直接返回方法数
return dp[rest][cur];
//缓存未命中,记录
if (rest==0)//base case
{
dp[rest][cur] = cur == P ? 1 : 0;
return dp[rest][cur];
}
//有路可以继续走
if (cur == 1)
{
dp[rest][cur] = f2(N, P, rest - 1, cur + 1);
return dp[rest][cur];
}
if (cur == N)
{
dp[rest][cur] = f2(N, P, rest - 1, cur - 1);
return dp[rest][cur];
}
dp[rest][cur] = f2(N, P, rest - 1, cur - 1) + f2(N, P, rest - 1, cur + 1);
return dp[rest][cur];
}2.2.3 严格表结构的动态规划

通过递归的对应关系,很容易列出dp数组的每一个元素。如图所示,当从2出发,走4步到达4位置的走法共有4种。这张dp表就是严格表结构。严格表结构的时间复杂度显然是填表的时间
严格表结构和记忆化搜索最大的区别是:记忆化搜索时不用整理数据间的依赖关系,只需要列出递归函数,并用dp表记录递归函数的返回值即可;严格表结构中则需要弄清楚位置间依赖的顺序。
弄清楚了位置间的依赖关系,就不需要使用递归函数了,直接按照依赖关系正序填表即可。动态规划的核心不在于状态转换方程,而是在于明确表结构中元素位置的依赖关系。
2.3 代码实现
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int dp[100][100];
int dpWay(int N, int P, int K, int M)
{
dp[0][P] = 1;
for (int rest = 1; rest <= K; rest++)
{
for (int cur = 1; cur <= N; cur++)
{
if (cur == 1)
dp[rest][cur] = dp[rest - 1][cur + 1];
else if (cur == N)
dp[rest][cur] = dp[rest - 1][cur - 1];
else dp[rest][cur] = dp[rest - 1][cur - 1] + dp[rest - 1][cur + 1];
}
}
return dp[K][M];
}
int main()
{
int N = 5, P = 4, M = 2, K = 4;
cout << dpWay(N, P, K, M);
}
三、换钱的最少货币数(01背包 和 完全背包)
3.1 问题介绍
3.1.1 01背包
【题目】 给定数组arr,arr中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币只可以使用一次,再给定一个整数 aim,代表要找的钱数,求组成 aim 的最少货币数。 【举例】 arr=[5,10,2,3],aim=20。可以发现,只有选择所有硬币才能满足题目要求,所有返回值为4.
3.1.2 完全背包
【题目】 给定数组arr,arr中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数 aim,代表要找的钱数,求组成 aim 的最少货币数。 【举例】 arr=[5,2,3],aim=20。4 张 5 元可以组成 20 元,其他的找钱方案都要使用更多张的货币,所以返回 4。 arr=[5,2,3],aim=0。 不用任何货币就可以组成 0 元,返回 0。 arr=[3,5],aim=2。 根本无法组成 2 元,钱不能找开的情况下默认返回-1。
3.2 解题思路和代码实现
首先完全背包问题和0-1背包的不同之处在于:0-1背包每一件物品只能被装一次;完全背包可以无限制的装,物品数量没有限制。所以01背包和完全背包体现在代码实现上最大的区别就是01背包有2个分支:要当前物品,不要当前物品;而完全背包有3个分支:要当前物品1次,要当前物品多次,不要当前物品。
3.2.1 01背包
使用从暴力递归到动态规划的思路来完成。本题的base case为还未凑到的钱小于等于0(小于0时意味着此路不通;等于0时意味着找到了一个解决方式)。
要当前物品的分支:指针index加一,指向下一个货币,同时rest减去当前货币面值。
不要当前物品的分支:指针index加一,指向下一个货币,rest不变。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
//n是硬币数量;arr是硬币列表,都是固定参数
//index变量用于遍历arr数组,选择硬币;rest表示还未凑到的钱
//返回解决问题所需的最少硬币数
int process1(int n, int arr[], int index, int rest)
{
if (rest < 0)//出现负钱数,这条路肯定走不通
return -1;
if (rest == 0)//凑够了,所以还需要0枚硬币
return 0;
//rest > 0 but 没硬币
if (index == n)//将所有硬币都选了一遍,还没凑齐,这条路不通
return -1;
//rest > 0 and 有硬币
//分为要这个硬币和不要两种情况考虑
int p1 = process1(n, arr, index + 1, rest);
int p2Next = process1(n, arr, index + 1, rest - arr[index]);//要了以后指针就指向下一个物品了
if (p1 == -1 && p2Next == -1)
return -1;
else
{
if (p1 == -1)
return p2Next + 1;
if (p2Next == -1)
return p1;
return min(p1, p2Next + 1);
}
}
//严格表结构的动态规划
int dp[10005][5005];//横轴为rest,纵轴为index
int process2(int n, int arr[], int aim)
{
for (int row = 0; row <= n; row++)
dp[row][0] = 0;//当rest=0时,凑够了,还需要0枚硬币
for (int col = 1; col <= aim; col++)
dp[n][col] = -1;//当index=n,但这条路不rest!=0时,说明通
//从下往上,因为index较大的位置先确定
for (int index = n - 1; index >= 0; index--)
{
for (int rest = 1; rest <= aim; rest++)
{
int p1 = dp[index + 1][rest];//不要
int p2Next = -1;//避免数组越界
if (rest - arr[index] >= 0)//要
p2Next = dp[index + 1][rest - arr[index]];
if (p1 == -1 && p2Next == -1)
dp[index][rest] = -1;
else
{
if (p1 == -1)
dp[index][rest] = p2Next + 1;//又拿了一个硬币
else if (p2Next == -1)
dp[index][rest] = p1;
else
dp[index][rest] = min(p1, p2Next + 1);
}
}
}
return dp[0][aim];
}
int main()
{
int n = 5;
int arr[5] = { 1,5,10,20,50 };
int aim = 100;
cout << process1(n, arr, 0, aim);
}
3.2.2 完全背包
使用从暴力递归到动态规划的思路来完成。本题的base case为还未凑到的钱小于等于0(小于0时意味着此路不通;等于0时意味着找到了一个解决方式)。
要当前物品1次的分支:指针index加一,指向下一个货币,同时rest减去当前货币面值。
要当前物品多次的分支:index不变,rest减去当前货币面值,下次判断时可以继续选择该物品。
不要当前物品的分支:指针index加一,指向下一个货币,rest不变。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
//n是硬币数量;arr是硬币列表,都是固定参数
//index变量用于遍历arr数组,选择硬币;rest表示还未凑到的钱
//返回解决问题所需的最少硬币数
int process1(int n, int arr[], int index, int rest)
{
if (rest < 0)//出现负钱数,这条路肯定走不通
return -1;
if (rest == 0)//凑够了,所以还需要0枚硬币
return 0;
//rest > 0 but 没硬币
if (index == n)//将所有硬币都选了一遍,还没凑齐,这条路不通
return -1;
//rest > 0 and 有硬币
//分为要这个硬币和不要两种情况考虑
int p1 = process1(n, arr, index + 1, rest);
int p2Next = process1(n, arr, index, rest - arr[index]);//要了以后还可以继续要
if (p1 == -1 && p2Next == -1)
return -1;
else
{
if (p1 == -1)
return p2Next + 1;
if (p2Next == -1)
return p1;
return min(p1, p2Next + 1);
}
}
//严格表结构的动态规划
int dp[10005][5005];//横轴为rest,纵轴为index
int process2(int n, int arr[], int aim)
{
for (int row = 0; row <= n; row++)
dp[row][0] = 0;//当rest=0时,凑够了,还需要0枚硬币
for (int col = 1; col <= aim; col++)
dp[n][col] = -1;//当index=n,但这条路不rest!=0时,说明通
//从下往上,因为index较大的位置先确定
for (int index = n - 1; index >= 0; index--)
{
for (int rest = 1; rest <= aim; rest++)
{
int p1 = dp[index + 1][rest];//不要
int p2Next = -1;//避免数组越界
if (rest - arr[index] >= 0)//要
p2Next = dp[index][rest - arr[index]];
if (p1 == -1 && p2Next == -1)
dp[index][rest] = -1;
else
{
if (p1 == -1)
dp[index][rest] = p2Next + 1;//又拿了一个硬币
else if (p2Next == -1)
dp[index][rest] = p1;
else
dp[index][rest] = min(p1, p2Next + 1);
}
}
}
return dp[0][aim];
}
int main()
{
int n = 5;
int arr[5] = { 1,5,10,20,50 };
int aim = 100;
cout << process1(n, arr, 0, aim);
}
四、纸牌游戏
4.1 问题介绍
给定一个整型数组arr,代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸 牌,规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左或最右的纸牌,玩家A 和玩家B都绝顶聪明。请返回最后获胜者的分数。
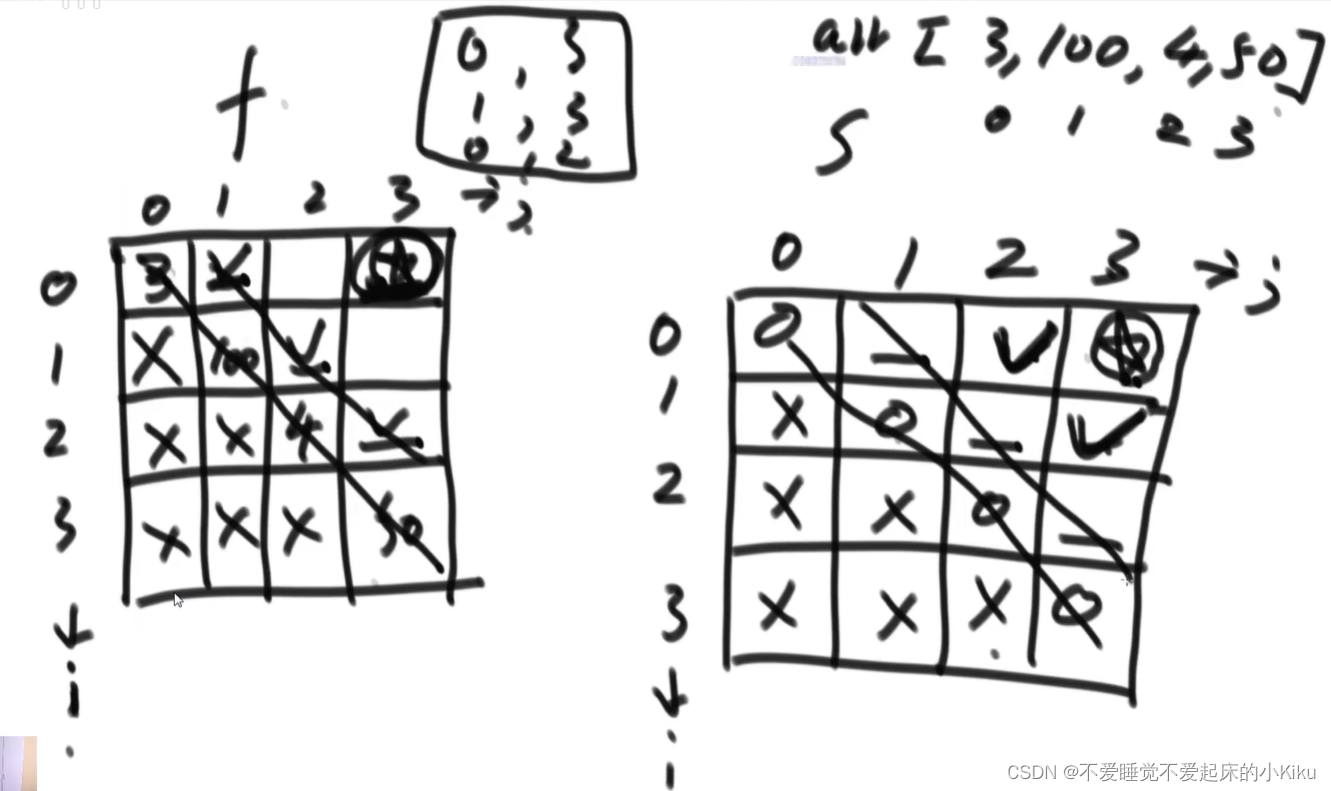
【举例】 arr=[1,2,100,4]。 开始时,玩家A只能拿走1或4。如果开始时玩家A拿走1,则排列变为[2,100,4],接下来 玩家 B可以拿走2或4,然后继续轮到玩家A... 如果开始时玩家A拿走4,则排列变为[1,2,100],接下来玩家B可以拿走1或100,然后继 续轮到玩家A... 玩家A作为绝顶聪明的人不会先拿4,因为拿4之后,玩家B将拿走100。所以玩家A会先拿1, 让排列变为[2,100,4],接下来玩家B不管怎么选,100都会被玩家 A拿走。玩家A会获胜, 分数为101。所以返回101。 arr=[1,100,2]。 开始时,玩家A不管拿1还是2,玩家B作为绝顶聪明的人,都会把100拿走。玩家B会获胜, 分数为100。所以返回100。
4.2 解题思路
4.2.1 暴力递归
前面的博客里详细讲过,在此不赘述。
链接如下:纸牌游戏暴力递归解法
4.2.2 动态规划
第一步:画出严格表结构图
先手函数 f 和后手函数 s 分别列表,横轴为 j ,纵轴为 i ,严格表表示为dp[ i ][ j ]。由于 i 为左指针, j 为右指针,所以 i 始终小于等于 j ,因此表的左下半部分没有实际意义。
第二步:确定base case
先手函数:显然当 i 和 j 重合时,只剩下一张牌未被选,因此我选择该牌并结束递归,返回arr[i]的值。所以表中对角线(i==j)上的值为arr[ ]中的值。
后手函数:显然当 i 和 j 重合时,只剩下一张牌未被选,因此对手会选择该牌并结束递归,后续我无法继续拿牌,返回0。所以表中对角线(i==j)上的值为0。
第三步:确定位置间的依赖关系
通过递归函数我们可以知道,f 函数中 f[ i ][ j ]的值依赖于arr[ i ]+s[ i+1 ][ j ]和 arr[ j ]+s[ i ][ j-1 ]中较大的一项,所以很容易知道本题的动态规划表应该沿对角线方向斜着填,此外由于填入的第一组数必须依赖base case(也就是对角线上的数),所以应该从左下角向右上角填写。
4.3 代码实现
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int f[101][101];
int s[101][101];
int dp(int arr[], int n)
{
if (arr == NULL || n == 0)//数组空,直接结束
return 0;
for (int i = 0; i < n; i++)//先按照base case填充对角线
f[i][i] = arr[i];
int row = 0, col = 1;//越过对角线开始
while (col < n)//按对角线填写严格表结构
{
int i = row;
int j = col;
while (i < n && j < n)
{
f[i][j] = max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
s[i][j] = min(f[i + 1][j], f[i][j - 1]);
i++, j++;
}
col++;
}
return max(f[0][n - 1], s[0][n - 1]);
}
int main()
{
int arr[] = { 1,2,100,4 };
cout << dp(arr, 4);
}
五、象棋中马的跳法
5.1 问题介绍
请同学们自行搜索或者想象一个象棋的棋盘,然后把整个棋盘放入第一象限,棋盘的最左下角是(0,0)位置。那么整个棋盘就是横坐标上9条线、纵坐标上10条线的一个区域。给你三个参数(x,y,k),返回如果 “马” 从(0,0)位置出发,必须走k步,最后落在(x,y)上的方法数有多少种?
5.2 解题思路
5.2.1 暴力递归
将问题分治,从远点跳 k 步到达(x,y)处,所以要先求跳 k-1 步能到达的某个位置(a,b),使得再跳一步就能到(x,y)处;然后求跳 k-2 步能到达的某个位置,使得再跳一步就能到(a,b)处,以此类推即可。
当步数为0时判断是否回溯到起点,如果没有则返回0种解决方式;若棋子越界,返回0种方法。
//从(0,0)出发,要去往(x,y)位置,必须跳step步,返回方法数
int process(int x, int y, int step)
{
//base case:越界and无步数
if (x < 0 || x>8 || y < 0 || y>9)
return 0;//0种方法,意为无法到达
if (step == 0)//步数用完了,不能动了
//相当于从终点往前推,如果步数没了,但是还没回到原点,说明此路不通
return (x == 0 && y == 0) ? 1 : 0;
//普遍情况:从其他每个位置跳到(x,y)的方法数
return process(x - 1, y + 2, step - 1)
+ process(x + 1, y + 2, step - 1)
+ process(x + 2, y + 1, step - 1)
+ process(x + 2, y - 1, step - 1)
+ process(x + 1, y - 2, step - 1)
+ process(x - 1, y - 2, step - 1)
+ process(x - 2, y - 1, step - 1)
+ process(x - 2, y + 1, step - 1);
}5.2.2 动态规划
由于有三个变量,所以使用三维dp数组。显然可以发现step层的取值必须依赖step-1层,所以从下向上来填表;行和列的先后次序任意,因为上层表的取值完全取决于下层表,和本层其他元素没有关系。
base case:在step=0层中,只有(0,0,0)的取值为1,意为马完全不动,其余都是0。
int dp[9][10][100];
//为了避免数组越界
int getvalue(int row, int col, int step)
{
if (row < 0 || row>8 || col < 0 || col>9)
return 0;
return dp[row][col][step];
}
int process2(int x, int y, int step)
{
//base case:越界
if (x < 0 || x > 8 || y < 0 || y > 9)
return 0;//0种方法,意为无法到达
dp[0][0][0] = 1;//第0层(step=0)只有不动的情况下为1,其余为0
for (int h = 1; h <= step; h++)
{
for (int r = 0; r < 9; r++)
{
for (int c = 0; c < 10; c++)
{
//将周围八个可以到达的点所对应的全部情况相加
dp[r][c][h] += getvalue(r - 1, c + 2, h - 1);
dp[r][c][h] += getvalue(r + 1, c + 2, h - 1);
dp[r][c][h] += getvalue(r + 2, c + 1, h - 1);
dp[r][c][h] += getvalue(r + 2, c - 1, h - 1);
dp[r][c][h] += getvalue(r + 1, c - 2, h - 1);
dp[r][c][h] += getvalue(r - 1, c - 2, h - 1);
dp[r][c][h] += getvalue(r - 2, c - 1, h - 1);
dp[r][c][h] += getvalue(r - 2, c + 1, h - 1);
}
}
}
return dp[x][y][step];
}5.3 代码实现
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
//从(0,0)出发,要去往(x,y)位置,必须跳step步,返回方法数
int process1(int x, int y, int step)
{
//base case:越界and无步数
if (x < 0 || x > 8 || y < 0 || y > 9)
return 0;//0种方法,意为无法到达
if (step == 0)//步数用完了,不能动了
//相当于从终点往前推,如果步数没了,但是还没回到原点,说明此路不通
return (x == 0 && y == 0) ? 1 : 0;
//普遍情况:从其他每个位置跳到(x,y)的方法数
return process1(x - 1, y + 2, step - 1)
+ process1(x + 1, y + 2, step - 1)
+ process1(x + 2, y + 1, step - 1)
+ process1(x + 2, y - 1, step - 1)
+ process1(x + 1, y - 2, step - 1)
+ process1(x - 1, y - 2, step - 1)
+ process1(x - 2, y - 1, step - 1)
+ process1(x - 2, y + 1, step - 1);
}
int dp[9][10][100];
//为了避免数组越界
int getvalue(int row, int col, int step)
{
if (row < 0 || row>8 || col < 0 || col>9)
return 0;
return dp[row][col][step];
}
int process2(int x, int y, int step)
{
//base case:越界
if (x < 0 || x > 8 || y < 0 || y > 9)
return 0;//0种方法,意为无法到达
dp[0][0][0] = 1;//第0层(step=0)只有不动的情况下为1,其余为0
for (int h = 1; h <= step; h++)
{
for (int r = 0; r < 9; r++)
{
for (int c = 0; c < 10; c++)
{
//将周围八个可以到达的点所对应的全部情况相加
dp[r][c][h] += getvalue(r - 1, c + 2, h - 1);
dp[r][c][h] += getvalue(r + 1, c + 2, h - 1);
dp[r][c][h] += getvalue(r + 2, c + 1, h - 1);
dp[r][c][h] += getvalue(r + 2, c - 1, h - 1);
dp[r][c][h] += getvalue(r + 1, c - 2, h - 1);
dp[r][c][h] += getvalue(r - 1, c - 2, h - 1);
dp[r][c][h] += getvalue(r - 2, c - 1, h - 1);
dp[r][c][h] += getvalue(r - 2, c + 1, h - 1);
}
}
}
return dp[x][y][step];
}
int main()
{
cout << process1(7, 7, 10);//515813
cout << process2(7, 7, 10);
}六、Bob的生存概率
6.1 问题介绍
给定五个参数n,m,i,j,k。表示在一个n*m的区域,Bob处在(i,j)点,每次Bob等概率的向上、 下、左、右四个方向移动一步,Bob必须走k步。如果走完之后,Bob还停留在这个区域上, 就算Bob存活,否则就算Bob死亡。请求解Bob的生存概率,返回字符串表示分数的方式。
6.2 解题思路
先求出Bob在走k步条件下存活的可能数,然后求出所有的可能数,二者相除即可。
6.3 代码实现
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
long gcd(int a, int b)
{
int tmp;
while (b > 0)
{
tmp = a % b;
a = b;
b = tmp;
}
return a;
}
//N*M的区域,从(row,col)出发,继续走rest步,返回生存方法数
long process1(int N, int M, int row, int col, int rest)
{
//正常情况下范围为0~N-1,0~M-1;若越界,直接返回0种生存方法
if (row < 0 || row == N || col < 0 || col == M)
return 0;
if (rest == 0)//没越界并且走完了,那么活下来了
return 1;
//没走完,也还没越界
long live = process1(N, M, row - 1, col, rest - 1);//向上
live += process1(N, M, row + 1, col, rest - 1);//向下
live += process1(N, M, row, col - 1, rest - 1);//向左
live += process1(N, M, row, col + 1, rest - 1);//向右
return live;
}
void Bob1(int N, int M, int row, int col, int k)
{
long live = process1(N, M, row, col, k);//活下来可能性
long all = (long)pow(4, k);//所有可能性
long gcd1 = gcd(all, live);
printf("%ld/%ld\n", live / gcd1, all / gcd1);
}
int dp[100][100][100] = { 0 };
long process2(int N, int M, int row, int col, int k)
{
//正常情况下范围为0~N-1,0~M-1;若越界,直接返回0种生存方法
if (row <= 0 || row > N || col <= 0 || col > M)
return 0;
//base case: 没步数了,并且还在范围内
for (int i = 1; i <= N; i++)
for (int j = 1; j <= M; j++)
dp[i][j][0] = 1;
for (int rest = 1; rest <= k; rest++)
{
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
dp[i][j][rest] += dp[i - 1][j][rest-1];
dp[i][j][rest] += dp[i + 1][j][rest-1];
dp[i][j][rest] += dp[i][j + 1][rest-1];
dp[i][j][rest] += dp[i][j - 1][rest-1];
}
}
}
return dp[row + 1][col + 1][k];//为避免越界,整体移动一格
}
void Bob2(int N, int M, int row, int col, int k)
{
long live = process2(N, M, row, col, k);//活下来可能性
long all = (long)pow(4, k);//所有可能性
long gcd1 = gcd(all, live);
printf("%ld/%ld\n", live / gcd1, all / gcd1);
}
int main()
{
Bob1(9, 9, 3, 3, 10);
Bob2(9, 9, 3, 3, 10);
}七、找零方式
7.1 问题介绍
给定数组 arr,arr 中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数 aim,代表要找的钱数,求所有的找零方法有多少种。
7.2 解题思路
枚举法,列出使用某张钞票n次的所有可能。
7.2.1 暴力递归
int process1(int n,int arr[], int index, int rest)
{
if (index == n)
return rest == 0 ? 1 : 0;
int ways = 0;
//枚举选择每种货币zhang张的情况
for (int zhang = 0; arr[index] * zhang <= rest; zhang++)
ways += process1(n, arr, index + 1, rest - zhang * arr[index]);
return ways;
}7.2.2 动态规划
每一个位置都依赖它下面从左往右的位置。所有每行从左往右,整体从下往上。
int dp[100][100];
int process2(int n, int arr[], int aim)
{
if (arr == NULL || n == 0)
return 0;
dp[n][0] = 1;
for (int index = n - 1; index >= 0; index--)
{
for (int rest = 0; rest <= aim; rest++)
{
int ways = 0;
for (int zhang = 0; arr[index] * zhang <= rest; zhang++)
ways += dp[index + 1][rest - arr[index] * zhang];
dp[index][rest] = ways;
}
}
return dp[0][aim];
}7.2.3 斜率优化
通过观察得知,使用枚举的方法存在大量重复计算,例如arr[ i ]=3时,dp[3][12]=dp[4][12]+dp[4][9]+dp[4][6]+dp[4][3]+dp[4][0];而dp[3][15]=dp[4][15]+dp[4][12]+dp[4][9]+dp[4][6]+dp[4][3]+dp[4][0]。我们很容易化简为dp[3][15] = dp[4][15]+dp[3][12].
//斜率优化:如果填表时有枚举行为,那么判断能否用临近的值代替枚举的过程
int process3(int n, int arr[], int aim)
{
if (arr == NULL || n == 0)
return 0;
dp[n][0] = 1;
for (int index = n - 1; index >= 0; index--)
{
for (int rest = 0; rest <= aim; rest++)
{
dp[index][rest] = dp[index + 1][rest];//继承不拿的情况
if (rest - arr[index] >= 0)
dp[index][rest] += dp[index][rest - arr[index]];
}
}
return dp[0][aim];
}7.3 代码实现
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int process1(int n,int arr[], int index, int rest)
{
if (index == n)
return rest == 0 ? 1 : 0;
int ways = 0;
//枚举选择每种货币zhang张的情况
for (int zhang = 0; arr[index] * zhang <= rest; zhang++)
ways += process1(n, arr, index + 1, rest - zhang * arr[index]);
return ways;
}
int dp[100][100];
int process2(int n, int arr[], int aim)
{
if (arr == NULL || n == 0)
return 0;
dp[n][0] = 1;
for (int index = n - 1; index >= 0; index--)
{
for (int rest = 0; rest <= aim; rest++)
{
int ways = 0;
for (int zhang = 0; arr[index] * zhang <= rest; zhang++)
ways += dp[index + 1][rest - arr[index] * zhang];
dp[index][rest] = ways;
}
}
return dp[0][aim];
}
//斜率优化:如果填表时有枚举行为,那么判断能否用临近的值代替枚举的过程
int process3(int n, int arr[], int aim)
{
if (arr == NULL || n == 0)
return 0;
dp[n][0] = 1;
for (int index = n - 1; index >= 0; index--)
{
for (int rest = 0; rest <= aim; rest++)
{
dp[index][rest] = dp[index + 1][rest];//继承不拿的情况
if (rest - arr[index] >= 0)
dp[index][rest] += dp[index][rest - arr[index]];
}
}
return dp[0][aim];
}
int main()
{
int n = 5;
int arr[5] = { 1,5,10,20,50 };
int aim = 100;
cout << process1(n, arr, 0, aim) << endl;
cout << process2(n, arr, aim) << endl;
cout << process3(n, arr, aim) << endl;
}






















 507
507











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








