Polya Counting

Polya 计数的主要思想是对着色方案进行分类。
对一个图形进行某种操作（旋转或翻转）后，看不出任何变化。这样的操作只有有限个（从效果上看）。
如：一个对正方形的操作只可能有以下几种，

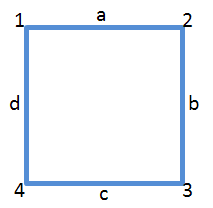
ρ1：逆时针翻转  90°
ρ2：逆时针翻转180°
ρ3：逆时针翻转270°
ρ4：逆时针翻转360°（相当于不动）
τ1：沿a、c中点翻转
τ2：沿b、d中点翻转
τ3：沿1、3对角线翻转
τ4：沿2、4对角线翻转

现在，我们把这些操作表示成一一对应的形式(permutation)
ρ1：逆时针翻转  90°

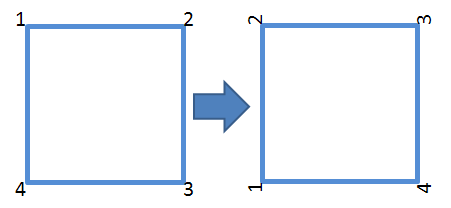
          (1 2 3 4)
              ↓
          (2 3 4 1)

ρ2：逆时针翻转180°

          (1 2 3 4)
              ↓
          (3 4 1 2)

ρ3：逆时针翻转270°

          (1 2 3 4)
              ↓
          (4 1 2 3)

ρ4：逆时针翻转360°

          (1 2 3 4)
              ↓
          (1 2 3 4)

τ1：沿a、c中点翻转

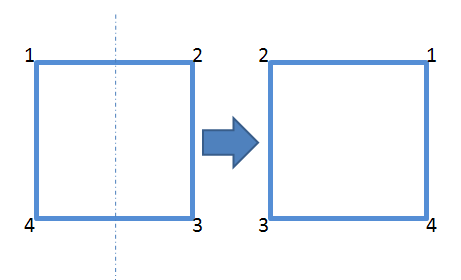
          (1 2 3 4)
              ↓
          (2 1 4 3)

τ2：沿b、d中点翻转

          (1 2 3 4)
              ↓
          (4 3 2 1)

τ3：沿1、3对角线翻转

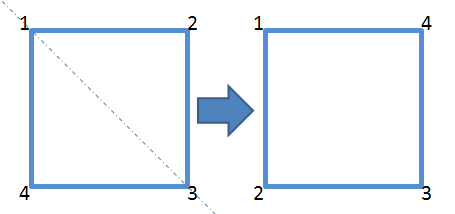
          (1 2 3 4)
              ↓
          (1 4 3 2)

τ4：沿2、4对角线翻转

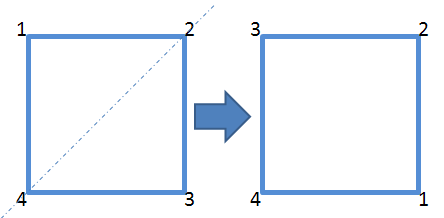
          (1 2 3 4)
              ↓
          (3 2 1 4)

回到着色问题上来，对某种着色方案c施以某种操作f后，得到一种新的方案f * c。但其实它们是同一种coloring。


先定义两个集合：
G(c) = {f: f in G, f * c = c}
G(c)是使得c不变的permutation集合。
如：


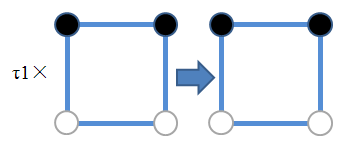
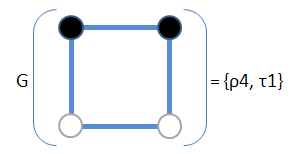
C(f) = {c: c in C, f * c = c}
C(f)是施以f后保持不变的coloring的集合。
如：

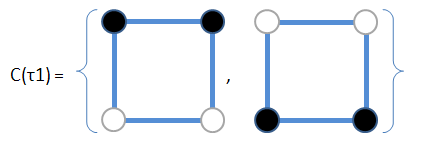
Polya 计数基于两个观察结果：
1.对任意一个permutation f，有且只有|G(c)|个permutation能够产生与f同样的效果。


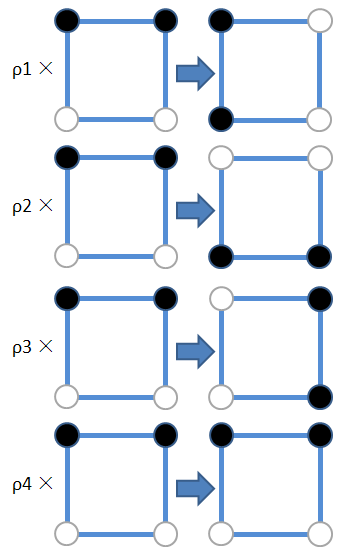
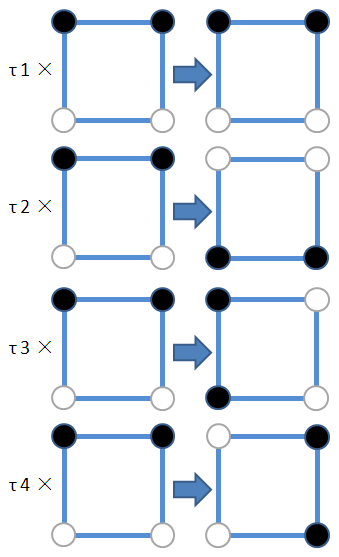
ρ1和τ3产生了同样的效果；
ρ2和τ2产生了同样的效果；
ρ3和τ4产生了同样的效果；
ρ4和τ1产生了同样的效果。
注意G(c) = {ρ4, τ1}，即   |G(c)| = 2。

2.每个permutaion能分成若干个集合(cycle)，每个整数只可能出现在一个集合里面。
其实，某个cycle中的元素在这次操作中处于对称的位置（只能着相同的颜色），而且这个cycle着什么色不影响其他cycle的着色。
如：permutaion
          (1 2 3 4)
             ↓
          (2 3 4 1)
只有一个cycle（1234），而
          (1 2 3 4)
             ↓
          (2 1 4 3)
有两个cycle，（12）（34）。

由规律1可以得出：
the number of colorings equivalent to c = |G| / |G(c)|

由规律2可以得出：
如果有k种颜色，permutaion f 能产生k^#种方案（#是f的cycle个数）

the number N(G, C) of nonequivalent colorings in C is：
    N(G, C) = ∑|G(c)| / |G|     (c ∈ C)
有兴趣的可以去看Richard A. Brualdi 的 Introductory Combinatorics。

用pku 1286 实践一下。
注意几个细节：
1.permutation f 中的每个整数至多属于因子分解（把f分解成cycle的乘积）中的一个cycle。
2.cycle内必须着相同的颜色，但一个cycle的着色不影响另一个cycle的着色。
3.对一个正n角形的顶点施加的操作只有2n个。一半为rotation，一半为reflection。
4.对一个正（2k）角形的顶点施加的操作中，有一半的reflection是由2个1-cycle和（k-1）个2-cycle构成，还有一半是由 k 个2-cycle构成。
5.对一个正（2k+1）角形的顶点施加的操作中，所有的reflection都是由1个1-cycle和 k 个2-cycle构成。
6.如果rotation ρ(n)包含一个t-cycle，根据对称性，它一定只包含t-cycle，即 t 是 n 的一个因子。

// 1286 Necklace of Beads # include <iostream> using namespace std; __int64 power(const __int64 a, const __int64 b) { __int64 r = a; __int64 m = b; if (m == 0) { return 1; } else if (m % 2 == 0) //m is even { return power(r * r, m / 2); } else //m is odd { return r * power(r * r, m / 2); } } __int64 necklace(int n) { __int64 rotation = 0; // 计算 rotation 的 cycle 数。 for (long i = 1; i <= n; ++i) { long d = 0; for (long j = 1; j <= n; ++j) { if (i * j % n == 0) { d = j; break; } } rotation += power(3, n / d); } if (n % 2 == 0) { __int64 k = n / 2; // 再加上 reflection 的 cycle 数。 return (rotation + k * power(3, k + 1) + k * power(3, k)) / (2 * n); } else { __int64 k = n / 2; return (rotation + (2 * k + 1) * power(3, k + 1)) / (2 * n); } } int main() { int n; while (cin >> n) { if (n == -1) { break; } if (n == 0) { cout << 0 << endl; } else { printf("%I64d/n", necklace(n)); } } return 0; } 

2012.04.04 刚发现Mr. Thursday写的一篇神文《圖解Pólya計數法》