本文介绍如何用C++实现一维离散傅里叶变换(Discrete Fourier Transform)。
1. 一维傅里叶变换公式简介
如果读者对傅里叶变换的认识处于一知半解的程度,那么建议先阅读相关文章,例如网络上广泛流传的《如果看了此文你还不懂傅里叶变换,那就过来掐死我吧》,以加深理解。
一维连续傅里叶变换的公式表达如下:

经过离散化后,上述公式变为:
其中M为x的个数,u=0,1,2,…,M-1。与连续形式的傅里叶变换相比,离散形式中e的指数多乘了一个1/M。
e -i2 πux/M可转化为三角函数cos(-2πux/M)+isin(-2πux/M),i为虚数单位。转化成三角函数形式,有利于计算机编程实现。故得到有利于编程实现的离散傅里叶变换公式如下:
观察上述离散傅里叶变换公式,不难发现,每计算一个F(u)的时间复杂度为O(N)(其中还可再细分为实数运算和复数运算,以及加法运算和乘法运算)。故算法的时间复杂度为O(N2)。对于超过50万个元素的向量,就目前的cpu运算速度而言,完成一次傅里叶变换所需要的时间是非常令人难以忍受的。而在图像处理中,一张高清图片的像素总数通常都会超过50万个。故有必要寻找一种可以快速计算傅里叶变换的算法。业界常用的快速算法叫FFT(基于蝶形分解的快速傅里叶变换)。后续将介绍如何用C++实现FFT。
对信号进行傅里叶变换,并在频域进行相关处理后,需要重建信号。这时候就需要进行离散傅里叶逆变换。离散傅里叶逆变换的公式如下:
我们将在代码中一并实现离散傅里叶逆变换。
2. 频域幅值的意义
很多刚接触傅里叶变换的人不了解频域图中的坐标和幅值的具体意义是什么。为了更好地理解傅里叶变换算法,这里有必要简短介绍一下频域图中的坐标和幅值的意义。
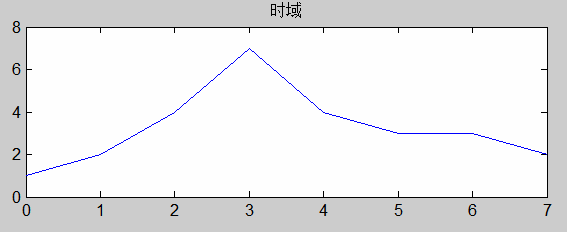
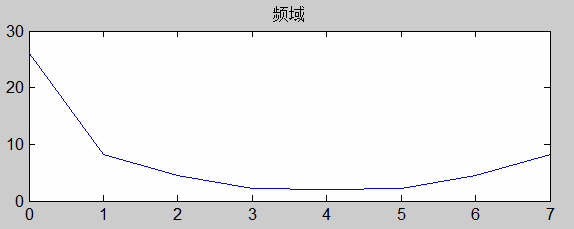
假设有一个一维信号为[1 2 4 7 4 3 3 2],在Matlab中对其进行傅里叶变换,得到求模后的变换结果为[26.0000 8.1922 4.4721 2.2107 2.0000 2.2107 4.4721 8.1922]。
通过Matlab分别作时域和频域的图形如下:
频域图上的横坐标共有8个点,从低到高分别对应8个频率。其中,频率为0的点对应的幅值为26,它是傅立叶变换的直流分量,是一维信号向量所有信号值的总和。频率为1的点的幅值,则等于以下两者构成的复数的模:一维信号对实数轴余弦函数cos(-2πx*1/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程度(数值上表现为计算相关);一维信号对复数轴余弦函数sin(-2πx*1/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程度(数值上表现为计算相关)。频率为2的点的幅值,则等于以下两者构成的复数的模:一维信号对实数轴余弦函数cos(-2πx*2/M)在定义域x∈0,1,2,3,...,M-1上的波形的符合程








 本文介绍了如何使用C++实现一维离散傅里叶变换(DFT),包括公式解析、算法时间复杂度分析以及C++代码实现。通过实例展示了DFT的计算过程,并与Matlab结果进行了对比验证。此外,还探讨了DFT在大数量级信号处理时的效率问题,为后续的快速傅里叶变换(FFT)做了铺垫。
本文介绍了如何使用C++实现一维离散傅里叶变换(DFT),包括公式解析、算法时间复杂度分析以及C++代码实现。通过实例展示了DFT的计算过程,并与Matlab结果进行了对比验证。此外,还探讨了DFT在大数量级信号处理时的效率问题,为后续的快速傅里叶变换(FFT)做了铺垫。

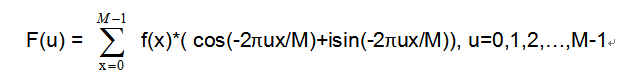
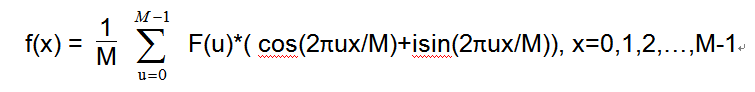
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








