POJ2553 The Bottom of a Graph(强连通量Tarjan算法)

为尊重原创，本博客是学习：https://blog.csdn.net/mengxiang000000/article/details/51672725，然后加上自己的再度理解，只是代码的搬运工，如果有侵权可联系。
原题链接：http://poj.org/problem?id=2553
The Bottom of a Graph
Time Limit: 3000MS Memory Limit: 65536K
Total Submissions: 12754 Accepted: 5243
Description
We will use the following (standard) definitions from graph theory. Let V be a nonempty and finite set, its elements being called vertices (or nodes). Let E be a subset of the Cartesian product V×V, its elements being called edges. Then G=(V,E) is called a directed graph.
Let n be a positive integer, and let p=(e1,…,en) be a sequence of length n of edges ei∈E such that ei=(vi,vi+1) for a sequence of vertices (v1,…,vn+1). Then p is called a path from vertex v1 to vertex vn+1 in G and we say that vn+1 is reachable from v1, writing (v1→vn+1).
Here are some new definitions. A node v in a graph G=(V,E) is called a sink, if for every node w in G that is reachable from v, v is also reachable from w. The bottom of a graph is the subset of all nodes that are sinks, i.e., bottom(G)={v∈V|∀w∈V:(v→w)⇒(w→v)}. You have to calculate the bottom of certain graphs.
Input
The input contains several test cases, each of which corresponds to a directed graph G. Each test case starts with an integer number v, denoting the number of vertices of G=(V,E), where the vertices will be identified by the integer numbers in the set V={1,…,v}. You may assume that 1<=v<=5000. That is followed by a non-negative integer e and, thereafter, e pairs of vertex identifiers v1,w1,…,ve,we with the meaning that (vi,wi)∈E. There are no edges other than specified by these pairs. The last test case is followed by a zero.
Output
For each test case output the bottom of the specified graph on a single line. To this end, print the numbers of all nodes that are sinks in sorted order separated by a single space character. If the bottom is empty, print an empty line.
Sample Input
3 3
1 3 2 3 3 1
2 1
1 2
0
Sample Output
1 3
2
Source
Ulm Local 2003

题解：说实话，这道题不翻译，几乎看不懂，只看得懂图的定义，输入输出，但是真正的题意一点都不懂，最重要还是这句话：A node v in a graph G=(V,E) is called a sink, if for every node w in G that is reachable from v, v is also reachable from w.网上说法是叫你求出度为0的强连通分量的元素。。。。

那么就开始：关于强连通量的题目，有这么一个算法：Tarjan，（如果不懂可以先看这个帖子：https://blog.csdn.net/mengxiang000000/article/details/51672725）
相信你看完之后，对于强连通等的定义以及tarjan有一定的理解了。

Tarjin是利用了dfs，至于为什么用dfs，在这里凭我对dfs的个人理解总结的：
1.利用dfs的递归性质，在连通图中（存在环），如果当前节点u想要访问的节点v在访问过的栈中，即是从这个在栈中的节点v可以访问到u（即v深搜到u），当前节点u又有边指向v，那么u可以到达v，v又可以到达u，就出现了环（如图0->1,1->0），这样就是一个连通分量。

2.利用dfs回溯的性质，当每一个节点相邻的所有节点访问完之后，在Tarjan算法中需要维护low，low用来存储这个连通分量的根（也就是起始节点），那么这个根是什么，也就是整个连通分量中访问顺序最小的，所以有low[u]=min(low[u],low[v])，假设u是上面1.中的当前节点u，v是上面1.中的节点v，如果遇到环，那么v就是这个环的根，也就是访问顺序最小的，那么我们就把low[u]赋值为low[v]，回溯的重点来了，当这个节点访问完了，开始回溯，然后又继续执行low[u]=min(low[u],low[v])操作，那么通过dfs的回溯的话，就可以把这个连通分量的low[]都变为根的low[]（也就是遇到环的时候的low）。

这里还是借用一下上面博客写的非常好的一个过程：
①首先进入0号节点，初始化其low【0】=dfn【0】=1，然后深搜到节点2，初始化其：low【2】=dfn【2】=2，然后深搜到节点1，初始化其：low【1】=dfn【1】=3；

②然后从节点1开始继续深搜，发现0号节点已经搜过了，没有继续能够搜的点了，开始回溯维护其值。low【1】=min（low【1】，low【0】）=1；low【2】=min（low【2】，low【1】）=1；low【0】=min（low【0】，low【2】）=1；

③这个时候猛然发现，low【0】==dfn【0】，这个时候不要太开心，就断定一定0号节点是一个关键点，别忘了，这个时候还有3号节点没有遍历，我们只有在其能够到达的节点全部判断完之后，才能够下结论，所以我们继续Dfs。

④继续深搜到3号节点，初始化其low【3】=dfn【3】=4，然后深搜到4号节点，初始化其：low【4】=dfn【4】=5，这个时候发现深搜到底，回溯，因为节点4没有能够到达的点，所以low【4】也就没有幸进行维护即：low【4】=dfn【4】（这个点一定是强连通分量的关键点，但是我们先忽略这个点，这个点没有代表性，一会分析关键点的问题），然后回溯到3号节点，low【3】=min（low【3】，low【4】）=4；发现low【3】==dfn【3】那么这个点也是个关键点，我们同样忽略掉。

⑤最终回溯到节点0，进行最后一次值的维护：low【0】=min（low【0】，low【3】）=0，这个时候我们猛然发现其dfn【0】==low【0】，根据刚才所述，那么这个点就是一个关键点：能够遍历其属强连通分量的点的起始点，而且没有其他点属于其他强连通分量能够有一条有向路径连到这个节点来的节点。

这里我就再介绍一下Tarjan算法： dfn[]用来标记当前及诶单再深搜过程中是第几个遍历到的点；
Low[]用来存储这个连通图中的跟，也就是最小子树的根；
定义low[u]=min(low[u],low[v]),u代表当前节点，v代表u能到达的节点；
这个数组再刚刚到达当前节点u的时候，初始化为low[u]=dfn[u]； 然后在进行下一次深搜之后回溯回来的时候，维护low[u]；
如果low[u]=dfn[u]，这就是一个关键点，从这个节点能够到达其强连通分量中的其他节点，但没有其他属于这个强连通以外的点能够到达这个节点。

核心代码：

void tarjan(int u){
	vis[u]=1;
	low[u]=dfn[u]=cnt++;//初始化  
	for(int i=0;i<mp[u].size();i++){//遍历u的所有相邻节点 
		int v=mp[u][i];
		if(vis[v]==0)
			tarjan(v);
		if(vis[v]==1)//出现了环，开始维护 
			low[u]=min(low[u],low[v]);
	}
	if(dfn[u]==low[u]){//当回溯到根节点，处理连通分量 
		sig++;
	}
}

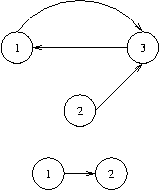
上面扯完Tarjan了，但是对这道题有什么作用呢，我们可以找出有多少个连通分量了，但是我们还没区分连通分量，所以我们还需要区分连通分量。这里用的是染色缩点法，通过染色缩点就可以把连通分量变为这样子（如图）：

核心代码（染色缩点）：

void tarjan(int u){
	vis[u]=1;
	low[u]=dfn[u]=cnt++;//初始化 
	stack[++tt]=u;//入栈方便找出整个连通分量 
	for(int i=0;i<mp[u].size();i++){//遍历u的所有相邻节点 
		int v=mp[u][i];
		if(vis[v]==0)
			tarjan(v);
		if(vis[v]==1)//出现了环，开始维护 
			low[u]=min(low[u],low[v]);
	}
	if(dfn[u]==low[u]){//当回溯到根节点，处理连通分量 
		sig++;
		do{
			color[stack[tt]]=sig;
			vis[stack[tt]]=-1;
		}while(stack[tt--]!=u);
	}
}

我们区分完连通分量了，我们最终需要找的是出度为0的连通分量，那么就看这个每个连通分量的所有节点有没有出度不是属于当前连通分量的，如果有节点的出度不属于当前连通分量，那么就出度加一。
核心代码：

for(int i=1;i<=n;i++){//在一个连通分量中查找有没有节点连上另外一个连通分量的节点 
		for(int j=0;j<mp[i].size();j++){
			int v=mp[i][j];
			if(color[i]!=color[v]){//如果连上了其他连通分量的节点 
				degree[color[i]]++;//出度加一 
			}
		}
	}
	int tot=0;
	for(int i=1;i<=sig;i++){
		if(degree[i]>0)//出度大于0的连通分量不管 
			continue;
		for(int j=1;j<=n;j++){
			if(i==color[j]){//遍历所有节点，如果节点的颜色和第i个连通分量颜色相同，ans存储下来 
				ans[tot++]=j;
			}
		}
	}

AC代码（POJ2553）：

#include<iostream>
#include<vector> 
#include<algorithm>
#include<string.h>
#include<cmath>
#define maxn 5010
using namespace std;
int dfn[maxn];
int low[maxn];
int stack[maxn];
int color[maxn];
int degree[maxn];
int vis[maxn];
int ans[maxn];
vector<int> mp[maxn];
int n,m,cnt,tt,sig;
void init(){
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	memset(stack,0,sizeof(stack));
	memset(degree,0,sizeof(degree));
	memset(color,0,sizeof(color));
	memset(ans,0,sizeof(ans));
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=n;i++)
		mp[i].clear();
}
void tarjan(int u){
	vis[u]=1;
	low[u]=dfn[u]=cnt++;//初始化 
	stack[++tt]=u;//入栈方便找出整个连通分量 
	for(int i=0;i<mp[u].size();i++){//遍历u的所有相邻节点 
		int v=mp[u][i];
		if(vis[v]==0)
			tarjan(v);
		if(vis[v]==1)//出现了环，开始维护 
			low[u]=min(low[u],low[v]);
	}
	if(dfn[u]==low[u]){//当回溯到根节点，处理连通分量 
		sig++;
		do{
			color[stack[tt]]=sig;
			vis[stack[tt]]=-1;
		}while(stack[tt--]!=u);
	}
}
void slove(){
	cnt=1;
	tt=-1;
	sig=0;
	for(int i=1;i<=n;i++){
		if(vis[i]==0)
			tarjan(i);
	}
	for(int i=1;i<=n;i++){//在一个连通分量中查找有没有节点连上另外一个连通分量的节点 
		for(int j=0;j<mp[i].size();j++){
			int v=mp[i][j];
			if(color[i]!=color[v]){//如果连上了其他连通分量的节点 
				degree[color[i]]++;//出度加一 
			}
		}
	}
	int tot=0;
	for(int i=1;i<=sig;i++){
		if(degree[i]>0)//出度大于0的连通分量不管 
			continue;
		for(int j=1;j<=n;j++){
			if(i==color[j]){//遍历所有节点，如果节点的颜色和第i个连通分量颜色相同，ans存储下来 
				ans[tot++]=j;
			}
		}
	}
	sort(ans,ans+tot);//从小到大输出 
	for(int i=0;i<tot;i++){
		if(i==0)
			cout<<ans[i];
		else
			cout<<" "<<ans[i];
	}
	cout<<endl;
}
int main(){
	while(cin>>n){
		if(n==0)
			break;
		cin>>m;
		init();
		int x,y;
		for(int i=0;i<m;i++){
			cin>>x>>y;
			mp[x].push_back(y);
		}
		slove();
	}
	return 0;
}