DSAA Homework 2

Exercises

3.4

a

by the definition
$3*2^{n'}=64*3*2^n$
$2^{n'}=2^{n+6}$
n’=n+6

c

by the definition

$8n'=64*8n$
$n'=64n$

---

3.8

c

For the all values of n > 1, $c_4nlogn + c_5n \le c_4nlogn + c_5nlogn \le (c_4+c_5)nlogn$. Therefore, by the definition, T(n) is in O(n) for $n_0 = 1$ and $c = c_4 + c_5$
For all n > 1, $c_4nlogn + c_5n \ge c_4n + c_5n \ge (c_4 + c_5)n$. Therefore, by the definition, T(n) is in $\Omega(n)$ for $n_0 = 1$ and $c = c_4 + c_5$.

d

For the all values of n > 29, $c_62^n + c_7n^6 \le (c_6 + c_7)2^n$. Therefore, by the definition, T(n) is in O(n) for $n_0 = 29$ and $c = c_4 + c_5$.
For the all values of n > 29, $c_62^n + c_7n^6 \ge (c_6 + c_7)n^6$. Therefore, by the definition, T(n) is in $\Omega(n)$ for $n_0 = 29$ and $c = c_4 + c_5$.

---

3.11

b

$\lim\limits_{n\to\infty} \frac{\sqrt{n}}{logn^2} = \lim\limits_{n\to\infty} \frac{\sqrt{n}}4 = \infty$ , so f(n) is in $\Omega(g(n))$

e

$\lim\limits_{n\to\infty} \frac{nlogn + n}{logn} = \lim\limits_{n\to\infty} n = \infty$ , so f(n) is in $\Omega(g(n))$

h

$\lim\limits_{n\to\infty} \frac{2^n}{10n^2} = \infty$ , so f(n) is in $\Omega(g(n))$

---

3.12

a

$\Theta(1)$

b

$\Theta(n)$

c

$\Theta(n^2)$

d

$\Theta(n^2)$

e

$\Theta(nlogn)$

f

$\Theta(nlogn)$

g

$\Theta(n^2logn)$

---

Projects

3.2

#include<cstdio>
#include<cstdlib>
#include<ctime>
const int maxn = 1e7 + 100;
int a[maxn];
int random(int n){
    return rand() % n;
}
int SeSearch(int val, int n){
    for(int i = 0; i < n; i++)
        if(a[i] == val) return i;
    return -1;
}
int BiSearch(int val, int n){
    int l = 0, r = n;
    while(r - l > 1){
        int m = (l + r) / 2;
        if(a[m] > val) r = m;
        else l = m;
    }
    return a[l] == val ? l : -1;
}
int main(){
    for(int i = 0; i < maxn; i++) a[i] = i;
    const int T = 100000;
    int tmp;
    clock_t begin, end;
    for(int n = 10, k = 1; k <= 7; n *= 10, k++){
        printf("i:%d ", k);
        begin = clock();
        for(int i = 0; i < T; i++)
            tmp = SeSearch(random(n), n);
        end = clock();
        printf("%.2lf ", (double)(end - begin) / CLOCKS_PER_SEC);

        begin = clock();
        for(int i = 0; i < T; i++)
            tmp = BiSearch(random(n), n);
        end = clock();
        printf("%.2lf\n", (double)(end - begin) / CLOCKS_PER_SEC);
    }
    return 0;
}

i	Sequential	Binary
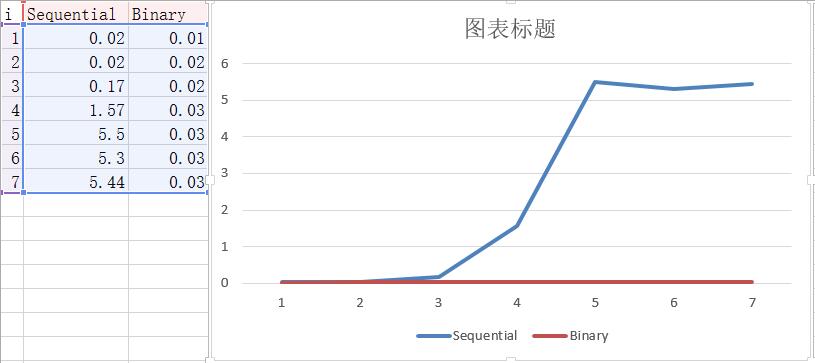
1	0.02	0.01
2	0.02	0.02
3	0.17	0.02
4	1.57	0.03
5	5.50	0.03
6	5.30	0.03
7	5.44	0.03

So binary search always faster than sequential search.