二维差分算法最细致解析

解析前提：大家比较明白了一维差分算法和前缀和算法

大家要注意一些编程思维：

首先编程基本运算就是迭代，迭代思维是不考虑边界问题，更重要的是将计算的问题一般化，抽象化，在过程中考虑变量身份。其次就是互逆思维，就比如我们今天讲的前缀和与差分算法，就是一对矛盾，这两个相辅相成，有前缀和矩阵必然存在差分矩阵，两者不能单独分开讨论！

1、差分算法最本质作用是通过差分矩阵随意实现前缀和子矩阵整体数值的增加和减少；

2、差分运算和前缀和运算互为逆运算；

我们假设存在差分矩阵Bn和前缀和矩阵An,则存在一下关系：

  

 从图中我们可以很清晰发现aij 就是b矩阵中bij往左往上所有元素（包括bij所在行所在列）的值的总合，显然往右进行的是前缀和，那么我们怎么用数学表达式表示呢？

 做一个简单示意图：

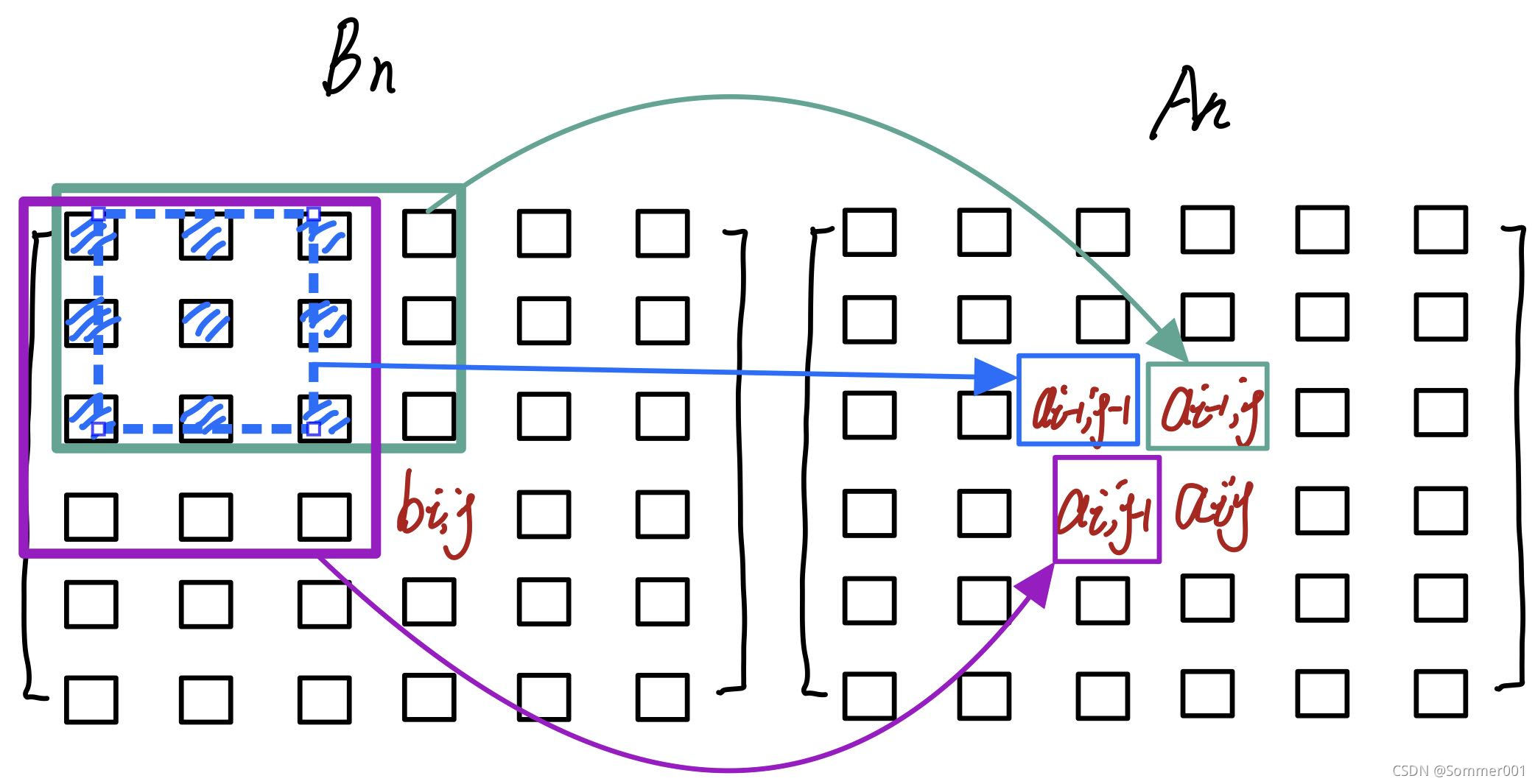
 上图表示了一般情况，那么我们可以得到下面的等式：

//对应代码为：
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];

 这个等式就将前缀和矩阵和差分矩阵联系在一起，同时体现了迭代思维，由aij之前的值求自身，然后自身又作为已知的值求下一个值，这样我们通过已知差分矩阵Bn得到前缀和矩阵An&#x