LBP特征详细原理-python代码复现

LBP特征提取算法

LBP(Local Binary Patterns，局部二值模式)是提取局部特征作为判别依据的，一种有效的纹理描述算子，度量和提取图像局部的纹理信息，它具有旋转不变性和灰度不变性等显著的优点，对光照具有不变性。而且，提取的特征是图像的局部的纹理特征。原始的LBP于1994年提出，它反映内容是每个像素与周围像素的关系。后被不断的改进和优化，分别提出了LBP旋转不变模式、LBP均匀模式等。
灰度不变性：指的是光照变化是否会对描述产生影响。以上面的8邻域来说，光照变化很难改变中心像素点的灰度值与周围8个像素的大小关系。因为光照是一种区域性质的变化，而不是单像素性质的变化。

1、LBP特征描述

LBP的基本思想是定义于像素的8邻域中(3x3的窗口), 以中心像素的灰度值为阈值, 将周围8 个像素的值与其比较, 如果周围的像素值小于中心像素的灰度值, 该像素位置就被标记为0, 否则标记为1。这样3x3的邻域内的八个点经过比较能够产生8位二进制数(通常转换为十进制，即LBP码，共256种)，每个像素得到一个二进制组合, 即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。

（01111100）=4+8+16+32+64=124


一般以左上角为第一个点，逆时针进行旋转

(原论文的公式定义）
一个更加正式的LBP操作可以被定义为：

其中（Xc, yc) 是中心像素，亮度是ic ；而 ip则是相邻像素的亮度。s是一个符号函数：

2、LBP的改进版本：

(1)圆形LBP算子

基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺寸的纹理特征，达到灰度和旋转不变性的要求。将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子。

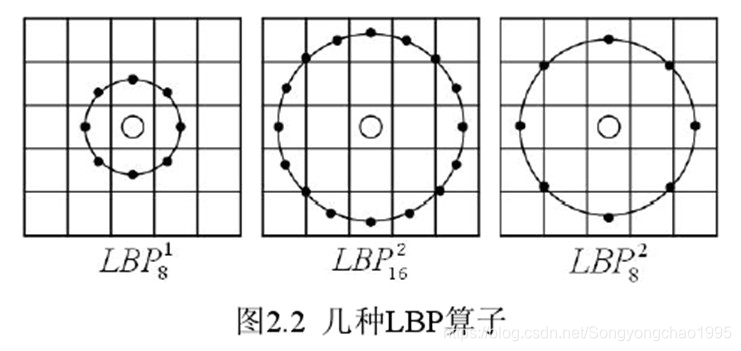
(2)LBP旋转不变模式
原始的LBP不具有旋转不变性，图像的旋转就会得到不同的LBP值。这样我们就提出了旋转不变的LBP模式。旋转不变的LBP计算公式如下：

Maenpaa等人又将 LBP算子进行了扩展，提出了具有旋转不变性的 LBP 算子，即不断旋转圆形邻域得到一系列初始定义的 LBP值