【C++进阶】二叉搜索树的介绍、模拟实现和相关习题-CSDN博客

本文链接：https://blog.csdn.net/Stark_Skywalker/article/details/140619393

1. 概念

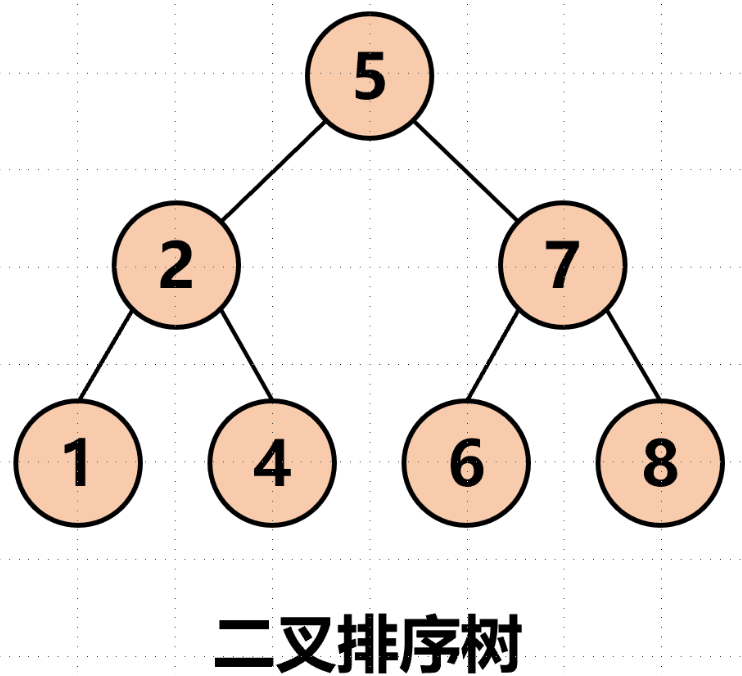
二叉搜索树又叫二叉排序树、二叉查找树。可以为空，也可以不为空，具体有以下的特性：(二叉搜索树没有重复的值)

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

做题笔记

对其中序遍历时，输出结果是有序序列。
给定一棵二叉搜索树的前序和中序遍率历结果，无法确定这棵二叉搜索树

在二叉搜索树中进行中序遍历时，每个节点只会被访问一次，因此遍历的时间复杂度为 $O (N)$ 。这个复杂度表示无论树的结构如何（只要有 N 个节点），遍历树的时间是与节点数成线性关系的。
但是给定一棵二叉树并不能在线性时间复杂度内转化为平衡二叉搜索树，因为涉及旋转等操作，时间复杂度不是线性的。

2. 操作及模拟实现

2.1 二叉搜索树的查找

a. 从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
b. 最多查找高度次，走到到空，还没找到，这个值不存在。

非递归实现

bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
			//当前结点的值比要查找的值还小
			//说明key可能在右子树
		{
			cur = cur->_right;
		}
		else if (cur->_key > key)
			//当前结点的值比要查找的值还大
			说明key可能在左子树
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
	//经过以上查找仍然找不到。
	return false;
}

递归实现

bool _FindR(Node* root, const K& key)
{
	if (root == nullptr)
	{
		return false;
	}

	if (root->_key < key)
	{
		return _FindR(root->_left, key);
	}
	else if (root->_key > key)
	{
		return _FindR(root->_right, key);
	}
	else
	{
		return true;
	}
}

2.2 二叉搜索树的插入

插入的具体过程如下：
a. 树为空，则直接新增节点，赋值给root指针
b. 树不空，按二叉搜索树性质查找插入位置，插入新节点

非递归实现

bool Insert(const K& key)
{
	if (_root == nullptr)
	{
		_root = new Node(key);//直接构造一个新结点。
		return true;
	}
	
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)//找到结点要插入的位置
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else//相等的情况
		{
			return false;
		}
	}

	cur = new Node(key);
	if (parent->_key < key)
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}
	return true;
}

找到插入位置，还知道父节点才能往后插入，所以咱们需要一个 parent 结点指针。（双指针那种感觉）

递归实现

bool _InsertR(Node* root, const K& key)
{
	if (root == nullptr)
	{
		root = new Node(key);
		return true;
	}
//以下是寻找过程，只达到上面if的位置。
	if (root->_key < key)
	{
		return _InsertR(root->_right, key);
	}
	else if (root->_key > key)
	{
		return _InsertR(root->_left, key);
	}
	else//找到相等
	{
		return false;
	}
}

2.3 中序遍历

void InOrder()
{
	_InOrder(_root);
	cout << endl;
}

//类似于封装
void _InOrder(Node* root)
{
	if (root == nullptr)
		return;

	_InOrder(root->_left);
	cout << root->_key << " ";
	_InOrder(root->_right);
}

2.4 删除

情况类型分析：

没有孩子
一个孩子
两个孩子
前两个又可以归为一类。

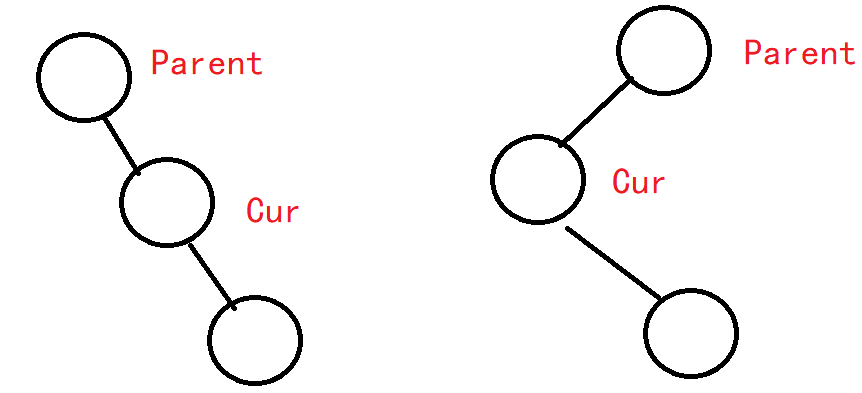
image.png|500
只有一个孩子且没有左子树

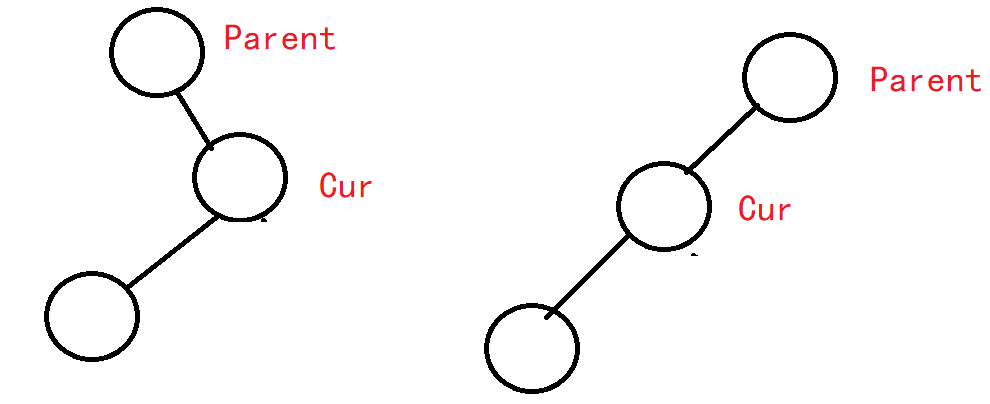
只有一个孩子且没有右子树

有两个子树——替换法删除
找一个能替换的结点，交换值，转换删除它。
这个结点可以是：

左子树的最大结点——左子树最右结点
右子树的最小结点——右子树最左结点（这段代码采取的是这个）
非递归实现

bool Erase(const K& key)
{
	if (_root == nullptr)
		return false;
	else
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else//相等的情况,找到了！
			{
				//接下来的两个if-else都是讨论只有一个子树的情况
				//也包括了没有左右子树的情况
				if (cur->_left == nullptr)//没有左子树
				{
					if (cur == _root)//删除的结点为顶点
					{
						_root = cur->_right;
					}
					else
					{
						//在删除之前，将cur结点的上一个结点（即父节点）的指向进行更改
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
						delete cur;
						return true;
					}
				}
				//相对上一段if只改动了parent指向——cur的左结点
				else if (cur->_right == nullptr)
				{
					if (cur == _root)//删除的结点为顶点
					{
						_root = cur->_right;
					}
					else
					{
						//在删除之前，将cur结点的上一个结点（即父节点）的指向进行更改
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
						delete cur;
						return true;
					}
				}
				else//左右都有子树，此时cur和parent都就位
				{
					//替换法
					Node* rightMinParent = cur;
					Node* rightMin = cur->_right;

					//找到右子树最左结点
					while (rightMin->_left)
					{
						rightMinParent = rightMin;
						rightMin = rightMin->_left;
					}
					//找到了，并该值覆盖要删除的值。
					cur->_key = rightMin->_key;

					//判断删除的结点是上一个结点的哪一侧，
					// 并将该删除结点以下最大值的结点，移到该删除结点位置。
					//这也是有rightMinparent的原因，在删除rightMin之前需要重新指向。
					if (rightMin == rightMinParent->_left)
					{
						rightMinParent->_left = rightMin->_right;
					}
					else
					{
						rightMinParent->_right = rightMin->_right;
					}
					delete rightMin;
					return true;
				}
			}
		}
	}
	return false;
}

递归实现

bool _EraseR(Node* root, const K& key)
{
	if (root == nullptr)
	{
		return false;
	}


	if (root->_key < key)
	{
		return EraseR(root->_left, key);
	}
	else if (root->_key > key)
	{
		return EraseR(root->_right, key);
	}
	else
		//此时root结点是我们要删除的结点
	{
		Node* del = root;
		//指定删除的结点没有子树或者有一棵子树的情况
		if (root->_right == nullptr)
		{
			root = root->_left;
		}
		else if (root->_left == nullptr)
		{
			root = root->_right;
		}
		else
		{
			Node* rightMin = root->_right;
			while (rightMin->_left)
			{
				rightMin = rightMin->_left;
			}
			swap(root->_key, rightMin->_key);
			return _EraseR(root->_right, key);
			//交换完值后，把rightMin位置的结点删除
		}
	}
	delete del;
	return true;
}

注意：这里的引用，既是父节点的指针的别名，也是子结点的地址
也就可以做到 root = root -> left
为什么可以这么做？
引用的底层还是使用指针实现的，引用在语法上的定义就是变量的别名，所以把 root->_right 传递进去之后，下一个函数栈的 root 和当前函数栈的 root->_right 是相同的，所以下一个函数栈中对 root 的操作就是操作当前函数栈的 root->_right

2.5 构造及析构

拷贝构造

BSTree(const BSTree<K>& t)
{
	_root = Copy(t._root);
}

Node* Copy(Node* root)
{
	if (root == nullptr)
	{
		return nullptr;
	}

	Node* newRoot = new Node(root->_key);
	
}

赋值构造

BSTree<K>& operator= (BSTree<K> t)
{
	swap(_root, t._root);
	return *this;
}

析构

~BSTree()
{
	Destroy(_root);
}

//注：这个是写在private里的
void Destroy(Node* root)//也是采用递归 后序遍历删除结点
{
	if (root == nullptr)
		return;

	Destroy(root->_left);
	Destroy(root->_right);
	delete root;
}

采用后序遍历这种方式可以确保在删除当前节点之前，已经删除了它的所有子节点，从而避免内存泄漏和非法访问。——先删除子节点，再删除父节点。

应用

K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树，在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

void TestBSTree3()
{
	// 输入单词，查找单词对应的中文翻译
	BSTree<string, string> dict;
	dict.Insert("string", "字符串");
	dict.Insert("tree", "树");
	dict.Insert("left", "左边、剩余");
	dict.Insert("right", "右边");
	dict.Insert("sort", "排序");
	// 插入词库中所有单词
	string str;
	while (cin >> str)
	{
		BSTreeNode<string, string>* ret = dict.Find(str);
		if (ret == nullptr)
		{
			cout << "单词拼写错误，词库中没有这个单词:" << str << endl;
		}
		else
		{
			cout << str << "中文翻译:" << ret->_value << endl;
		}
	}
}

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方式在现实生活中非常常见：
比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对；再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是<word, count>就构成一种键值对。
K-V 模型源码实现

namespace key_value
{
	template<class K, class V>
	struct BSTreeNode
	{
		typedef BSTreeNode<K, V> Node;

		Node* _left;
		Node* _right;
		K _key;
		V _value;

		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			, _value(value)
		{}
	};

	template<class K, class V>
	class BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		bool Insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key, value);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(key, value);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

			return true;
		}

		Node* Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}

			return nullptr;
		}

		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_right)
							{
								parent->_right = cur->_right;
							}
							else
							{
								parent->_left = cur->_right;
							}
						}

						delete cur;
						return true;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							if (cur == parent->_right)
							{
								parent->_right = cur->_left;
							}
							else
							{
								parent->_left = cur->_left;
							}
						}

						delete cur;
						return true;
					}
					else
					{
						// 替换法
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}

						cur->_key = rightMin->_key;

						if (rightMin == rightMinParent->_left)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;

						delete rightMin;
						return true;
					}
				}
			}

			return false;
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}

	private:
		void _InOrder(Node* root)
		{
			if (root == nullptr)
				return;

			_InOrder(root->_left);
			cout << root->_key << ":" << root->_value << endl;
			_InOrder(root->_right);
		}

	private:
		Node* _root = nullptr;
	};
}

使用例子

int main()
{
	string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "西瓜", "香蕉", "草莓" };
	key_value::BSTree<string, int> t;
	for (auto& e : arr)
	{
		// 1、不在，说明水果第一次出现，则插入<水果, 1>
  		// 2、在，则查找到的节点中水果对应的次数++
		auto ret = t.Find(e);
		if (ret == nullptr)
		{
			// 第一次出现
			t.Insert(e, 1);
		}
		else
		{
			ret->_value++;
		}
	}

	t.InOrder();

	return 0;
}

性能分析

最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为： $log_2 N$
最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为： $\frac{N}{2}$

那能否进行改进，不论按照什么次序插入关键码，二叉搜索树的性能都能达到最优？
那就等到后面的 AVL 树和红黑树上场了。

常见题目

根据二叉树创建字符串

class Solution {
public:
    string tree2str(TreeNode* root) {
        if (root == nullptr)
        {
            return "";
        }

        //1、左右都为空，要省略括号
        //2、右为空，也省略括号

        //前序遍历
        string ret = to_string(root->val);

        //还有一个当左为空时依旧可以打印出括号
        if (root->left || root->right)
        {
            ret += "(";
            ret += tree2str(root->left);
            ret += ")";
        }

        if (root->right)
        {
            ret += "(";
            ret += tree2str(root->right);
            ret += ")";
        }

        return ret;
    }
};

二叉树的层序遍历

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv;
        queue<TreeNode*> q;//存放节点指针
        int levelSize = 0;

        if (root)
        {
            q.push(root);
            levelSize = 1;
        }

        while (!q.empty())
        {
            //一层出完，同时把下一层入队
            vector<int> v;
            while (levelSize--)
            {
                TreeNode* front = q.front();
                q.pop();

                v.push_back(front->val);

                if (front->left)//如果存在
                    q.push(front->left);

                if (front->right)//如果存在
                    q.push(front->right);
            }

            //当前层出完了后，剩下的就是下一层的所有节点入队列，队列size就是下一层数据个数
            levelSize = q.size();
            vv.push_back(v);
        }
        return vv;
    }
};

二叉树的最近公共祖先

最近公共祖先：一个孩子在左，一个孩子在右，那么该节点就是。
如果结点 A 在结点 B 的子树中，那么结点 B 就是最近的公共祖先。
方法一：

class Solution {
public:
	bool IsInTree(TreeNode* root, TreeNode* x)
	{
		if (root == nullptr)
		{
			return false;
		}
		return root == x || IsInTree(root->left, x) || IsInTree(root->right, x);
	}

	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		//先把两种简单情况列出来，一个为空，一个就是根节点

		if (root == NULL)
		{
			return NULL;
		}

		if (root == p || root == q)
		{
			return root;
		}

		//判断p和q结点在哪一棵子树下
		bool pInLeft, pInRight, qInLeft, qInRight;
		pInLeft = IsInTree(root->left, p);
		pInRight = !pInLeft;

		qInLeft = IsInTree(root->left, q);
		qInRight = !qInLeft;

		//一左一右、都在左、都在右
		if ((pInLeft && qInRight) || (pInRight && qInLeft))
		{
			return root;
		}
		else if (pInLeft && qInLeft)
		{
			return lowestCommonAncestor(root->left, p, q);
		}
		else if (pInRight && qInRight)
		{
			return lowestCommonAncestor(root->right, p, q);
		}

		assert(false);
		return NULL;
	}
};

方法二：
image.png|450

class Solution {
public:
    bool GetPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
    {
        if (root == nullptr)
        {
            return false;
        }

        path.push(root);
        if (root == x)
        {
            return true;
        }

        if (GetPath(root->left, x, path))
        {
            return true;
        }

        if (GetPath(root->right, x, path))
        {
            return true;
        }

        path.pop();
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> pPath, qPath;
        GetPath(root, p, pPath);
        GetPath(root, q, qPath);

        //两个路径找交点
        while (pPath.size() != qPath.size())
        {
            if (pPath.size() > qPath.size())
            {
                pPath.pop();
            }
            else
                qPath.pop();
        }

        while (pPath.top() != qPath.top())
        {
            pPath.pop();
            qPath.pop();
        }

        return pPath.top();
    }
};

二叉搜索树与双向链表

class Solution {
public:
    // pPrev标记刚刚转化的节点，pRoot表示现在要转化的二叉树，pRoot前一个处理的节点是pPrev
    void _Convert(TreeNode* pRoot, TreeNode*& pPrev)
    {
        // 空树：不用转化，直接返回
        if (nullptr == pRoot)
            return;

        // 将pRoot的左子树转化为双向链表
        _Convert(pRoot->left, pPrev);

        // pRoot的left指向其前一个处理的节点，即pPrev
        // pRoot的right域没有办法在本次递归中处理，因为下一个节点不知道
        // 在本次中只能处理当前节点的left
        pRoot->left = pPrev;

        // 前一个节点的right指针域没有处理，right指针域指向后一个节点，即pRoot
        if (pPrev)
            pPrev->right = pRoot;

        pPrev = pRoot;

        // 将pRoot的右子树转化为双向链表
        _Convert(pRoot->right, pPrev);
    }

    TreeNode* Convert(TreeNode* pRootOfTree)
    {
        if (nullptr == pRootOfTree)
            return nullptr;

        // 找双向链表的第一个节点，即树中最小的节点
        TreeNode* pHead = pRootOfTree;
        while (pHead->left)
            pHead = pHead->left;

        // 使用prev标记刚刚转化过的节点
        TreeNode* prev = nullptr;
        _Convert(pRootOfTree, prev);
        return pHead;
    }
};

从前序与中序遍历序列构造二叉树

前序确定根，中序确定左右区间——当前问题和分割子问题
区间不存在即为空树——确定返回条件

class Solution {
public:
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int  inbegin, int inend) {
        if (inbegin > inend)
            return nullptr;

        TreeNode* root = new TreeNode(preorder[prei++]);
        //因为这里是引用，走左树再走有树，已经加过了的。

        //分割中序左右区间
        int rooti = inbegin;
        while (rooti <= inend)
        {
            if (inorder[rooti] == root->val)
            {
                break;
            }
            else
                rooti++;
        }
        //[inbegin,rooti-1] rooti [rooti+1,inend]
        root->left = _buildTree(preorder, inorder, prei, inbegin, rooti - 1);
        root->right = _buildTree(preorder, inorder, prei, rooti + 1, inend);

        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int i = 0;
        TreeNode* root = _buildTree(preorder, inorder, i, 0, inorder.size() - 1);
        return root;
    }
};

从中序与后序遍历序列构造二叉树

/*
思路：
 1. 从后序遍历结果中获取到树的根节点，注意：后序遍历规则：左子树、右子树、根节点，因此应该从后往前获取根节点
 2. 在中序遍历结果中确定根节点的位置，按照该位置将中序遍历结果分为两部分
    右半部分是根节点的右子树，递归创建根节点的右子树---->注意先要还原根的右子树
    左半部分是根节点的左子树，递归创建根节点的左子树
*/

class Solution {
public:
    TreeNode* _buildTree(vector<int>& postorder, int& index, vector<int>& inorder, int begin, int end)
    {
        // index越界时，说明树中的节点已经创建完毕
        TreeNode* pRoot = nullptr;
        if (index < 0)
            return pRoot;

        // 还原根节点
        pRoot = new TreeNode(postorder[index]);

        // 在中序遍历结果中找根节点的位置，根节点左侧是是根的左子树，右侧的节点是根的右子树
        int mid = begin;
        while (mid < end)
        {
            if (inorder[mid] == postorder[index])
                break;

            mid++;
        }

        // 如果右子树存在，递归创建根节点的右子树
        if (mid + 1 < end)
        {
            pRoot->right = _buildTree(postorder, --index, inorder, mid + 1, end);
        }

        // 左子树存在，递归创建根节点左子树
        if (begin < mid)
        {
            pRoot->left = _buildTree(postorder, --index, inorder, begin, mid);
        }

        return pRoot;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
    {
        int index = postorder.size() - 1;
        return _buildTree(postorder, index, inorder, 0, inorder.size());
    }
};

二叉树的前序遍历

根节点及其左子树先解决，再处理右子树。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> s;
        vector<int> v;
        TreeNode* cur = root;

        while (cur || !s.empty())
        {
            //1.访问左路结点，左路结点入栈
            while (cur)
            {
                v.push_back(cur->val);
                s.push(cur);
                cur = cur->left;
            }

            //2.依次访问左路节点的子树
            TreeNode* top = s.top();
            s.pop();

            //3.访问左路节点的右子树
            cur = top->right;
        }
        return v;
    }
};

二叉树的中序遍历

class Solution {
public:
	vector<int> inorderTraversal(TreeNode* root) {
		stack<TreeNode*> s;
		vector<int> v;
		TreeNode* cur = root;

		while (cur || !s.empty())
		{
			//1.访问左路结点，左路结点入栈
			while (cur)
			{
				s.push(cur);
				cur = cur->left;
			}

			//2.依次访问左路节点的子树
			TreeNode* top = s.top();
			s.pop();

			//从栈里面取出这个结点时，一定是它的左子树访问完了。
			v.push_back(top->val);

			//3.访问左路节点的右子树
			cur = top->right;
		}
		return v;
	}
};

二叉树的后序遍历

class Solution {
public:
	vector<int> postorderTraversal(TreeNode* root) {
		stack<TreeNode*> s;
		vector<int> v;
		TreeNode* cur = root;
		TreeNode* prev = nullptr;

		while (cur || !s.empty())
		{
			//1.访问左路结点，左路结点入栈
			while (cur)
			{
				s.push(cur);
				cur = cur->left;
			}

			//2.依次访问左路节点的子树
			TreeNode* top = s.top();
			// 栈里面取到top代表top的左子树已经访问完了
			//1、当前结点右子树为空，则访问当前节点
			//或者右子树不为空，但是上一个访问节点是右子树的根，代表右子树访问过了，可以访问
			//2、否则右子树不为空，子问题访问右子树
			if (top->right == nullptr || top->right == prev)
			{
				v.push_back(top->val);
				s.pop();

				prev = top;
			}
			else
			{
				cur = top->right;
			}
		}
		return v;
	}
};