Arc of Dream

Arc of Dream

Time Limit: 2000/2000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 7124    Accepted Submission(s): 2232

 

Problem Description

An Arc of Dream is a curve defined by following function:

where
a0 = A0
ai = ai-1*AX+AY
b0 = B0
bi = bi-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?

 

 

Input

There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 1018, and all the other integers are no more than 2×109.

 

 

Output

For each test case, output AoD(N) modulo 1,000,000,007.

 

Sample Input

1

1 2 3

4 5 6

2

1 2 3

4 5 6

3

1 2 3

4 5 6

 

Sample Output

4

134

1902

思路：

 

 

 

 

 

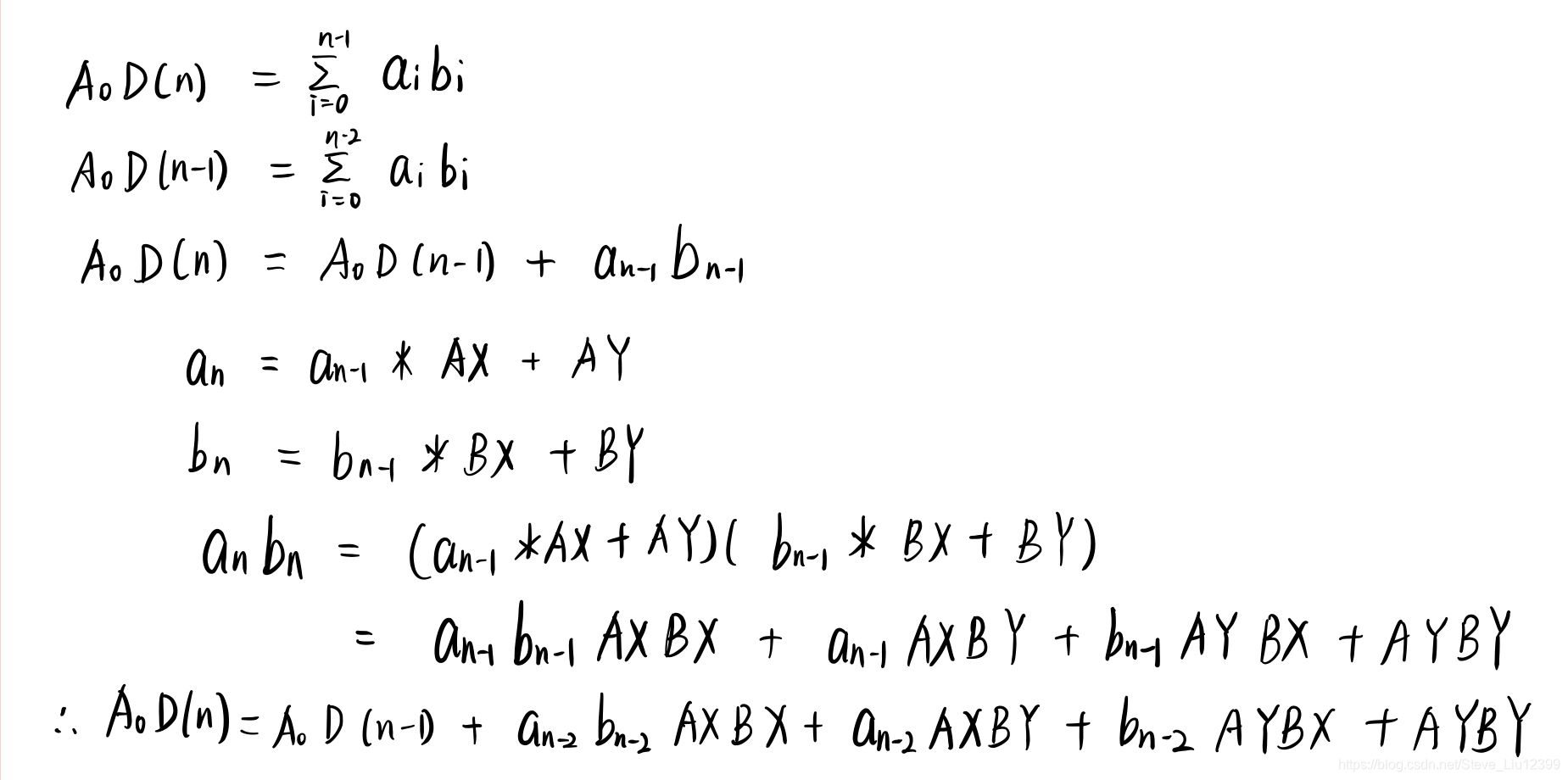
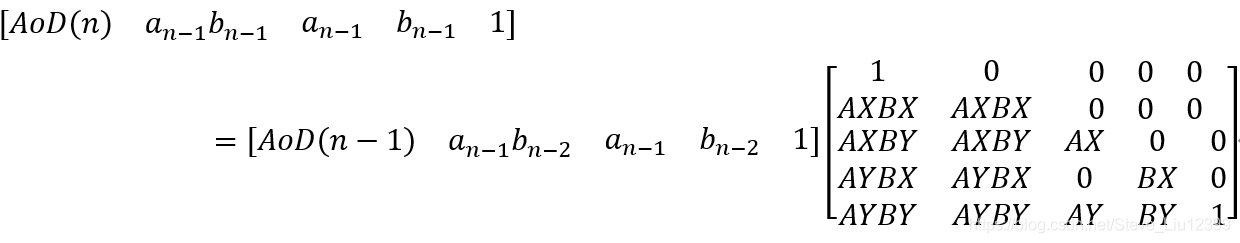
以下是ac代码：(由于A0,AX,AY,B0,BX,BY数据比较大，所以要取余，另外当n =0的时候，输出0)

#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;

typedef long long ll;
const ll mod = 1e9 + 7;

struct matrix{
    ll x[10][10];
    ll n, m;
    matrix(){memset(x, 0, sizeof(x));}
};

matrix multiply(matrix &a, matrix &b)
{
    matrix c;
    c.n = a.n;
    c.m = b.m;
    for(int i = 1; i <= a.n; i++){
        for(int j = 1; j <= b.m; j++){
            c.x[i][j] = 0;
            for(int k = 1; k <= b.m; k++){
//                c.x[i][j] = c.x[i][j] +  (a.x[i][k] % mod) * (b.x[k][j] % mod) % mod;
                c.x[i][j] += a.x[i][k] * b.x[k][j] % mod;
            }
            c.x[i][j] %= mod;
        }
    }
    return c;
}

ll AX, AY, BX, BY;

matrix mpow(matrix &a, ll n)
{
    matrix res;
    res = a;
    matrix change;
    change.n = change.m = 5;
    for(int i = 1; i <= 5; i++){
        for(int j = 1; j <= 5; j++)
            change.x[i][j] = 0ll;
    }
    change.x[1][1] = change.x[5][5] = 1;
    change.x[2][1] = change.x[2][2] = (AX % mod * BX % mod) % mod;
    change.x[3][1] = change.x[3][2] = (AX % mod * BY % mod) % mod;
    change.x[4][1] = change.x[4][2] = (AY % mod * BX % mod) % mod;
    change.x[5][1] = change.x[5][2] = (AY % mod * BY % mod) % mod;
    change.x[3][3] = AX % mod;
    change.x[4][4] = BX % mod;
    change.x[5][3] = AY % mod;
    change.x[5][4] = BY % mod;
    while(n > 0){
        if(n & 1)res = multiply(res, change);
        change = multiply(change, change);
        n >>= 1;
    }
    return res;
}

int main()
{
    ll A0, B0;
    ll n;
    while(~scanf("%lld%lld%lld%lld%lld%lld%lld", &n, &A0, &AX, &AY, &B0, &BX, &BY)){
        if(n == 0){
            cout<<"0"<<endl;
            continue;
        }
        A0 %= mod;
        AX %= mod;
        AY %= mod;
        B0 %= mod;
        BX %= mod;
        BY %= mod;
        matrix m;
        m.n = 1;
        m.m = 5;
        m.x[1][1] = (A0 % mod)* (B0 % mod) % mod;
        m.x[1][2] = (A0 % mod)* (B0 % mod) % mod;
//        m.x[1][2] = A0*B0;
        m.x[1][3] = A0 % mod;
        m.x[1][4] = B0 % mod;
        m.x[1][5] = 1;
        m = mpow(m, n-1);
        printf("%lld\n", m.x[1][1] % mod);
    }
    return 0;
}