树状数组

 

目录

定义

结构起源

分析

 常用操作

更新元素

求前缀和

实战

---

定义

       树状数组(Binary Indexed Tree(BIT), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值。

       现多用于高效计算数列的前缀和， 区间和。

结构起源

       正如所有的整数都可以表示成2的幂和，我们也可以把一串序列表示成一系列子序列的和。采用这个想法，我们可将一个前缀和划分成多个子序列的和，而划分的方法与数的2的幂和具有极其相似的方式。一方面，子序列的个数是其二进制表示中1的个数，另一方面，子序列代表的f[i]的个数也是2的幂。

分析

如何将普通数组转变为树状数组呢？（看下图）

 

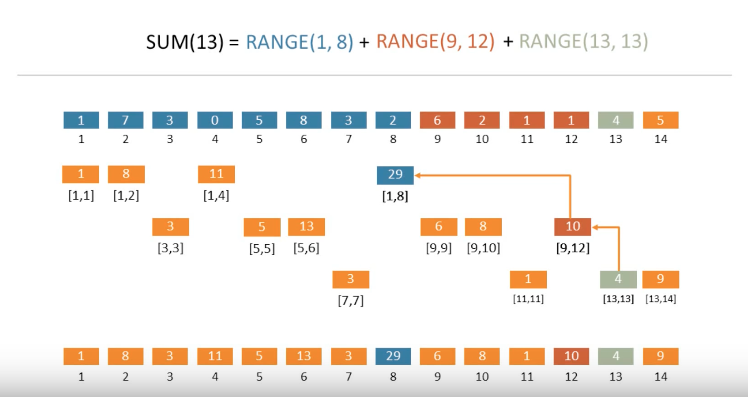
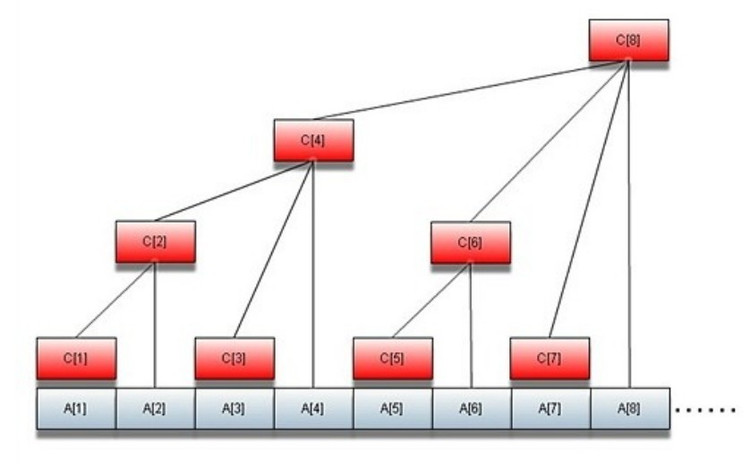
（最上面一行为 A 数组，为原始数组；最下面一行为 C 数组，为树状数组）

令这棵树的结点编号为C1，C2...Cn。令每个结点的值为这棵树的值的总和，那么容易发现：

（0001）C1 = A1

（0010）C2 = A1 + A2

（0011）C3 = A3

（0100）C4 =  A1 + A2 + A3 + A4

（0101）C5 = A5

（0110）C6 = A5 + A6

（0111）C7 = A7

（1000）C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

这里有一个有趣的性质：

设节点编号为x，那么这个节点管辖的区间为2^k（其中k为x二进制末尾0的个数）个元素。因为这个区间最后一个元素必然为Ax，

所以很明显：Cn = A(n – 2^k + 1) + A(n - 2^k + 2) ... + An

 算这个2^k有一个快捷的办法，定义一个函数如下即可：

• 定义一个Lowbit函数，返回参数转为二进制后,最后一个1的位置所代表的数值.

例如，Lowbit(34) 的返回值将是2；而 Lowbit(12) 返回4；Lowbit(8) 返回8。

34 = 32+2：0010 0100  最后一个 1（从低位往前数所遇到的第一个 1）是 2^1 位上的 1，故 Lowbit(34) = 2^1 = 2；

12 = 8+4：0000 1100  最后一个 1 是 2^2 位上的 1，故 Lowbit(12) = 2^2 = 4；

8：0000 1000  最后一个 1 是 2^3 位上的 1，故 Lowbit(8) = 2^3 = 8；

代码实现：

int Lowbit(int x){
	return x&(-x);
}

 常用操作

• 更新元素

更新树状数组中元素的值

当我们读入A[1]，在更新C[1]的同时，还需要向上更新 C[2]，C[4]，C[8]，写为二进制 C[(001)]，C[(010)]，C[(100)]，C[(1000)]

lowbit = 1(001) C[1]+=A[1]

lowbit = 1+lowbit(1) = 2(010)  C[2]+=A[1]

lowbit = 2+lowbit(2) = 4(100)  C[4]+=A[1]

lowbit = 4+lowbit(4) = 8(1000) C[8]+=A[1]

当我们读入A[2]，在更新C[2]的同时，还需要向上更新 C[4]，C[8]，写为二进制 C[(010)]，C[(100)]，C[(1000)]

lowbit = 2(010)  C[2]+=A[2]

lowbit = 2+lowbit(2) = 4(100)  C[4]+=A[2]

lowbit = 4+lowbit(4) = 8(1000) C[8]+=A[2]

……

注意观察下标的变化，C[(001)]，C[(010)]，C[(100)]，C[(1000)]正是 Lowbit 从 1 一直累加之后的结果。 

代码实现：

void update(int x,int y){ //将y加到x位置上
    for(int i = x; i <= n; i+=lowbit(i))
        c[i] += y;//向上更新父结点
}

• 求前缀和

前缀和是一个数组的某项下标之前(包括此项元素)的所有数组元素的和。

举例：i = 7

sum[7] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;

前 i 项和 C[4]=A[1]+A[2]+A[3]+A[4];  C[6]=A[5]+A[6];  C[7]=A[7];

可以推出: sum[7] = C[4]+C[6]+C[7];

序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];

求区间 [a, b] 的区间和时，可以用 sum[b] - sum[a-1] 来计算

注意观察下标的变化，C[(111)]，C[(110)]，C[(100)] 正是 Lowbit 从 7 做减法到 6 到 4 最后到 0 之后的结果。

代码实现：

int sum(int x){
    int sum = 0;
    for(int i = x; i > 0; i-=lowbit(i))
        sum += c[i];
    return sum;
}

实战

 

1535	【例 1】数列操作
1536	【例 2】数星星 Stars
1537	【例 3】校门外的树
1538	清点人数
1539	简单题
1540	打鼹鼠_二维树状数组

参考博客：https://blog.csdn.net/weixin_44777363/article/details/107254870