一、算法概述
(1)优点:精度高、对异常值不敏感、无数据输入假定
(2)缺点:计算复杂度高、空间复杂度高
(3)使用数据范围:数值型和标称型
二、工作原理
存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似的数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数组多的分类,作为新数据的分类。
三、算法实例
(1)已有数据:
group=array([[1.0,0.9],[1.0,1.0],[0.1,0.2],[0.0,0.1],[1.0,1.1],[0.8,0.6],[1.2,1.0],[0.5,0.5]])
labels=['A','A','A','A','B','B','B','B']
两组待分类数据:
[1.2,1.1]
[0.1,0.1]
求两组待分类数据分别属于哪一类?
(2)算法伪代码:
对未知类别属性的数据集中的每个点依次执行以下操作:
1)计算已知类别数据集中的点与当前点之间的距离;
2)按照距离递增次序排序;
3)选取与当前点距离最小的k个点;
4)确定前k个点所在类别的出现频率;
5)返回前k个点出现频率最高的类别作为当前点的预测分类。
(3)代码详情
from numpy import *
import operator
import matplotlib.pyplot as plt
plt.figure(1)
plt.figure(2)
def createDataSet(): #创建一个数据集包含8个样本有2类
group = array( [ [1.0, 0.9], [1.0, 1.0], [0.1, 0.2], [0.0, 0.1], [1.0, 1.1], [0.8, 0.6], [1.2, 1.0], [0.5, 0.5]] ) #创建一个矩阵的每一行作为一个样本
labels = ['A', 'A', 'A', 'A', 'B', 'B', 'B', 'B'] #八个样本和两个类
return group, labels
def classify0(inX, dataSet, labels, k):
#inX:待分类数据集
#dataSet:已有数据集,通过createDataSet()函数获取
#labels:已有数据集对应的分类标签,通过createDataSet()函数获取
#k:设置最小距离数
dataSetSize = dataSet.shape[0] #获取数据集的行数
#计算距离
#tile(a,(b,c)):将a的内容在行上重复b次,列上重复c次
#下面这一行代码的结果是将待分类数据集扩展到已有数据集同样的规模,然后再与已有数据集作差
diffMat = tile(inX, (dataSetSize,1)) - dataSet
sqDiffMat = diffMat**2 #对上述差值求平方
sqDistances = sqDiffMat.sum(axis=1) #对于每一行的数据求和
distances = sqDistances**0.5 #对上述结果开方
sortedDistIndicies = distances.argsort() #对开方结果建立索引
#计算距离最小的k个点的Label
classCount={} #建立空字典,类别字典,保存各类别的数目
for i in range(k): #通过循环寻找k个近邻
voteIlabel = labels[sortedDistIndicies[i]] #先找出开方结果索引表中第i个值对应的Label值
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 #存入当前label以及对应的类别值
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) #对类别字典进行逆排序,级别数目多的往前放
return sortedClassCount[0][0] #返回级别字典中的第一个值,也就是最有可能的Label值
a=input('待分类数据的x坐标:')
b=input('待分类数据的y坐标:')
p=[1.0, 1.0, 0.1, 0.0]
q=[0.9, 1.0, 0.2, 0.1]
r=[1.0, 0.8, 1.2, 0.5]
s=[1.1, 0.6, 1.0, 0.5]
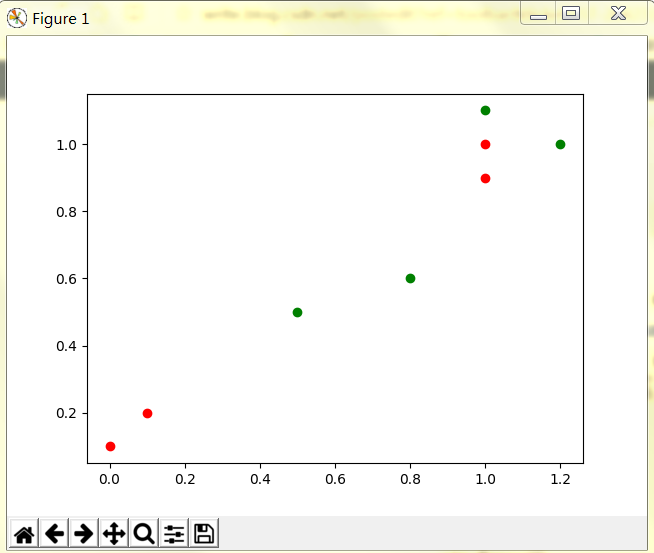
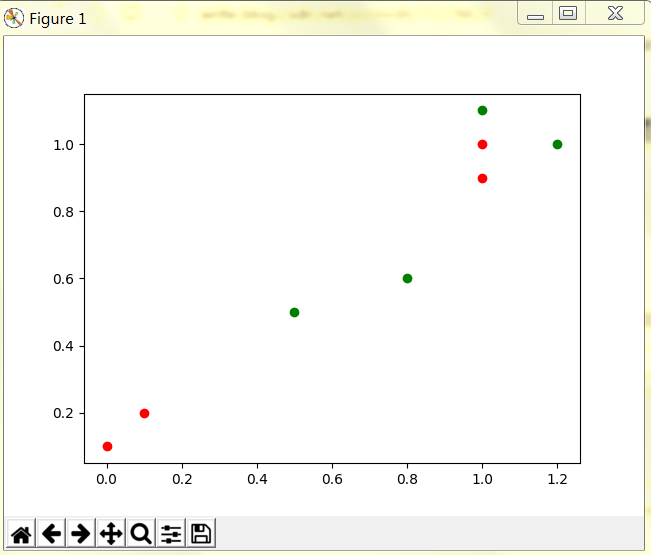
plt.figure(1) #生成散点图
plt.plot(p,q,'or')
plt.plot(r,s,'og')
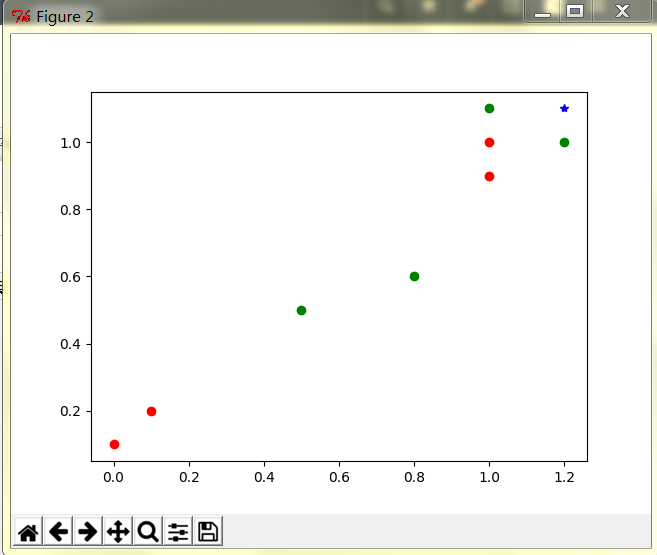
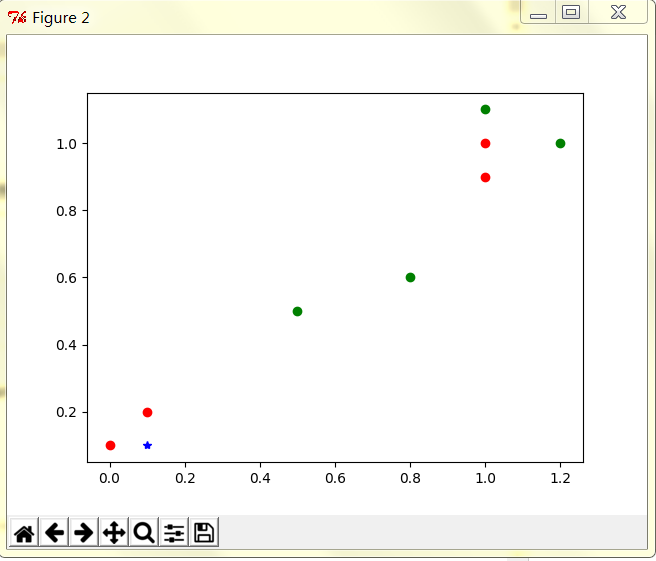
plt.figure(2)
plt.plot(p,q,'or')
plt.plot(r,s,'og')
plt.plot(a,b,'b*')
plt.show()
待分类数据的x坐标:1.2
待分类数据的y坐标:1.1
输入
待分类数据的x坐标:0.1
待分类数据的y坐标:0.1
输出
四、算法小结
k-近邻算法时分类数据最简单最有效的算法。k-近邻算法是基于实例的学习,使用算法我们必须有接近实际数据的训练样本数据。k-近邻算法必须保存全部数据集,如果训练数据集很大,必须使用大量的储存空间。此外,由于必须对数据集中的每一个数据计算距离值,实际使用时可能非常耗时。
k-近邻算法的另一个缺陷是它无法给出任何数据的基础结构信息,因此我们也无法知晓平均实例样本和典型实例样本局有什么特征。






















 1450
1450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








