softmax回归

1.Softmax回归

Softmax回归是一种常用的分类模型，常用于多分类问题。它可以将一个实例映射为各个类别的概率分布，从而使得每个类别的概率之和为1。

Softmax回归的基本思想是首先对每个类别计算一个分数（score），然后将分数转化为概率。具体地，给定一个输入样本 $\mathbf{x}$，Softmax回归首先对每个类别 $j$ 计算一个分数 $z_j={\mathbf{w}}_j^T\mathbf{x}+b_j$，其中 ${\mathbf{w}}_j$ 和 $b_j$ 分别是第 $j$ 个类别的权重和偏差，${\mathbf{w}}_j$ 和 $\mathbf{x}$ 都是向量。然后，将每个类别的分数通过 softmax 函数转化为概率：

$$\hat{y}j=\frac{e^{z_j}}{\sum {k=1}^K{e}^{z_k}}$$

其中 ${\hat{y}}_j$ 是样本属于第 $j$ 个类别的概率估计值，$K$ 是总共的类别数。Softmax 函数可以将分数转化为概率，使得所有类别的概率之和为1。

在训练Softmax回归模型时，通常采用最大似然估计法来估计模型参数。给定一个训练集 $\mathcal{D}=(\mathbf{x}i,y_i){i=1}^n$，其中 ${\mathbf{x}}_i$ 是样本的特征向量，$y_i$ 是样本的类别标签。假设每个样本属于某个类别的概率是 ${\hat{y}}_i$，则对于样本 $({\mathbf{x}}_i,y_i)$，其似然函数可以定义为：

$$L(\mathbf{w},\mathbf{b})=\prod _{i=1}^K\prod _{j=1}^n({\hat{y}}_i^{(j)}{)}^{[y_i=j]}$$

其中 ${\hat{y}}_i^{(j)}$ 是样本 ${\mathbf{x}}_j$ 属于类别 $i$ 的预测概率，$[y_i=j]$ 是一个指示函数，当 $y_i=j$ 时其值为1，否则为0。将上式取负对数，则可得到 Softmax 回归的损失函数：

$$J(\mathbf{w},\mathbf{b})=-\sum _{i=1}^n\sum _{j=1}^K[y_i=j]\log {\hat{y}}_i^{(j)}$$

该损失函数可以通过梯度下降等优化算法来最小化。

2.Softmax函数

Softmax函数是一种常用的激活函数，主要用于将多个输入转换成一个归一化的概率分布输出。Softmax函数通常被用于多分类任务，例如图像分类、自然语言处理等领域。

假设我们有一个长度为 $n$ 的向量 $\mathbf{z}=(z_1,z_2,\dots ,z_n)$，其中 $z_i$ 表示第 $i$ 个类别的得分或概率，那么Softmax函数将每个得分转换成对应类别的概率，具体地，Softmax函数的计算公式为：

$$\text{Softmax}(z_i)=\frac{\exp (z_i)}{{\sum }_{j=1}^n\exp (z_j)}$$

其中 $i=1,2,\dots ,n$，$\exp (z_i)$ 表示 $z_i$ 的指数形式。Softmax函数的输出值是一个 $n$ 维向量 $\mathbf{p}=(p_1,p_2,\dots ,p_n)$，其中 $p_i$ 表示第 $i$ 个类别的概率。注意到，Softmax函数的输出值是一个概率分布，即 ${\sum }_{i=1}^n{p}_i=1$。

直观地说，Softmax函数的作用是将输入的得分或概率进行归一化，使得它们之间的大小关系得到保留，并且可以直接用来表示不同类别的概率。具体来说，Softmax函数对每个输入值进行指数运算，然后将指数值相加并进行归一化处理，得到每个类别的概率。

需要注意的是，Softmax函数对于输入的值域较大或较小的情况可能会存在数值上的不稳定性，容易出现数值溢出或数值下溢的问题。为了解决这个问题，通常需要对输入值进行适当的调整，例如减去输入向量中的最大值。此外，由于Softmax函数的输出值是一个概率分布，因此它可以与交叉熵损失函数结合使用，用于训练神经网络进行多分类任务。

3.最大似然估计法

最大似然估计法是一种用来估计参数的方法，它的基本思想是利用观测数据来确定未知参数的值，使得这些参数能够最好地解释观测到的数据。在实际应用中，我们通常假设观测数据来自于一个已知的概率分布，而这个概率分布的参数则是我们需要估计的未知参数。

假设我们有一组观测数据 $x_1,x_2,\dots ,x_n$，并且我们已经确定了这些数据来自于一个概率分布 $f(x;\theta )$，其中 $\theta$ 是需要估计的未知参数。那么，最大似然估计法的目标就是找到一个参数值 $\theta$，使得给定这个参数值时，这组观测数据出现的概率 $L(\theta ;x_1,x_2,\dots ,x_n)$ 最大。

具体地，我们可以将 $L(\theta ;x_1,x_2,\dots ,x_n)$ 定义为给定参数 $\theta$ 时，观测数据 $x_1,x_2,\dots ,x_n$ 出现的联合概率密度函数，即

$$L(\theta ;x_1,x_2,\dots ,x_n)=\prod _{i=1}^{n}f(x_i;\theta )$$

然后，我们的任务就是求解参数 $\theta$，使得 $L(\theta ;x_1,x_2,\dots ,x_n)$ 最大。这个过程可以使用一些数值优化方法来完成，例如梯度下降、牛顿法等。

需要注意的是，最大似然估计法的结果通常是一个点估计，即一个具体的参数值，而不是一个参数分布。因此，我们得到的估计结果可能存在偏差，并且可能不包含任何不确定性信息。为了更好地描述参数的不确定性，我们通常会使用贝叶斯统计方法，得到参数的后验分布，从而获得更全面的估计结果。

通俗一点：
从箱子里面有黄球和白球一共10个。每次从箱子里面拿出一个，记录10次，结果为8白2黄。

很明显，第二种假设的概率更高，所以8白2黄的可能性最大。
进一步分析

对$$\underset{0<p<1}{\mathrm{argmax}}(p^8(1-p{)}^2)$$求导得p=0.8。

4.指示函数

指示函数（Indicator Function）是一种数学函数，通常用于表示一个特定条件是否满足。指示函数的输出为0或1，其中当特定条件成立时输出1，否则输出0。

形式上，如果$A$是一个集合，$1_A$表示指示函数，定义如下：

$$1_A(x)=\{\begin{array}{llc}1& x\in A，0& x\notin A\end{array}$$

指示函数也可以表示为符号函数的特例，其中符号函数的输出为-1、0或1，取决于参数的正负号。指示函数的输出只有0或1，通常用于简化数学公式或证明中的推理过程。

在概率论和统计学中，指示函数经常用于表示事件是否发生，例如，在一个离散随机变量$X$的分布中，可以用指示函数表示$X$取某个特定的值$k$的概率：

$$P(X=k)=\mathbb{E}[1_{X=k}]$$

指示函数还可以用于计算集合的大小，例如，一个集合$A$中元素的个数可以表示为：

$$|A|=\sum _{x\in A}1$$

指示函数的应用非常广泛，不仅在概率论、统计学和数学分析中有重要作用，而且在计算机科学、物理学、经济学、社会学等领域也有广泛应用。

5.信息熵

信息的作用是消除不确定性。information

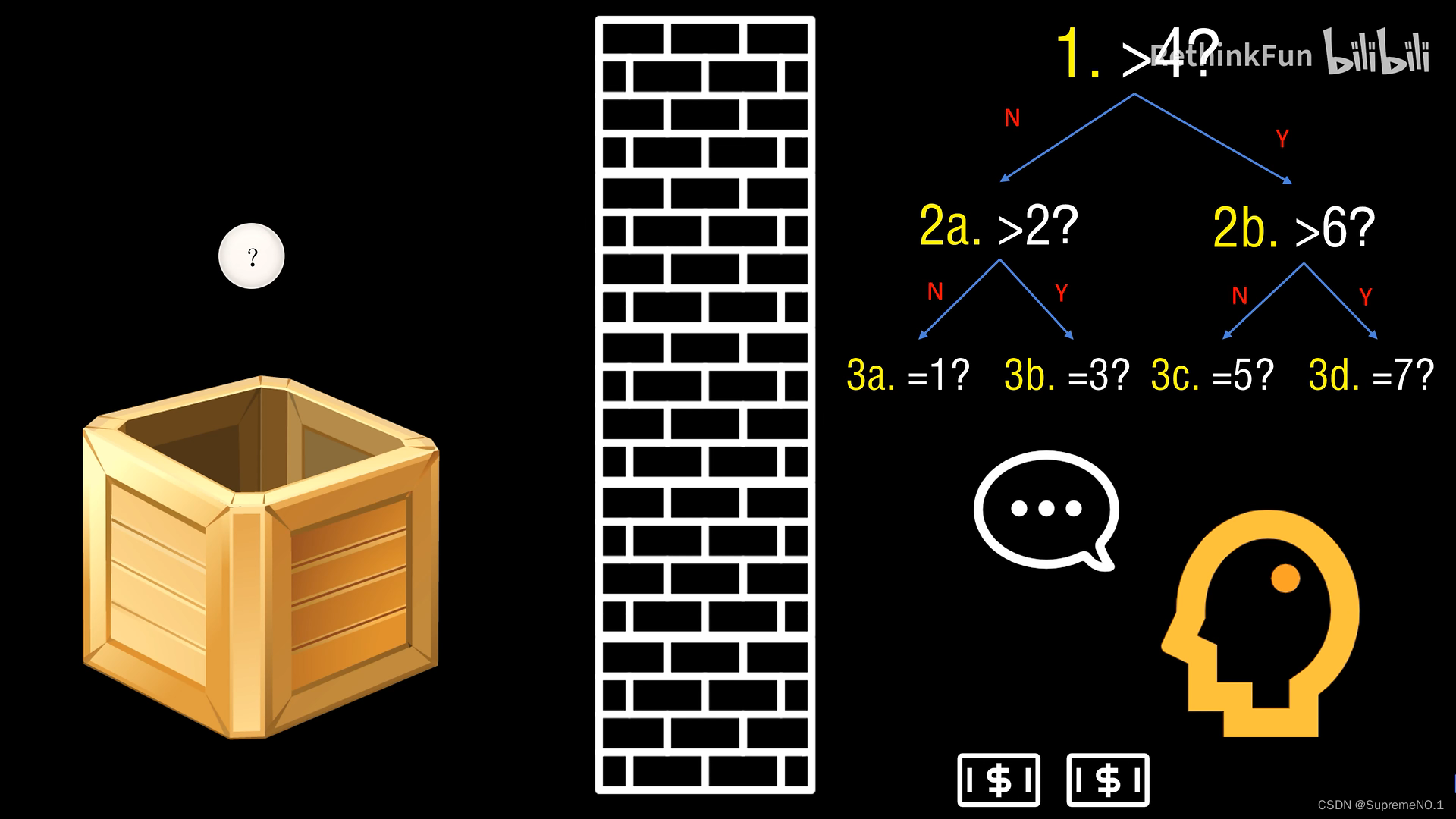
假如有个朋友给你扔骰子，并且给你说了三句话。
第一句话：“骰子的点数大于0”（废话）
第二句话：“骰子的点数大于3”（一半废话）
第三句话：“骰子的点数是5”（非常有用）

第一句话没有消除任何你对骰子点数的不确定性
第二句话消除了你对骰子一半的不确定性
第三句话完全能消除了你对骰子的不确定性

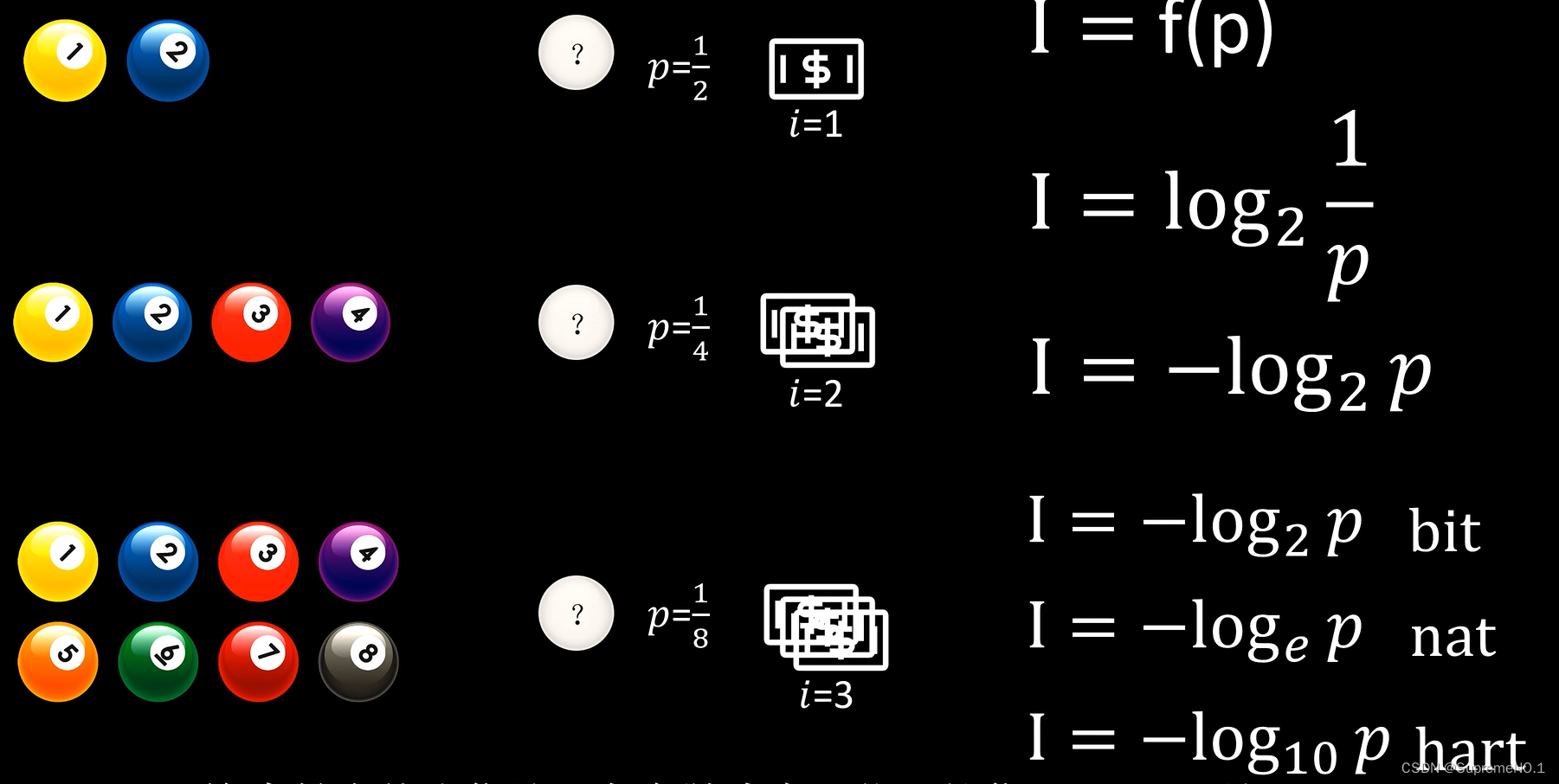
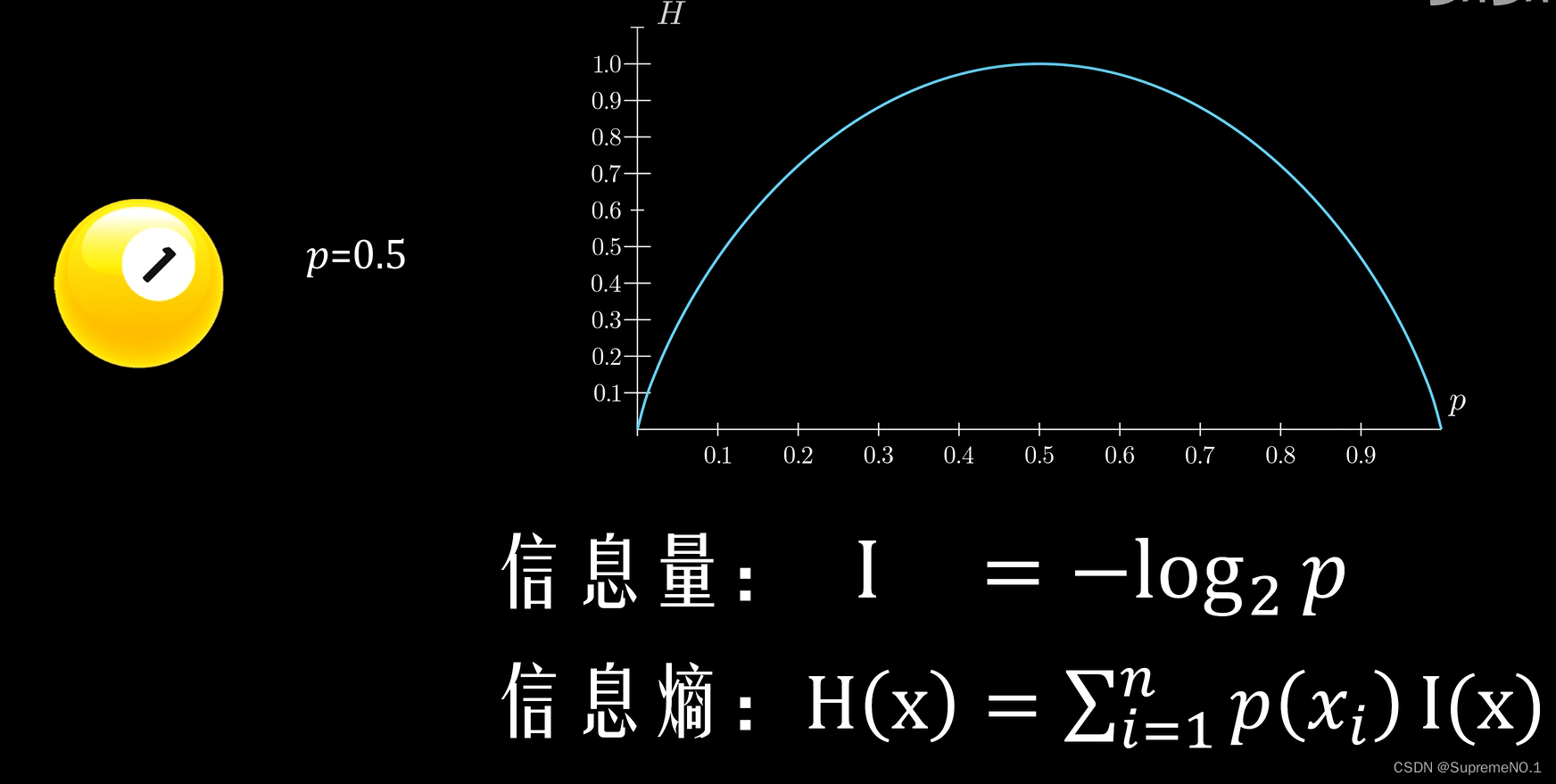
怎么度量信息量？