最大公共子序列LCS

概述

什么是子序列？

对于一个序列，去掉其中n个序列项(n>=0)，剩下的就是子序列。注意和子串区别，子串是要求要连续的。

利用DP解决LCS问题：

• 状态描述：lcs[i][j] 表示对于输入的两个字符串s1,s2，s1的前i个子串和s2的前j个子串的最大公共子序列长度。
• 最优子结构：当s[i]=s[j]，lcs[i][j]=l[i-1][j-1]+1;否则：lcs[i][j]=max(lcs[i-1][j],lcs[i][j-1]);
• 边界：i=0或者j=0，lcs[i][j]=0;

关键代码

#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
using namespace std;
int lcs[1001][1001];

void maxLcs(string& s1,string& s2)  // 最大公共子序列dp
{
    int n=s1.length();
    int m=s2.length();
    memset(lcs,0,sizeof(lcs));

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(s1[i-1]==s2[j-1])
                lcs[i][j]=lcs[i-1][j-1]+1;
            else{
                lcs[i][j]=max(lcs[i-1][j],lcs[i][j-1]);
            }
        }
    }
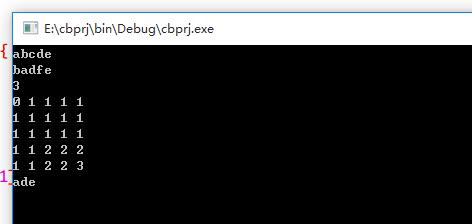
    cout<<lcs[n][m]<<endl;
    // 打印状态矩阵
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cout<<lcs[i][j]<<" ";
        }
        cout<<endl;
    }

    // 输出最长子序列
    string s3;
    for(int i=n,j=m;i>=1 && j>=1;){
        if(s1[i-1]==s2[j-1]){
            s3+=s1[i-1];
            i--;
            j--;
        }
        else if(lcs[i][j-1]>lcs[i-1][j]){
            j--;
        }
        else
            i--;
    }
    reverse(s3.begin(),s3.end());

    cout<<s3<<endl;

}

int main() {
    string s1;
    string s2;
    while(cin>>s1>>s2){
        maxLcs(s1,s2);
    }

    return 0;
}

//abcda

运行截图