RMQ | ST 表 | 树状数组 学习笔记

前言

前段时间没啥空写博客，今天汇总一下这几天学的几种数据结构。

Part1. ST 表

ST 表是用于求解 RMQ（区间最值） 问题的一种数据结构，使用了倍增的思想，时间复杂度 $\mathcal{O}(n\log n)$。

本人认为 ST 表很类似区间 dp。

有一个数组 $a$，假设现在要求静态区间最大值。

I. 创建 ST 表

首先定义 ST 表 $s{t}_{i,j}$ 表示 $[i,i+2^j-1]$ 这段区间的最大值。数学公式有点别扭，说白了就是以 $i$ 开始的 $2^j$ 个数中的最大值。

由于 $2^0=1$，所以 $s{t}_{i,0}$ 就是 $a_i$（差不多是 dp 的边界条件吧）。

然后，我们要由小区间推出大区间，看图：

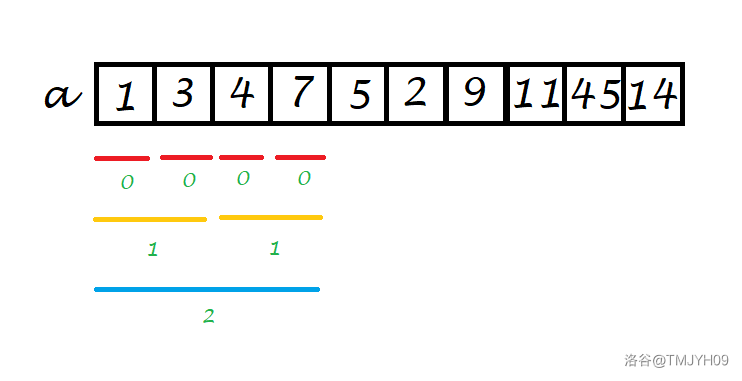
绿色数字代表 $j$ 值。可见，$s{t}_{i,j}$ 是由两个小区间推出来的，很容易得到状态转移方程：

$$s{t}_{i,j}=\max (s{t}_{i,j-1},s{t}_{i+2^{j-1},j-1})$$

现在就类似区间 dp 那样，先枚举区间长度 $j$，再枚举左端点 $i$。

ST 表的创建代码如下：

for(int j=1;(1<<j)<=n;j++){
    for(int i=1;i+(1<<j)-1<=n;i++){
        st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]);
    }
}

对 $i$ 和 $j$ 枚举范围的解释：

• $j$ 作为区间长度，自然不能超过 $n$。

• $i$ 作为左端点，我们知道 $s{t}_{i,j}$ 表示的区间是 $[i,i+2^j-1]$，不能超过 $n$。

II. 求解 RMQ

创建好 ST 表，就要充分地利用它。

对于查询的区间 $[l,r]$，组成它的两段子区间长度的指数 $k={\log }_2(r-l+1)$。

故答案为两段的最大值。

第一段就是 $[l,k]$，但是第二段有点麻烦了。

由于 $r-l+1$ 不一定满足 ${\log }_2(r-l+1)\in \mathbb{N}$，所以两段区间会有重合的部分，这不影响最终的结果，但是左端点就要由 $r$ 推出来，即 $r-2^k+1$。

第二段区间就是 $[r-2^k+1,k]$。

求解 RMQ 代码如下：

int k=log2(r-l+1);
writeln(max(st[l][k],st[r-(1<<k)+1][k]));

总结

ST 表运用的倍增思想，可以说跟分治有异曲同工之妙（虽然完全就不同）。

前者不断地将指数增加，求解 $2^0$，$2^1$，$2^2$ 等子问题，再推出大问题。

后者呢是一个大问题，不断地二分下去（或者划成更多子问题）。

ST 表在 LCA 问题中也有广泛的运用。

Part2. 树状数组

最基本的树状数组可以维护单点修改、区间查询的问题，时间复杂度在 $\mathcal{O}(\log n)$，且常数较小。

树状数组运用了差分思想。

树状数组非常的优美，不像隔壁线段树，我 *@%^~?*#…，码量和常数都很大（相对树状数组）。

树状数组核心就 3 个函数，不过呢需要理解一个非常重要的点：lowbit。

简单来说，一个数的 lowbit 就是这个数在二进制下最低位的 $1$ 所对于的值，例如 $(6{)}_{10}=(110{)}_2$，那么它的 lowbit 就是 $2$。

lowbit 函数可以用如下代码实现：

inline int lowbit(int i){return i&-i;}

非常简洁。

树状数组直接用一个 $c$ 表示即可，简单到我都不用专门建一个小节出来。

I. 单点修改

代码如下：

void add(int i,int k){for(;i<=n;i+=lowbit(i))c[i]+=k;}

II. 区间查询

树状数组可以简单维护前缀和。

代码如下：

int sum(int i){
    int s=0;
    for(;i;i-=lowbit(i))s+=c[i];
    return s;
}

至于区间查询，结合前缀和的思想即可写出来了。

拓展

树状数组有个很奇妙的用途就是求逆序对。

将树状数组当成一个加强的桶，每插入一个数 $a_i$，先给 $c_{a_i}\leftarrow c_{a_i}+1$，答案就加上 $i-\sum _{j=1}^{a_i}{a}_j$ 即可。

那么，为什么？

$c_{a_i}\leftarrow c_{a_i}+1$：就是 $a_i$ 的出现次数增加了 $1$，不要把这里的 $c$ 当树状数组，当成一个普通的桶即可。

$i-\sum _{j=1}^{a_i}{a}_j$：到目前出现了 $i$ 个数，减去小于它的数的出现次数。

如果是 P1908 的话还需要离散化处理，这里不细说了。

代码实现：

int ans=0;
for(int i=1;i<=n;i++){
    a[i]=read();
    add(a[i],1);
    ans+=i-sum(a[i]);
}

总结

之后的树套树，若是树状数组的话，处理起来会比线段树、平衡树简单很多。

但是呢它简便，维护的东西自然少，树状数组能维护的东西，线段树都能维护。

至于求逆序对，理解还是有点困难的（至少对于我），理解之后会发现非常的巧妙。