第6.1节
最少2^h,最多2^(h+1)−1。可以看出,因为深度为h−1的完全二叉树有
个元素,深度为h的堆中元素个数介于深度为h−1不包含的完全二叉树的个数和深度为h包含的完全二叉树的个数之间。
Exercise 6.1-2
![]()
设n = 2^m − 1+k,其中m尽量大。然后堆由高度为m−1的完整二叉树组成,以及底部的k个附加叶子。根的高度就是到这k个叶节点的最长简单路径的长度,它的长度一定是m,从我们定义m的方式可以清楚地看出
。
Exercise 6.1-3
![]()
如果子树中最大的元素不在根树中,那么它在子树中有一个父元素。所以,它比它的父结点大,所以,在子树中最大元素的父结点处违反了堆属性。
Exercise 6.1-4
![]()
最小的元素必须是一个叶子节点。假设节点x包含最小的元素并且x不是叶节点。设y为x的一个子节点。根据max-heap的性质,x的值大于等于y的值。由于堆的元素是不同的,所以不等式是严格的。这与x包含堆中最小元素的假设相矛盾。
Exercise 6.1-5
![]()
是的。子节点的索引总是大于父节点的索引,因此每个顶点都满足堆属性。
Exercise 6.1-6
![]()
不,这个数组不是最大堆。7包含在数组的第9个位置,因此它的父元素必须在包含6的第4个位置。这违反了max-heap属性。
Exercise 6.1-7
![]()
这足以说明没有子元素的元素精确地以
为索引。假设在这个范围内有一个i。它的子节点将位于2i和2i+ 1,但它们都
,因此不在数组中。现在,假设我们有一个没有子元素的元素,这意味着2i和2i + 1都> n,然而,这意味着i > n/2。这意味着
第6.2节
Exercise 6.2-1

Exercise 6.2-2

MIN-HEAPIFY的运行时间与MAX-HEAPIFY相同。
Exercise 6.2-3
![]()
数组保持不变,因为第8行的if语句将为假。
Exercise 6.2-4![]()
如果i > A.heap - size/2,那么l和r都将超过A.heap - size,因此算法第3行和第6行的if语句条件将永远不会满足。因此,largest= i,因此永远不会进行递归调用,也不会发生任何事情。这是有意义的,因为i必须对应于一个叶节点,所以MAX-HEAPIFY不应该改变堆。
Exercise 6.2-5

Exercise 6.2-6

考虑由A生成的堆,其中A[1] = 1, A[i] = 2,当2≤i≤n时。由于1是堆中最小的元素,因此必须通过堆的每一级交换它,直到它成为叶节点。由于堆的高度为
, MAX-HEAPIFY的最坏情况时间为Ω(lg n)。
第6.3节
Exercise 6.3-1

Exercise 6.3-2

如果我们从1开始,我们将无法保证max-heap属性得到维护。例如,如果数组A是由[2,1,1,3]给出的,那么MAX-HEAPIFY不会与它的任何一个子元素交换2,两个都是1。然而,当在左子元素1上调用MAX-HEAPIFY时,它将用3交换1。这违反了最大堆属性,因为现在2是3的父结点。
Exercise 6.3-3
![]()
高度为h的所有节点将叶节点集划分为大小介于2^(h−1) + 1和2^h之间的集合,其中除一个节点外,其他节点的大小均为2^h。只需将每个分区的所有子分区放在它们各自的分区中。回想一下6.1-2,堆的高度是
,所以,通过观察这个高度的一个元素(根),我们得到最多有
个叶节点。由于每一个高度为h的顶点都将其划分为至少2^(h - 1) + 1的部分,并且除了一个点以外,其余部分都对应2^h的部分,我们可以让k表示我们想要绑定的量, 因此
因此,

第6.4节
Exercise 6.4-1

Exercise 6.4-2
我们将用归纳法证明HEAPSORT的循环不变量:
基本情况:在第2-5行for循环的第一次迭代开始时,我们有i = A.length。子数组A[1...n]是一个最大堆,因为BUILD-MAX-HEAP(A)刚刚被调用。它包含n个最小的元素,以及空子数组A[n+1...n]平凡地包含A中排序后最大的0个元素。
假设在第2-5行for循环的第i次迭代开始时,子数组A[1...i]是包含A[1...n]中第i个最小元素的最大堆,和子数组A[i + 1...n]包含A的n−i个最大的元素A[1...n]。自从A[1...i]是一个最大堆,A[1]是A[1…i]中最大的元素。因此,它是原始数组中第(n−(i−1))个最大的元素,因为已经假定第n−i个最大的元素位于数组的末尾。第3行将A[1]与A[i]交换,因此A[i...n]包含数组中最大的n−i + 1个元素,和A[1..i−1]包含i−1个最小的元素。最后,用A, 1上调用MAX-HEAPIFY。因为A[1...i]在迭代之前是一个最大堆,并且只有位置1和i的元素被交换,节点为1的左右子树,直到节点为i - 1,将是最大堆。对MAX-HEAPIFY的调用将把现在位于节点1的元素放置到正确的位置并恢复max-heap属性,以便A[1..i−1]为最大堆。这样就结束了下一次迭代,并且我们已经验证了循环不变式的每个部分。通过归纳,循环不变式适用于所有迭代。
在最后一次迭代之后,循环不变量表示子数组A[2...n]包含A的n−1个最大元素A[1...n],已排序。因为A[1]一定是第n大的元素,所以整个数组必须按照期望排序。
Exercise 6.4-3

如果它已经按递增顺序排序,那么在第1行执行BUILD-MAX-HEAP调用将花费Θ(n lg(n))时间。当我们在BUILD-HEAP中调用MAX-HEAPIFY(A,i)时,我们知道A[i]比它右边的所有元素都大。这意味着它花费的时间是
。所以构建堆的总时间是
在HEAPSORT中将有n次for循环迭代,每次迭代花费Θ(lg(n))时间,因为位于位置i的元素是最小的,因此在第5行执行MAX-HEAPIFY时将有
步。也就是Θ(nlg (n))时间。
如果它已经按降序排序,那么对第一行的调用只需要Θ(n)时间,因为它一开始就已经是一个最大堆了。这是因为位于较早位置的元素对应于在堆中更靠前的位置,并且由于数组是降序的,因此这些元素具有更大的值。因此,BUILD-MAX-HEAP过程中的每个MAX-HEAPIFY调用将只花费常数时间,因为MAX-HEAPIFY的第8行检查总是为假。它仍然需要nlg (n)从堆中剥离元素并重新堆化。这是因为每次我们交换堆头和最后一个元素时,我们现在有最小的元素在头部,所以它必须有与堆深度一样多的MAX-HEAPIFY递归调用,这大约是lg(n)。
Exercise 6.4-4
![]()
考虑对按降序排序的数组调用HEAPSORT。每次A[1]与A[i]交换时,MAX-HEAPIFY将被递归调用的次数等于包含位置1到i - 1的元素的最大堆的高度h,并且运行时间为O(h)。由于高度k处有2^k个节点,运行时的边界如下
Exercise 6.4-5
![]()
由于第一行的调用可能只需要线性时间(例如,如果输入已经是一个max-heap),我们将重点展示for循环需要n*logn时间。之所以会出现这种情况,是因为每次最后一个元素被放置在开始位置以取代被移除的最大元素时,它必须遍历每一层,因为它已经很小了,因为它之前在堆的最底层。
第6.5节
Exercise 6.5-1

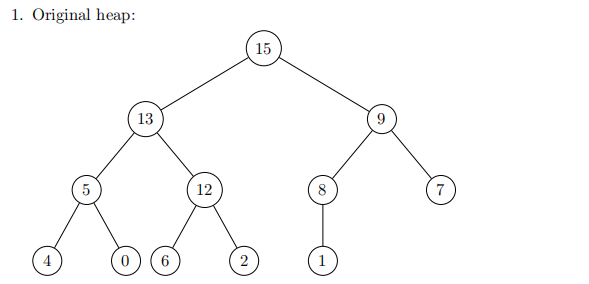
下面的图片序列显示了如何从堆中提取最大值。
1. 原始堆:
2. 我们把最后一个元素移到堆的顶端
3.13 > 9 > 1,我们交换1和13。
4. 因为12 > 5 > 1,我们交换1和12。
5. 因为6 > 2 > 1,我们交换1和6。
Exercise 6.5-2

下面的图片序列显示了如何将10插入到堆中,然后与父节点交换,直到恢复max-heap属性。包含新键的节点被重着色。
1. 原始堆:
2. 调用MAX-HEAP-INSERT(A,10),因此我们首先追加分配的节点价值−∞:
3.更新新节点的key值:
4. 由于父键小于10,节点被交换:
5. 由于父节点小于10,节点被交换:
Exercise 6.5-3

Exercise 6.5-4

如果我们不分配给A[A.heap - size]则它可以包含任何值。特别是,当我们调用HEAP-INCREASE-KEY时,可能会出现A[A.heap−size]初始值大于key,导致错误。通过将−∞赋值给A[A.heap−size]。我们保证不会发生错误。然而,我们可以将任何小于或等于key的值赋给A[A.heap−size],算法仍然可以工作。
Exercise 6.5-5

最初,我们有一个堆,然后只改变第i处的值,使它变大。这不能使i和它的子元素之间的顺序无效,唯一需要与i相关的是i小于它的父元素,这可能是假的。因此初始化时不变式为真。然后,当我们把i和它的父结点交换时如果它更大,因为它比它的父结点大,它也一定比它的兄弟结点大,同样,因为它的父结点在堆中最初比它的子结点高,我们知道它的父结点比它的子结点大。唯一有问题的关系是新的i和它的父结点。在终止时,i是根,所以它没有父节点,所以堆属性必须处处满足。
Exercise 6.5-6

在while条件中将A[i]替换为key,并将第5行替换为“A[i] =A[PARENT(i)]”。在while循环结束后,添加一行A[i] = key。因为键值不会改变,所以在我们知道它在堆中的位置之前,给它赋值是没有意义的。相反,我们只将父节点分配给子节点。在while循环结束时,i等于key所在的位置,因为它要么是根节点,要么父节点至少是key,所以我们进行赋值。
Exercise 6.5-7

在结构中添加一个字段,该字段只是对添加的元素总数进行计数。添加元素时,使用该计数器的当前值作为键。
Exercise 6.5-8

该算法的工作原理如下:将要删除的节点的键替换为∞,即一个将被解释为大于存储在max-heap中的所有其他键的值。调用HEAP-INCREASE-KEY将使该节点浮动到max-heap的顶部。然后,我们用堆中最后一个元素的值替换根节点的值,根据max-heap属性,已知根节点的值小于A[1]。我们更新堆的大小,然后调用MAX-HEAPIFY来恢复max-heap属性。它的运行时间为O(lgn),因为INCREASE-KEY的运行时间为O(lgn),并且递归调用MAX-HEAPIFY的次数与堆的高度相同,即
。
Exercise 6.5-9

从k个表的每一个表的头构造一个最小堆。然后,为了在排序数组中找到下一个元素,提取最小元素(在O(lg(k))时间内)。然后,从较短的列表中添加下一个元素到堆中(也是O(lg(k))时间)。由于查找排序列表中的下一个元素最多只需要O(lg(k))时间,因此查找整个列表需要O(n lg(k))个总步骤。














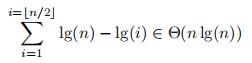






























 1126
1126

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








