PARTITION代码

第7.1节
Exercise 7.1-1

Exercise 7.1-2
如果数组中所有元素的值相同,则PARTITION返回r。为了使PARTITION在所有元素的值相同时返回
,修改算法第4行如下:如果A[j]≤x且j(mod2) = (p + 1)(mod2)。这导致算法将相同值的一半实例算作小于,另一半算作大于。
Exercise 7.1-3
![]()
for循环精确地进行r - p次迭代,每次迭代最多占用常数时间。for循环之外的部分最多占用常数时间。由于r−p是子数组的大小,因此PARTITION所花费的时间最多与调用它的子数组的大小成正比。
Exercise 7.1-4
![]()
要修改QUICKSORT以非递增顺序运行,我们只需要修改PARTITION的第4行,将≤改为≥。
第7.2节
Exercise 7.2-1

通过Θ的定义,我们知道存在c1,c2,使得Θ(n)项在c1*n和c2*n之间。我们让归纳假设是c1* m^2 ≤ T(m) ≤ c2* m^2对于所有m < n,那么,对于足够大的n,
Exercise 7.2-2![]()
对于每个元素都具有相同值的数组,快速排序的运行时间为n^2。这是因为分区总是发生在数组的最后一个位置(练习7.1-2),所以算法表现出最坏情况的行为。
Exercise 7.2-3

如果数组已经按降序排序,则枢轴元素小于所有其他元素。划分步骤花费Θ(n)时间,然后留给您一个大小为n - 1和大小为0的子问题。这就得到了7.2-1中考虑的递归式。它的解是Θ(n^2)。
Exercise 7.2-4
我们说,“几乎已排好序”的意思是,对于某个常数c, A[i]离它在排序数组中的正确位置最多c个位置。对于INSERTION-SORT,在找到外部for循环的任何特定迭代插入A[j]的位置之前,我们最多运行c次内部while循环。因此,运行时间为O(cn) = O(n),因为c是预先固定的。现在假设我们运行快速排序。PARTITION的分割最多从n−c到c,这将导致O(n^2)的运行时间。
Exercise 7.2-5

最小深度对应于重复取较小的子问题,即大小与α成正比的分支。然后,这将在k步中下降到1,其中
。
。最长深度对应于总是取较大的子问题。然后我们得到一个相同的表达式,用1−α代替α。
Exercise 7.2-6

在不丧失一般性的前提下,假设输入数组的条目是不同的。由于只有条目的相对大小有关系,我们可以假设A包含数字1到n的随机排列。现在固定0 < α ≤1/2。设k表示A中小于A[n]的元素个数。当且仅当αn≤k≤(1−α)n时,分割产生比1−α到α更平衡的分裂。这种情况发生的概率是
。
第7.3节
Exercise 7.3-1

我们分析预期运行时间,因为它代表了更典型的时间成本。此外,我们对计算过程中可能使用的随机性进行预期运行时间计算,因为它不能以对抗性的方式产生,这与对算法的所有可能输入进行预期运行时间计算不同。
Exercise 7.3-2

在这两种情况下,Θ(n)调用RANDOM。在最好的情况下,PARTITION会运行得更快,因为输入通常会更小,但是每次调用RANDOMIZED-PARTITION都会调用RANDOM,这发生Θ(n)次。
第7.4节
Exercise 7.4-1

通过Θ的定义,我们知道存在c1,c2,使得Θ(n)项在c1n和c2n之间。我们让归纳假设是c1* m^2 ≤ T(m) ≤ c2* m^2,对于所有m < n,那么,对于足够大的n,
另一个方向也是一样。
Exercise 7.4-2
![]()
我们将使用代换法来证明最佳情况下的运行时间是Ω(nlgn)。设T(n)是对大小为n的输入进行快速排序的最佳情况时间。我们有了递归式
假设T(n)≥c(nlgn + 2n)对于某个常数c,把这个猜想代入递归式得到
对q求导表明,当q = n/2时得到最小值。取c大到足以支配- lgn + 2 - 2c + Θ(n)项使得它大于cn lgn,证明了边界。
Exercise 7.4-3

我们把给定的表达式看作是连续的q,然后,任何极值必须相邻于一个临界点,或者是其中一个端点。关于q的二阶导数是4,所以我们找到的任何临界点都是最小值。这个表达式对q的导数是2q - 2(n - q - 2) = - 2n + 4q + 4当2q + 2 =n时它等于零,所以在q =(n - 2)/2处有一个极小值。所以最大值只能是端点。我们可以看到端点是相等的,因为在q = 0时,它是(n−1)^2,而在q = n−1时,它是(n−1)^2 + (n−n + 1−1)^2 = (n−1)^2。
Exercise 7.4-4
![]()
对于本节给出的预期运行时间,我们将使用下界(A.13):
因为lg(n!) = Θ(nlgn)通过练习3.2-3。因此RANDOMIZED-QUICKSORT的预期运行时间为Ω(nlgn)。
Exercise 7.4-5

如果我们只在问题大小≤k之前进行快速排序,那么,我们将不得不采取lg(n/k)步,因为在随机化快速排序的原始分析中,我们期望递归树有lg(n)个层次。因为我们只是对整个数组调用快速排序,我们知道每个元素都在其最终位置的k以内。这意味着对于每个需要改变位置的元素,插入排序最多需要移动k个元素。这就得到了所描述的运行时间。
理论上,我们应该选择k来最小化这个表达式,也就是说,对k求导,我们希望它的值为0。所以n− n/k = 0,所以
。比例常数取决于n*k项和nlg (n/k)项中常数的相对大小。在实践中,我们会尝试使用大量的输入大小来获取不同的k值,因为这里没有考虑到机器的一些粗糙属性,比如缓存行大小。
Exercise 7.4-6

为了分析的简单性,我们将假设数组A中的元素是数字1到n。如果我们让k表示中位数,则α到1−α分裂的最坏情况的概率是αn≤k≤(1−α)n的概率。“坏”三元组的数量等于至少两个数字来自[1,αn]或至少两个数字来自[(1−α)n, n]的三元组的数量。由于两个区间具有相同的大小,因此坏三元组的概率为
。因此,选择一个“好的”三组,从而在最坏的情况下得到α到1−α分裂的概率为












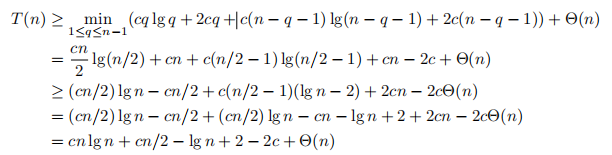
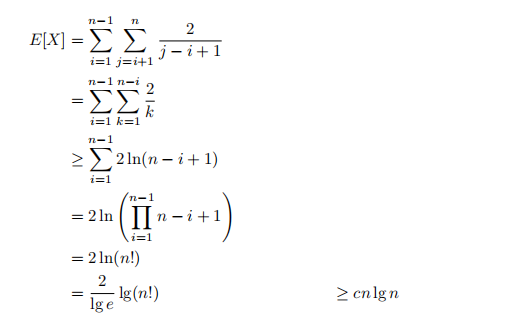













 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








