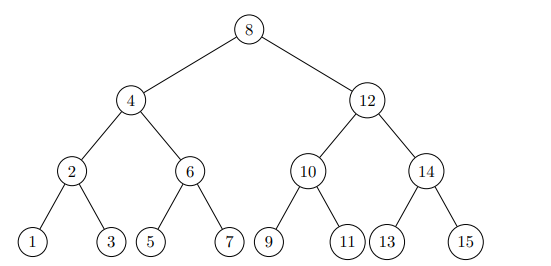
Exercise 13.1-1
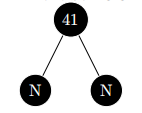
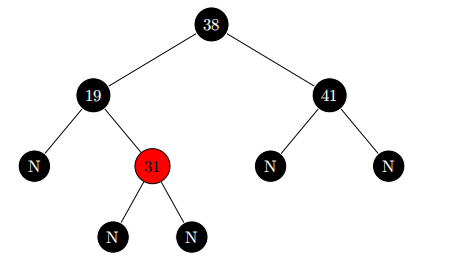
我们将NIL缩短为N,以便在文档中更容易显示。下图的黑高度为2。
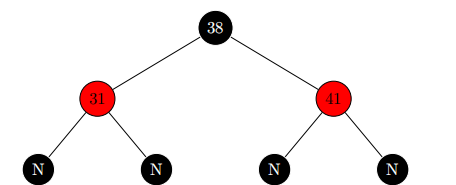
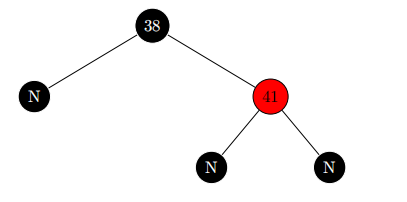
下图的黑高度为3。
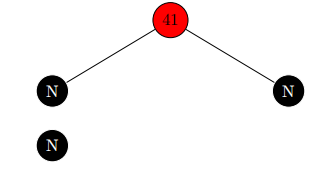
最后,下图的黑高度为4。
Exercise 13.1-2
如果插入的节点是红色的,那么它就不是红黑树,因为35是36的父结点,36也是红色的。如果插入的节点是黑色的,它也不能成为红黑树,因为从节点38到T.nil有两条路径包含不同数量的黑节点,违反了性质5。在下面的树图中,由于空间原因,省略了NIL节点。
Exercise 13.1-3
会的。没有引入红节点,所以仍然满足4。因为根结点在从根结点到叶结点的每一条路径上,而不是其他路径上。5会被满足,因为我们要改变黑节点数量的路径只有那些来自根结点的路径。所有这些都会增加1,所以它们都是相等的。由于没有新叶的引入,3是微不足道的保存。1也被简单地保留了下来,因为它只改变了一个节点,没有被改变成某种神秘的第三种颜色。
Exercise 13.1-4
可能的度数是0到5,取决于黑节点是否是根节点,以及它是否有一个或两个红色子节点,每个子节点有一个或两个黑色子节点。深度最多只能缩小1/2。
Exercise 13.1-5
假设我们有最长的简单路径(a1, a2,…as)和最短简单路径(b1, b2,…bt)。然后,根据性质5,我们知道它们有相等数量的黑节点。根据性质4,我们知道它们都不包含重复的红节点。这告诉我们最长路径上最多有
个节点是红色的。这意味着至少有
是黑色的,所以t≥d (s+1)因此,如果,通过矛盾的方式,我们有s > t*2,那么
是个矛盾。
Exercise 13.1-6![]()
在从根到叶的路径中,任意两个黑节点之间最多有一个红节点,所以这种树的最大高度是2k+1,从根到叶的每条路径都是红节点和黑节点交替出现。为了最大化内部节点,我们使树完整,总共有2^(2k+1)−1个内部节点。最小可能数量的内部节点来自于一个完全二叉树,其中每个节点都是黑色的。它有2^(k+1)−1个内部节点。
Exercise 13.1-7
因为每个红色节点需要有两个黑色的子节点,我们唯一的希望就是相对于我们的黑色内部节点的数量,得到大量的内部红色节点,就是让每个叶节点的父节点都是一个红色节点。如果树根是黑色,子结点是红色,子结点是红色,子结点都是叶子,那么比值就是2/3。没有比这更好的了因为随着树形变大,比值接近1/2。最小的比例是通过一个完整的树来实现的,它是平衡的,黑得像乌鸦的羽毛。例如,参见13.1-1解决方案中给出的最后一个树。
Exercise 13.2-1
![]()
参见RIGHT-ROTATE算法。
Exercise 13.2-2![]()
我们用归纳法进行。在只有一个节点的树中,根结点既没有左子结点也没有右子结点,所以旋转是无效的。假设有n≥0个节点的树恰好有n−1个旋转。设T是一个有n + 1个节点的二叉搜索树。如果T.root没有右子结点,那么根结点只能参与一次右旋转,而T的左子结点有n个顶点,所以它正好有n - 1次旋转,整个树总共有n个顶点。如果T.root没有左子节点,参数是相同的。最后,假设T.root有两个子树,让k表示左子树的节点数。然后根可以向左或向右旋转,对计数有贡献。根据归纳假设,T.left恰好有k−1个旋转,T.right恰好有n−k−1个旋转,所以总共有2+k−1+n−k−1 -1= n个可能的旋转,完成了证明。
Exercise 13.2-3
c的深度减少1,b的深度保持不变,a的深度增加1。
Exercise 13.2-4
考虑将任意n节点BT转换成一条右行链:设根和根的所有连续右子节点为链初始链的元素。对于链上节点的左子节点x,对x的父节点进行一次向右旋转将把该节点添加到链中,而不会从链中删除任何元素。因此,我们可以将任何BST转化为最多有n - 1个右旋的右链。设r1 r2…, rk为将某BST T1转化为右行链所需的旋转序列,设s1, s2,…, sm是将另一个BST T2转化为右向链所需的旋转序列。然后k < n, m < n,我们可以将T1转化为T2,通过执行序列r1, r2,…, rk,
,其中s'i是si的反向旋转。由于k+m < 2n,所需的旋转次数为O(n)。
Exercise 13.2-5
考虑T2的BST为
设T1为
那么,在T1中没有节点可以有效地调用右旋转。虽然可以把T2右转换成T1,但反过来是不可能的。
对于任何BST T,定义量f(T)为从根节点到该节点的简单路径中使用的左指针数量对所有节点的和。注意,每个节点的贡献是O(n)。因为只有n个节点,我们得到f(T) = O(n^2)同样,当我们调用右旋转(T,x)时,x的贡献减少1,而所有其他元素的贡献保持不变。由于f(T)是一个在每次右旋调用时正好减少1的量,并且从O(n^2)开始,并且永远不会变为负值,我们知道在BST上最多只能有O(n2)次右旋调用。
Exercise 13.3-1
如果我们选择将z的颜色设置为黑色那么我们就违反了红黑树的性质5。因为在z下,从根结点到叶结点的任何路径都会比到其他叶结点的路径多一个黑节点。
Exercise 13.3-2
Exercise 13.3-3
对于z是右子情况,我们附加每个节点的黑高度来得到
需要注意的是,虽然节点的黑深度可能会改变,但它们仍然是定义良好的,因此它们仍然满足红黑树的条件5。类似于当z是左子结点时的树。
Exercise 13.3-4
首先注意到,RB-INSERT-FIXUP只修改已经是红色的节点的子节点,因此我们永远不会修改设置为T.nil的子节点。我们只需要检查根节点的父节点是否从未被设置为红色。由于根节点和根节点的父节点自动为黑色,如果z的深度小于2,while循环将被中断。我们只修改z以上最多两层的节点颜色,所以我们需要担心的唯一情况是,如果z的深度为2。在本例中,我们冒险将根目录修改为红色,但这在第16行处理。当z更新时,它要么是根,要么是根的子节点。无论哪种方式,根节点和根节点的父节点仍然是黑色的,因此违反了while条件,因此不可能将T.nil修改为红色。
Exercise 13.3-5
假设我们只加上最后一个元素。然后,在调用RB-INSERT-FIXUP之前,我们知道它是红色的。在执行while循环的所有修复案例中,我们得到的结果树片段包含一个红色的非根节点。稍后在第16行中不会将该节点设置为黑色,因为它不是根节点。
Exercise 13.3-6![]()
我们需要从RB-INSERT中删除第8行并修改RB-INSERT- fixup。在RB-INSERT-FIXUP中的任何一点,我们只需要跟踪最多2个祖先:z.p和z.p.p。我们可以在log n时间内找到并存储这些节点,并在调用RB-INSERT-FIXUP期间使用它们。这不会改变RB-INSERT的运行时间。
Exercise 13.4-1
![]()
有两种方法可以离开RB-DELETE-FIXUP的while循环。首先,我们有x = T.root。在本例中,我们在第23行设置了x.color = BLACK。所以根结点一定是黑色的。另一种情况是,我们结束了while循环,因为我们有x.color == RED,但有x = T.root。这个规则情况下4,因为,我们设置x = T.root。在情形3中,我们没有将x设为红色,或者根本没有改变x,所以它不可能是最后一次运行。在情况2中,我们没有将任何新内容设置为红色,因此不会因此而退出while循环。在第1种情况下,我们将兄弟结点设置为黑色,并将其旋转到父结点的位置。因此,在这一步中不可能将根节点设置为红色,因为我们将唯一的节点设置为红色,然后在上面放置一个黑色节点。
Exercise 13.4-2
假设在RB-DELETE中x和x.p都是红色的。这只能发生在第9行的else-case中。因为我们是从红黑树中删除的,所以y.p的另一个子结点(在第14行调用RB-TRANSPLANT时成为x'的兄弟结点)必须是黑色的,所以x是x.p的唯一的子结点(是红色的)。立即违反了RB-DELETE-FIXUP(T,x)的while-loop条件,因此我们简单地设置x.color = black,恢复属性4。
Exercise 13.4-3
Exercise 13.4-4![]()
由于w有可能是T.nil,因此必须包含检查或修改w的任何RB-DELETE-FIXUP(T,x)行。然而,正如第317页所描述的,x永远不会是T.nil,所以我们不需要包含这些行。
Exercise 13.4-5
我们的计数将包括根(如果它是黑色的)。
情况1:前后每个子树的计数都是2
情况2:在两种情况下,子树α和β的计数都是1+count(c),其余子树的计数从2+count(c)到1+count(c)。其他子树计数的减少是通过x来处理的代表一个额外的黑色。
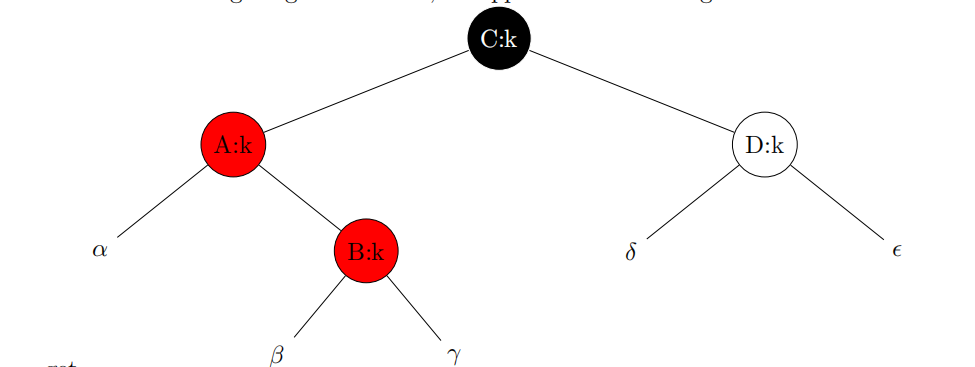
情况3:对和ζ的计数在前后都是2+count(c),对于所有其他子树,在前后都是1+count(c)
情况4:对于α和β,计数从1+count(c)变为2+count(c)。对于γ和δ,在前后都是1+count(c)+count(c ')。对于和ζ,在前后都是1+ count(c)。α和β计数的增加是因为前面的x表示一个额外的黑色。
Exercise 13.4-6
在情况一开始,我们把w设为x的兄弟结点,我们在第4行检查w.color == red,这意味着x和w的父元素不能是红色的。否则违反了性质4。因此,他们的担心是没有根据的。
Exercise 13.4-7
假设我们按照这个顺序插入元素3、2、1,那么,得到的树是这样的
然后,在删除最后添加的元素1之后,生成的树是

然而,在插入1之前的树是
这两棵红黑树明显不同






































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








