【算法解析】看懂树状数组

从问题入手

首先来看这样一种问题

单点修改&单点查询
时间限制：1秒　　内存限制：128MB
题目操作
给定一个由 $n$ 个元素组成的数组 $a$ ，要求进行 $t$ 次以下操作：

• 修改操作：输入 $x$ 和 $y$ ，将 $a_x$ 的值改为 $y$ 。
• 查询操作：输入 $x$ ，输出 $a_x$ 的值。

数据范围
$1\le n\le 10^5,1\le a_i\le 10^9$

这个问题 但凡会写定义 循环 输入 路障僵尸都能做 比较简单，就不用放代码了。最基础的C++入门类问题，c操作时用赋值操作a[x]=y;，q操作时用cout<<a[x];就可以了。

接下来看这种问题

区间查询
时间限制：1秒　　内存限制：128MB
题目描述
给定一个由 $n$ 个元素组成的数组 $a$ ，要求进行 $t$ 次查询操作，对于每次操作，给定两个数 $L$ 和 $R$ ，输出 $a_l+a_{l+1}+a_{l+2}+\cdots +a_{r-1}+a_r$ 的和。

数据范围
$1\le n\le 10^5,1\le a_i\le 10^9$

这个问题 前缀和暗自窃喜 没学过一脸懵逼 还是比较简单，只不过在$O(n)$的时间复杂度里进行区间查询涉及到了一种特定的算法前缀和。前缀和数组定义为$f[i]={\sum }_i^{j=1}a[j]$ 或 $f[i]=f[i-1]+a[i]$ （从$a_1$加到$a_i$的和）。建立数组时时间复杂度为$O(n)$，对于查询操作，输出f[r]-f[l-1]即 $l$ 到 $r$ 的区间和。

再来看这种问题

区间修改
时间限制：1秒　　内存限制：128MB
题目描述
给定一个由 $n$ 个元素组成的数组 $a$ ，要求进行 $t$ 次修改操作，对于每次操作，给定三个数 $L$ 、 $R$ 和 $x$ ，将 $a_L$ 至 $a_R$ 区间的元素加上 $x$ 。接下来进行 $q$ 次查询操作，每次操作给定一个数 $x$ ，输出 $a_x$ 的值。

数据范围
$1\le n\le 10^5,1\le a_i\le 10^9$

这个问题 差分党直接狂喜 新学者自认垃圾 与上面的题难度几乎相当。区别在于这次以区间修改和单点查询代替了区间查询。这就需要用到前缀和的逆操作兼好兄弟 差分来解决了。

差分数组定义为 $f[i]=a[i]-a[i-1]$ ，表示序列中当前位的元素与上一位元素的差。运用差分，对于此题的修改操作只需要f[l]+=x,f[r+1]-=x;即可。这是因为差分数组有个重要的特性：差分的前缀和等于原数组。同样的，在查询操作前求出差分数组的前缀和f[i]+=f[i-1]，面对查询就可以直接输出f[i]了。

如果只看前缀和系列，再延伸也只能是二维之类的了，解起来没啥区别。
但是这道题并不是

单点修改&区间查询
时间限制：1秒　　内存限制：128MB
题目描述
给定一个由 $n$ 个元素组成的数组 $a$ ，要求进行 $t$ 次修改或查询操作。对于每次修改操作，给定两个数$x$和$y$，将a[x]的值加上y。对于每次查询操作，给定两个数 $L$ 和 $R$ ，输出 $a_l+a_{l+1}+a_{l+2}+\cdots +a_{r-1}+a_r$ 的和。

数据范围
$1\le n\le 10^5,1\le a_i\le 10^9$

可以看到，这道题在前缀和的基础上加了单点修改的操作。对于修改操作，如果没有区间求和的要求，我们可以直接用a[x]+=y;来解决。但是由于前缀和的串联性，为了维护它，一旦修改就必须修改往后的所有前缀和，而这就需要$o(n^2)$的时间复杂度，把前缀和的速度优势完全抵消掉了。

接下来让我们再用一道题破了拆分

区间修改&单点查询
时间限制：1秒　　内存限制：128MB
题目描述
给定一个由 $n$ 个元素组成的数组 $a$ ，要求进行 $t$ 次修改或查询操作。对于每次修改操作，给定三个数$l$、$r$和$x$，将a[l]~a[r]区间内的数值加上$x$。对于每次查询操作，给定一个数 $x$，输出a[x]的值。

数据范围
$1\le n\le 10^5,1\le a_i\le 10^9$

熟悉的题目，熟悉的感觉。差分在区间修改这方面的优势，由于随时查询或修改的 恶心 特性，被彻彻底底地抵消掉了，每次查询都需要求一遍前缀和，时间复杂度也是$O(n^2)$。

这两种问题一定是不能再这么解了。如果我告诉所有正在苦恼的读者，树状数组就是解决这类更复杂问题的方法之一，为了保护你不受这类题的困扰，你可以学习树状数组来简单抵抗一下。你应该会看下去吧。

基本概念

树状数组是一种有趣的数据结构（线段树退化版）。

将输入的序列用正常的一维数组存起来。
现在把它们想象成叶子节点。
两两合并，创造新的节点向上延伸。
直到有一层只剩下一个节点时，它就成为一棵二叉树。
把二叉树向右对齐。
好了，就到这里。
（放个图你就明白了）

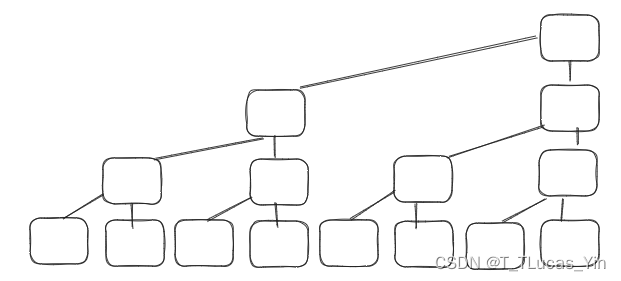
^{图：一棵右对齐的二叉树}
接下来，让我们按照树的竖列看，只留下每一列最顶端的点和叶子节点。
现在，把其他多余的节点都删掉。
然后，让留下的顶端节点直接连接到曾经它的儿子下面的点

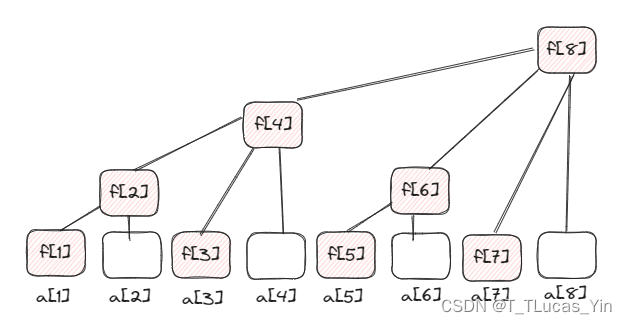
^{图：a[i]表示输入的第i个元素，f[i]表示树状数组的第i个元素}
现在树的每一列存在两种节点，一个是这一列顶端的点，一个是叶子节点。
树的叶子节点代表输入的序列，存在数组$a$里。
可以看到我把顶端的节点都涂了红色阴影，并标上了序号，表示它们依次存在另一个数组$f$的对应下标上。

使用方法

数组$f$代表的就是树状数组。根据上图树上的边可以看出$f$数组中存储的内容，如
f[1]=a[1]，f[2]=a[1]+a[2]，f[4]=a[1]+a[2]+a[3]+a[4]，f[6]=a[5]+a[6]，f[7]=a[7]。
看起来杂乱无章，但$f$数组存储的内容其实和二进制有很大关系。请看下表：

序号	二进制表示	存储序列中的元素数量
1	0001	1
2	0010	2
3	0011	1
4	0100	3
5	0101	1
…	…	…
8	1000	4

可以看出，如序号的因数最大包含$2^k$，$f$数组的这个位置就存储了$k+1$个元素的和。更直白一点：序号的二进制表示中第一个“$1$”在第几位，这个位置就是几个元素相加！

求出二进制序号中第一个1的位置不需要用循环一次次试，而可以用简单的计算得到。先求出数字的反码，然后加1，得到补码，也就是原数的负数。在原数和补码之间进行与运算，结果就是第一个1的位置。写成语句就是x&-x;。我们把这种操作称为lowbit。可以得知，原序列中的第$x$个元素，只在树状数组中的$x+nlowbit(i)$位置出现。

代码实现

接下来我们就看一下树状数组的一些基本操作

lowbit

非常简单的代码即可。时间复杂度$O(1)$

int lowbit(int k){
	return k&-k;
}

单点修改

如果要改变原序列中的一个数，就要改变在树状数组中所有包含这个数的元素。而这些位置就是当前位置$i$依次加上lowbit(i)。对于建树的操作，我们也可以看成输入数据后，将树状数组中的每一个元素的值都改变，就不需要单独思考了。时间复杂度$O(lo{g}_{2}n)$

void update(int x,int y){//将a[x]增加y
	for(int i=x;i<=n;i+=lowbit(i)) f[i]+=y;
}

区间查询

按照前缀和中的思想，求一个区间的和可以用两个位置到1的区间和相减，得到中间的部分区间。在树状数组中也同理。求从1到$x$位的和，其顺序与修改操作相反，就是从c[x]开始，下标依次减去lowbit(i)，一直到1，得到$a[1]+a[2]+\cdots +a[x-1]+a[x]$。
时间复杂度$O(lo{g}_{2}n)$。

long long getsum(int x){//求和记得用long long
	long long sum=0;
	for(int i=x;i;i-=lowbit(i)) sum+=f[i];
	return sum;
}

区间修改

对于区间修改的操作，也可以使用类似前缀和的思想。在树状数组中，依旧存储一样的数据，只是在要修改的区间中，给l~n加上$x$后，还需要将r+1~n减去$x$。

void update(int l,int r,int k){
	for(int i=l;i<=n;i+=lowbit(i)) f[i]+=k;
	for(int i=r+1;i<=n;i+=lowbit(i)) f[i]-=k;
}

例题解析

好了。到这里为止，与上面的两道难题相关的所有代码也已经给出了。利用这些已知关于树状数组的代码，我们可以在$O(nlo{g}_{2}n)$的时间复杂度下通过难题。虽然不如前缀和和差分，但足够使用了。恭喜你，我们有了应对这种刁钻题的实力。下面给出其中一道题的代码。

单点修改&区间查询
时间限制：1秒　　内存限制：128MB
题目描述
给定一个由 $n$ 个元素组成的数组 $a$ ，要求进行 $t$ 次修改或查询操作。对于每次修改操作，给定两个数$x$和$y$，将a[x]的值加上y。对于每次查询操作，给定两个数 $L$ 和 $R$ ，输出 $a_l+a_{l+1}+a_{l+2}+\cdots +a_{r-1}+a_r$ 的和。

数据范围
$1\le n\le 10^5,1\le a_i\le 10^9$

AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,t,l,r,x,y,a[100005],f[100005];
int lowbit(int k){ return k&-k; }
void update(int x,int y){//将a[x]增加y
	for(int i=x;i<=n;i+=lowbit(i)) f[i]+=y;
}
long long getsum(int x){//求和记得用long long
	long long sum=0;
	for(int i=x;i;i-=lowbit(i)) sum+=f[i];
	return sum;
}
int main(){
	cin>>n>>t;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		update(i,a[i]);
	}
	while(t--){
		char c;
		cin>>c;
		if(c=='1'){
			cin>>x>>y;
			update(x,y);
		}
		if(c=='2'){
			cin>>l>>r>>x;
			cout<<getsum(r)-getsum(l-1)<<"\n";
		}
	}
	return 0;
}

至于另一道题，我就懒得放代码了 就留给大家自行思考了。

---