Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
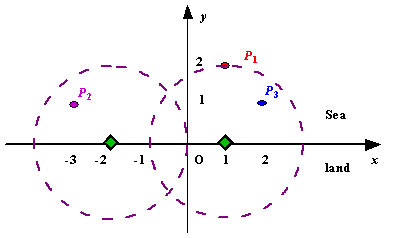
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
先用结构体将岛屿保存并按x大小排序,然后一个一个取,取出来一个就可以与其距离为d的且在x轴上的点的横坐标,这个计算出来的值就是现在假定了一个圆心在该位置,再接着继续取点,取出来一个计算一次圆心,如果新的圆心在目前的这个圆心的左边,那么更新当前圆心为新计算的这个圆心,因为这样的话就能保证之前那个点和现在这个点都在圆里。如果新的圆心在目前这个圆心的后面,那么就计算这个点和当前圆心的距离,如果小于半径d,那么就是虚惊一场,如果大于那么就要一个新的圆来包含它了,这是计数cnt就加一,全部算一遍,答案就出来了
代码
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
struct node
{
int x;
int y;
}land[1005];
bool cmp(node a,node b)
{
if(a.x!=b.x)
return a.x<b.x;
return a.y>b.y;
}
int main()
{
ios::sync_with_stdio(false);
int n;
int maxy;
long long d;
int cas=1;
while(cin>>n>>d)
{
maxy=0;
if(n==0&&d==0)
break;
bool suc=true;
for(int i=0;i<n;i++)
{
cin>>land[i].x>>land[i].y;
maxy=max(maxy,land[i].y); //记录离岸最远的岛屿的垂直距离
}
sort(land,land+n,cmp);
int cnt=1;
int i=1;
if(maxy>d)
{
cout<<"Case "<<cas++<<": "<<-1<<endl; //提前判断一下,如果有哪个岛屿是无论如何都不能被雷达侦测的,那就输出-1
continue;
}
double r=land[0].x+sqrt(d*d-land[0].y*land[0].y);
while(i<n)
{
double rr=land[i].x+sqrt(d*d-land[i].y*land[i].y);
if(rr<r)
{
r=rr;
i++;
continue;
}
if(sqrt((land[i].x-r)*(land[i].x-r)+land[i].y*land[i].y)>d)
{
cnt++;
r=rr;
}
i++;
}
cout<<"Case "<<cas++<<": "<<cnt<<endl;
}
return 0;
}





















 1108
1108

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








