【笔记】郑州大学ACM实验室寒假新生培训之 排列组合与容斥

》》b站视频链接《《

OP

\

组合数和排列数

对于组合数（C）和排列数（A\P），从n个元素中选取m个，有

$$\begin{gathered} C_n^m=\frac{n!}{m!(n-m)!} \\ {A}_n^m=C_n^m\cdot m!=\frac{n!}{(n-m)!} \end{gathered}$$

关于组合数，以下推论均成立

$$\begin{gathered} C_n^m=\frac{n}{m}{C}_{n-1}^{m-1} \\ {C}_n^m=C_n^{n-m} \\ {C}_n^m=C_{n-1}^{m-1}+C_{n-1}^m \end{gathered}$$

组合数与杨辉三角

杨辉三角形如

$$\begin{gathered} 1 \\ 11 \\ 121 \\ 1331 \\ 14641 \end{gathered}$$

不难发现，其中第 n 行的第 m 个数（从0开始）恰好为 $C_n^m$ 的值；

Lucas定理

求取 $C_n^m\%p$ 时，若 m , n 满足

$$\begin{gathered} n=n_k{p}^k+n_{k-1}{p}^{k-1}+...+n_{1}p+n_0 \\ m=m_k{p}^k+m_{k-1}{p}^{k-1}+...+m_{1}p+m_0 \end{gathered}$$

则有

$$C_n^m\equiv \prod _{i=0}^k{C}_{n_i}^{m_i}(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

也可以用递归表示：

$$C_n^m=lucas(n,m)\equiv C_{n\%p}^{m\%p}\cdot lucas(\frac{n}{p},\frac{m}{p})(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

代码如下

//求C_a^b
ll comp(ll a,ll b,ll m){
    if(a<b) return 0;
    if(a==b) return 1;
    if(b>a-b) b=a-b;
    ll ans=1,ca=1,cb=1;
    for(int i=0;i<b;i++){
        ca=ca*(a-i)%m;
        cb=cb*(b-i)%m;
    }
    ans=ca*qm(cb,m-2)%m;
    return ans;
}

ll lucas(ll a,ll b,ll m){
    ll ans=1;
    while(a&&b){
        ans=(ans*comp(a%m,b%m,m))%m;
        a/=m;
        b/=m;
    }
    return ans;
}

容斥原理

在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

摘自百科词条

公式如下，亦摘自上链

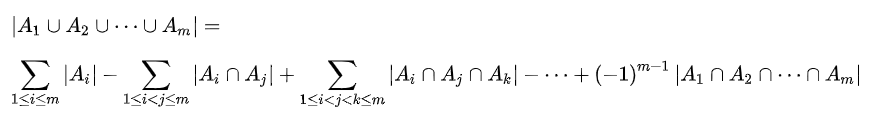
简单来说，容斥原理是一个不断修正偏差的过程，每一次都是在修正上一次所产生的重复 \ 遗漏；

错位排序

求 n 的全排列中，1~n 的每个数都不在初始位置的方案数；

n 的全排列有 $n!$ 个，减去其中至少有一个数在正确位置的情况 $C_n^1(n-1)!$ ，刚刚减去的部分重复减去了至少两个数在正确位置的情况，应再加上 $C_n^2(n-2)!$ ，刚刚加上的部分又重复加上了至少三个数在正确位置的情况，应再减去 $C_n^3(n-3)!$ …

以此类推，n 的错排有 $D_n={\sum }_{i=0}^n{C}_n^i(n-i)!(-1{)}^i$ ；
与此同时，错排有递推式 $D_n=(n-1)(D_{n-1}+D_{n-2})$ ；
在查阅这篇文章中，找到了错排的估计公式 $D_n=\lfloor \frac{n!}{e}+\frac{1}{2}\rfloor$ ;

m球n盒问题

1. 球相同，盒可空
   我们可以假设 m 个球和 n-1 个隔板共同排序，第一个隔板前面的在第一个盒，第二个隔板与第一个隔板之间的在第二个盒…第 n-1 个隔板和第 n-2 个隔板之间的在第 n-1 个盒，第 n-1 个隔板之后的在第 n 个盒；
   由于 m 个球相同，那么 n-1 个隔板所在位置不同的情况有 $C_{m+n-1}^{n-1}$ ，即在所有位置中选出 n-1 个位置的选法；
2. 球相同，盒不空
   我们可以假设在 m 个球之间的 m-1 个空中插入 n-1 个隔板（每空至多一个隔板），那么 n-1 个隔板所在位置不同的情况有 $C_{m-1}^{n-1}$ ，即在所有位置中选出 n-1 个位置的选法；
3. 球不同，盒可空
   每一个球都有 n 种选法，即 $n^m$ ；
4. 球不同，盒不空
   容斥：全集减非法集；
   全集即为 $n^m$ ，其中至少有一个盒子空的情况有 $C_n^1(n-1{)}^m$ ，至少有两个盒子空的情况有 $C_n^2(n-2{)}^m$ ，由容斥原理，不同的情况有 ${\sum }_{i=1}^n{C}_n^i(n-i{)}^m(-1{)}^i$ 种；

多重集的r-组合数

截图自清华大学出版社《离散数学（第三版）》

ED

\