[硫化铂]未来

未来

题目概述

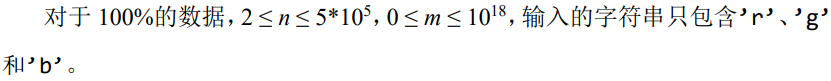
题解

首先，我们考虑用某种线性变化转化一下我们的这个变化。
我们不妨定义$r,b,g$在模三的剩余系下分别为$0,1,2$，那么如果我们每次转移是让$x^{\prime }=2(x+y)\%3$的话，显然就满足我们每次操作的条件了。
如果我们连续对一个数进行$m$次操作的话，我们发现，我们对$a_i$进行第$j$次操作时，是需要考虑它下一个数$a_{i+1}$进行$j-1$次操作的答案的。
我们定义$f(i,j)$表示对$a_i$进行$j$次操作得到的答案，显然有转移式
$$f(i,j)=2(f(i,j-1)+f(i+1,j-1))\%3$$发现这个长得很像杨辉三角的形式，那么我们可以知道将整个函数展开后可以得到，$f(i,m)=2^m{\sum }_{j=0}^m\left(\genfrac{}{}{0ex}{}{m}{j}\right)a_{(i+j)\%n}$
也就是说$a_j$对$a_i$贡献的系数为${\sum }_{k=0}^m[k\equiv i-j\mathrm{m}\mathrm{o}\mathrm{d}n]\left(\genfrac{}{}{0ex}{}{m}{k}\right)$
显然，这东西只与$i-j$的大小有关，记$f_i={\sum }_{k=0}^{\lfloor \frac{m-i}{n}\rfloor }\left(\genfrac{}{}{0ex}{}{m}{nk+i}\right)$，我们需要算的显然只有这东西。

如果暴力算的话肯定承受不住我们$m⩽10^{18}$的范围，但我们的模数是$3$呀，考虑Lucas定理，这样我们可以将$m$转化成三进制数后进行计算，每个位上的组合数乘起来。
我们定义$d{p}_{i,j}$表示考虑到第$i$位，我们已经枚举过的位置对于模$n$的余数为$j$的组合数之和，记$m$三进制的第$i$位为$a_i$，显然有转移式，
$$d{p}_{i,j}=\sum _{k=0}^{a_i}\left(\genfrac{}{}{0ex}{}{a_i}{k}\right)d{p}_{i-1,(j-k\cdot 3^i)\%n}$$显然，就是直接枚举我们这一位填的数为多少。
按常理来说还要保证我们填出来的数不能大于$m$，但是我们填的数如果有一位比$m$这位大，贡献就为$0$了，所以有贡献的数总和必定不超过$m$，没必要考虑舔出来大于$m$的情况。
最后我们的$d{p}_{len,i}$就是我们的$f_i$。
有了$f_i$，我们对于原字符串随便做一个多项式乘法就能得到我们的答案串了。

时间复杂度$O\left(n({\log }_{3}m+\log n)\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 500005
#define MAXM 2000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int mod=1e5+3;
const int inv2=499122177;
const int jzm=2333;
const int zero=2000;
const int n1=2000;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,a[MAXN],sta[MAXN],stak,pw3[MAXN],dp[45][MAXN],C[5][5];
int F[MAXM],G[MAXM],rev[MAXM];char str[MAXN];LL m;
void NTT(int *A,const int lim,const int typ){
	for(int i=0;i<lim;i++)if(rev[i]<i)swap(A[i],A[rev[i]]);
	for(int mid=1;mid<lim;mid<<=1){
		const int W=qkpow(typ^1?ivG:orG,(mo-1)/(mid<<1),mo);
		for(int i=mid<<1,j=0;j<lim;j+=i)
			for(int k=j,Wn=1;k<j+mid;k++,Wn=1ll*W*Wn%mo){
				const int x=A[k],y=1ll*Wn*A[k+mid]%mo;
				A[k]=add(x,y,mo);A[k+mid]=add(x,mo-y,mo);
			}
	}
	if(typ^-1)return ;int tmp=qkpow(lim,mo-2,mo);
	for(int i=0;i<lim;i++)A[i]=1ll*tmp*A[i]%mo;
}
signed main(){
	freopen("future.in","r",stdin);
	freopen("future.out","w",stdout);
	for(int i=0;i<4;i++){
		C[i][0]=C[i][i]=1;
		for(int j=1;j<i;j++)
			C[i][j]=(C[i-1][j-1]+C[i-1][j])%3;
	}
	read(n);read(m);scanf("\n%s",str+1);int tmp=qkpow(2,m%2,3);
	for(int i=1;i<=n;i++)a[i]=(str[i]=='r')?0:((str[i]=='g')?1:2);
	while(m)sta[++stak]=m%3,m/=3;int now=0,las=1;dp[now][0]=1;
	pw3[0]=1;for(int i=1;i<=stak;i++)pw3[i]=3ll*pw3[i-1]%n;
	for(int i=stak;i>0;i--){
		swap(now,las);
		for(int j=0;j<n;j++)if(dp[las][j]){
			for(int k=0;k<=sta[i];k++)
				(dp[now][(j+k*pw3[i-1])%n]+=C[sta[i]][k]*dp[las][j])%=3;
			dp[las][j]=0;		
		} 
	}
	int lim=1,len=0;while(lim<(n<<1))lim<<=1,len++;
	for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<len-1);
	for(int i=1;i<=n;i++)F[i]=a[i];
	for(int i=0;i<n;i++)G[n-i]=dp[now][i];
	NTT(F,lim,1);NTT(G,lim,1);for(int i=0;i<lim;i++)F[i]=1ll*F[i]*G[i]%mo;NTT(F,lim,-1);
	for(int i=n;i<lim;i++)F[i%n]+=F[i];
	for(int i=0;i<n;i++)F[i]=1ll*tmp*F[i]%3;
	for(int i=1;i<=n;i++)putchar(!F[i%n]?'r':(F[i%n]==1?'g':'b'));
	puts("");
	return 0;
}

谢谢！！！