刷题小结---动态规划篇

前言

最近刷题总是寄在动态规划的问题上，单独开个篇记录一下。

遇到动态规划的题不要怕，也不要用固有思路去套，关键在于对问题的细分，从而将复杂问题简单化，我个人觉得动态规划和递推非常像，后面的值的计算需要用到前面算出来的值。

华为机试从牛客题库来看好像非常喜欢考察字符串处理和动态规划，而且经常放一起，所以动态规划是绕不开的一道坎，必须硬啃下来。

---

一、理论

1、基本概念

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

2、基本思想与策略

基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

与分治法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

3、适用的情况

能采用动态规划求解的问题的一般要具有3个性质：

(1)最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

(2)无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

(3)有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

4、求解的基本步骤

动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。如图所示。动态规划的设计都有着一定的模式，一般要经历以下几个步骤。

初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态

(1)划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

(2)确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。

(3)确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

(4)寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

一般，只要解决问题的阶段、状态和状态转移决策确定了，就可以写出状态转移方程（包括边界条件）。

实际应用中可以按以下几个简化的步骤进行设计：

（1）分析最优解的性质，并刻画其结构特征。

（2）递归的定义最优解。

（3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值

（4）根据计算最优值时得到的信息，构造问题的最优解

5、算法实现的说明

动态规划的主要难点在于理论上的设计，也就是上面4个步骤的确定，一旦设计完成，实现部分就会非常简单。

使用动态规划求解问题，最重要的就是确定动态规划三要素：

（1）问题的阶段

（2）每个阶段的状态

（3）从前一个阶段转化到后一个阶段之间的递推关系。

递推关系必须是从次小的问题开始到较大的问题之间的转化，从这个角度来说，动态规划往往可以用递归程序来实现，不过因为递推可以充分利用前面保存的子问题的解来减少重复计算，所以对于大规模问题来说，有递归不可比拟的优势，这也是动态规划算法的核心之处。

确定了动态规划的这三要素，整个求解过程就可以用一个最优决策表来描述，最优决策表是一个二维表，其中行表示决策的阶段，列表示问题状态，表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，从1行1列开始，以行或者列优先的顺序，依次填写表格，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。

f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}

6.常见问题：

只要吃透下面的这些基础问题，基本上难度一般的动态规划问题都可以有自己的思路了。

最长递增子序列（不连续）

*连续的子串就更简单了，简单写一下关键代码：

dp[1] = 1;
int max = 1;
for(int i=2;i<=n;i++){
	if(a[i-2] < a[i-1]){
    	dp[i] = dp[i-1] + 1;
    	max=Math.max(max,dp[i]);//统计整个过程中产生的最长的子串长度
	}else{
		//一旦相邻元素之间不递增，则累积的最长子串长度归1
        dp[i] = 1;
    }
}
System.out.print(max);

---

下面是不连续的子序列

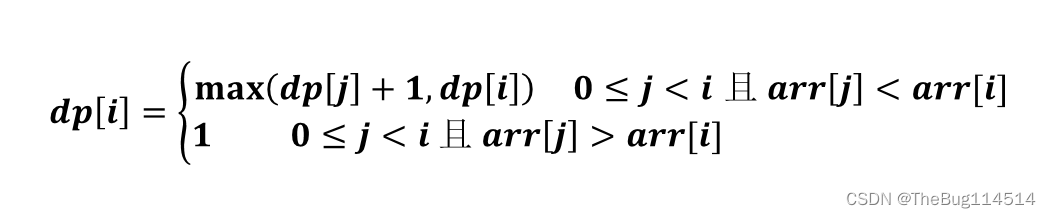
dp[i]表示以第i个为末尾的最长递增子序列的长度，因为不连续所以要设置双重循环，不再是连续地比较i与i-1的大小，而是要对于每一个数都要看它后面有没有一个比它更大的数可以构成更长的子序列；

也可以换种说法：对于每一个数 i ，都要看它是否能和它前面的从0到 i-1的数（记为 j ）构成更长的子序列，若能则要更新dp[i]的值，使dp[i] = dp[j] + 1。

class LIS 
{ 
    /* 动态规划解法 */
    static int lis(int arr[],int n) 
    { 
        int dp[] = new int[n]; 
        int i,j,max = 0; 
 
        /* 初始化 dp[] 数组中的每一个元素为 1 */
        for ( i = 0; i < n; i++ ){ 
            dp[i] = 1; 
        }
 
        /* 自底向上计算每一个问题的最优解*/
        for( i = 1; i < n; i++ ){ 
            for( j = 0; j < i; j++ ){  
                if ( arr[i] > arr[j] && dp[i] < dp[j] + 1){
                    dp[i] = dp[j] + 1;//也可把条件里的判断拿出来，写成 dp[i] = Math.max(dp[i],dp[j]+1)
                } 
            }
        }
 
        /* 遍历 dp 数组，找出最大值并返回 */
        for( i = 0; i < n; i++ ){ 
            if ( max < dp[i] ){ 
                max = dp[i]; 
            }
        }
        return max; 
    } 
}

最长公共子串

---

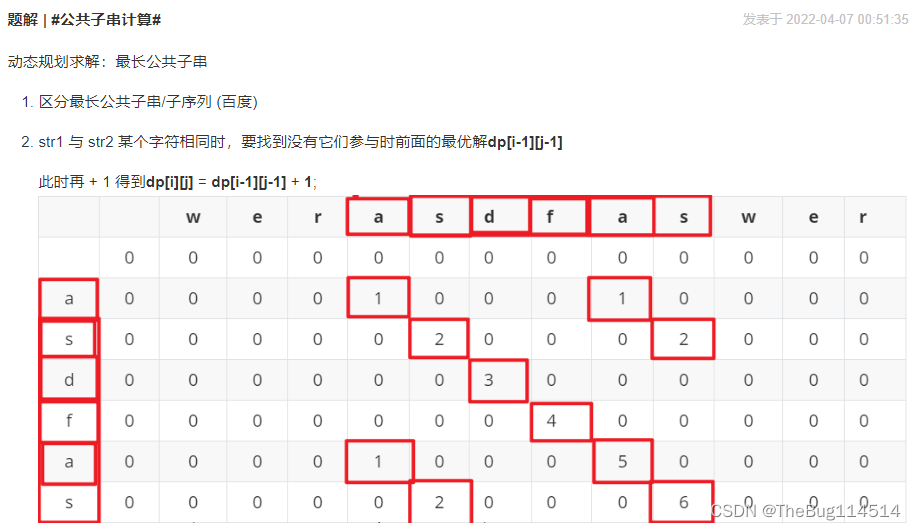
定义dp[i][j]表示s1的前i个字符与s2的前j个字符的末尾公共子串的最大长度，再定义一个变量max记录整个过程中产生的dp的最大值。

为什么要这么定义？一开始我的思路是定义为s1的前i个字符与s2的前j个字符的最大公共子串，想一步到位，但是这样定义带来的问题是，dp[i][j]很难与dp[i-1][j-1]或者dp[i-1][j]、dp[i][j-1]产生什么关联，因为我不知道dp[i-1][j-1]的最大公共子串是不是在末尾，如果在末尾那就很好办，比较s1的第i个字符与s2的第j个字符是否相同，若相同则最大子串长度+1。但是如果不在末尾呢，我比较这两个字符就没有任何意义，无法与前面的dp值产生任何互动。这一点让我很头疼，不得不看题解。

而像题解这么定义，相对于不是用dp直接记录s1的前i个字符与s2的前j个字符的最大公共子串，而是在记录整个过程中扫描到的所有公共子串的长度，然后我们只需要从中选出最大的那个数就是最大公共子串长度。

这一点和上面求最长递增子序列的思想其实是一样的。动态规划问题往往想一步到位是不行的，常常需要仔细思考如何设定dp[i][j]的含义。

---

字符串的编辑距离

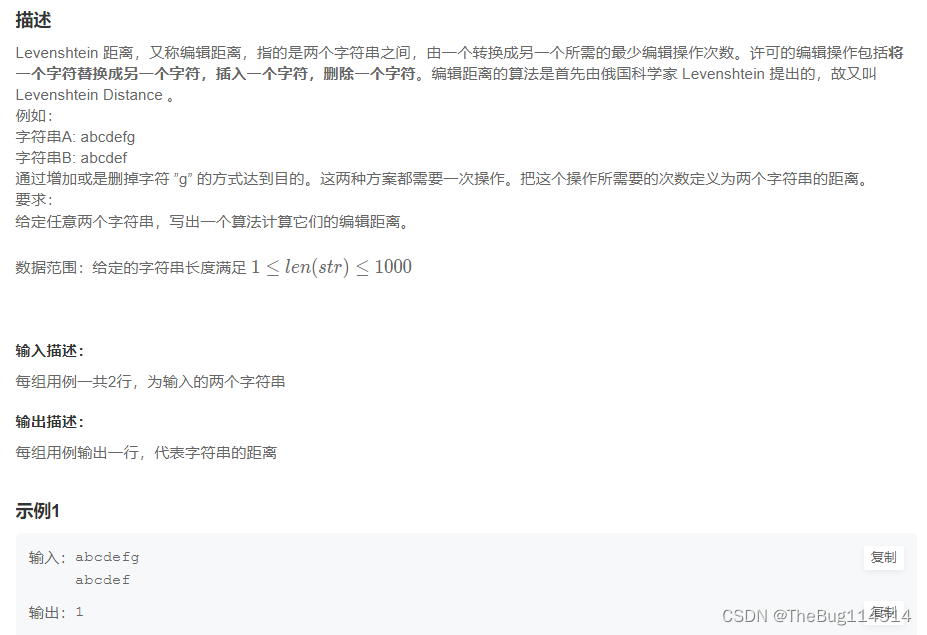
这个问题就可以一步到位，直接定义dp[i][j]表示s1的前i个字符与s2的前j个字符的编辑距离。

那么递推关系就是，如果第i个字符等于第j个字符，则dp[i][j] = dp[i-1][j-1]即不需要改动任何字符，编辑距离保持不变；

若i与j字符不相等，则有几种情况：改变一个字符、删除一个字符、添加一个字符，这几种操作都要使编辑距离+1。如果i与j前面的字符是对齐的情况，如abcd和abce这种，则dp[i][j]=dp[i-1][j-1]+1；如果是错开一位对齐的情况，如abcd和abc这种情况，则需要dp[i][j]=dp[i-1][j]+1或者dp[i][j]=dp[i][j-1]+1。

编辑距离显然是要求两个字符串间的“差距”的最小值（就是说abc到abcd只需要加上一个d，而不是a->b,b->c,c->d再在最前面加a），那么自然dp[i][j]就要取dp[i-1][j-1]+1、dp[i][j]=dp[i-1][j]+1、dp[i][j]=dp[i][j-1]+1三者中的最小值。

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        String s1 = in.nextLine();
        String s2 = in.nextLine();
        int[][] dp = new int[s1.length() + 1][s2.length() + 1];
        //前i与前j个字符的编辑距离
        //边界初始化
        for (int i = 1; i <= s1.length(); i++) {
            if (s1.substring(0, i).contains(s2.charAt(0) + "")) {
                dp[i][1] = i - 1;
            } else {
                dp[i][1] = i;
            }
        }
        for (int j = 1; j <= s2.length(); j++) {
            if (s2.substring(0, j).contains(s1.charAt(0) + "")) {
                dp[1][j] = j - 1;
            } else {
                dp[1][j] = j;
            }
        }
        //递推
        for (int i = 2; i <= s1.length(); i++) {
            for (int j = 2; j <= s2.length(); j++) {
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    dp[i][j]= dp[i-1][j-1];
                } else {
                    dp[i][j] = Math.min(dp[i-1][j]+1,dp[i][j-1]+1);
                    dp[i][j]= Math.min(dp[i][j],dp[i-1][j-1]+1);
                }
            }
        }
        System.out.print(dp[s1.length()][s2.length()]);
    }
}

数字翻译成字符串

---

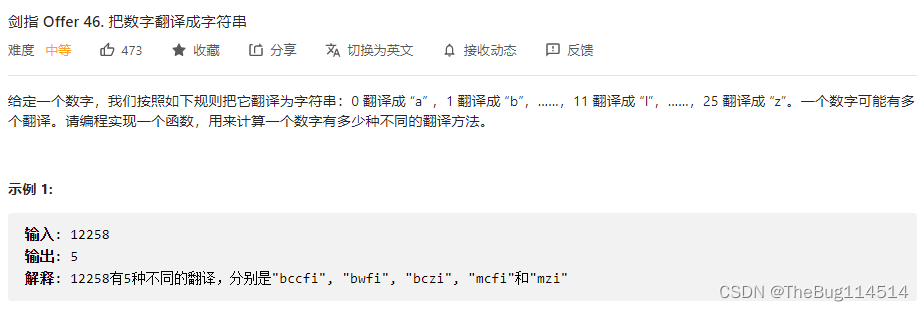
需要注意的是，对于两位数可以有两种翻译方法，此处有些类似“只能一步或两步爬楼梯”的问题，所以递推是dp[i]=dp[i-1]+dp[i-2]

public int translateNum(int num) {
        String s = num+"";
        int[] dp = new int[s.length()+1];
        //前i个数字的翻译方法
        dp[1] = 1;dp[0]=1;
        for(int i=2; i<=s.length();i++){
            if(Integer.parseInt(s.substring(i-2,i)) <= 25 && Integer.parseInt(s.substring(i-2,i)) >= 10){
                dp[i] = dp[i-1] + dp[i-2];
            }else{
                dp[i] = dp[i-1];
            }
        }
        return dp[s.length()];
    }

最长回文子串（对称子串）

---

解题思路：

对于最值问题，往往可以采用动态规划思想降低时间复杂度和状态压缩，采用空间换时间的思想

• 算法流程：

• 确定状态：对比的两个字符索引起始和终止索引位置

• 定义 dp 数组：字符串s的 i 到 j 索引位置的字符组成的子串是否为回文子串

• 状态转移: 如果左右两字符相等, 同时[l+1…r-1]范围内的字符是回文子串, 则 [l…r] 也是回文子串

状态转移的同时，不断更新对比的子串长度，最终确定最长回文子串的长度

注意对称子串中心可能是一个字符也可能是两个字符，但是只需要让左右字符相同且相差小于等于2时就认为其是对称子串

    public static int validLen(String s) {
        int len = s.length();
        // 状态：对比的两个字符索引起始和终止索引位置
        // 定义: 字符串s的i到j字符组成的子串是否为回文子串
        boolean[][] dp = new boolean[len][len];
        int res = 0;
        // base case
        for(int i = 0; i < len; i++) {
            dp[i][i] = true;
        }
 
        for(int r = 1; r < len; r++) {
            for(int l = 0; l < r; l++) {
                // 状态转移：如果左右两字符相等,同时[l+1...r-1]范围内的字符是回文子串
                // 则 [l...r] 也是回文子串
                if(s.charAt(l) == s.charAt(r) && (r-l <= 2 || dp[l+1][r-1])) {
                    dp[l][r] = true;
                    // 不断更新最大长度
                    res = Math.max(res, r - l + 1);
                }
            }
        }
        return res;
    }

背包问题

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

---

对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有两个方向推出来dp[i][j]，

不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)

放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagsize = 4;
        testweightbagproblem(weight, value, bagsize);
    }

    public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
        int wlen = weight.length, value0 = 0;
        //定义dp数组：dp[i][j]表示背包容量为j时，前i个物品能获得的最大价值
        int[][] dp = new int[wlen + 1][bagsize + 1];
        //初始化：背包容量为0时，能获得的价值都为0
        for (int i = 0; i <= wlen; i++){
            dp[i][0] = value0;
        }
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 1; i <= wlen; i++){
            for (int j = 1; j <= bagsize; j++){
                if (j < weight[i - 1]){
                    dp[i][j] = dp[i - 1][j];
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
                }
            }
        }
        //打印dp数组
        for (int i = 0; i <= wlen; i++){
            for (int j = 0; j <= bagsize; j++){
                System.out.print(dp[i][j] + " ");
            }
            System.out.print("\n");
        }
    }

连续子数组最大和

---

此题我们定义dp[i]表示以第i个数结尾的连续子数组的最大和。

不难发现，如果dp[i-1] < 0，则会对后面的累加起副作用，因此舍弃前面的累加，令dp[i]=nums[i-1];若dp[i-1] >= 0，则需要加上前面的数，因此dp[i] = dp[i-1]+nums[i-1]。
最后只需要找出dp中的最大值即可。

其实此处还能优化掉dp数组，只用两个变量以O(1)的复杂度实现，但是此处使用dp数组更易理解一些。

public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length+1];
        if(nums.length == 1)return nums[0];
        
        dp[1] = nums[0];
        for(int i=2; i<dp.length; i++){
            if(dp[i-1] < 0){
                dp[i] = nums[i-1];
            }else{
                dp[i] = dp[i-1] + nums[i-1];
            }
        }
        
        int max = dp[1];
        for(int i=2;i<dp.length;i++){
            max = Math.max(dp[i],max);
        }
        return max;
    }

股票最大盈利

1

打家劫舍

---

确定dp数组（dp table）以及下标的含义：
dp[i]：考虑前i间房屋，最多可以偷窃的金额为dp[i]。

确定递推公式：
决定dp[i]的因素就是第i房间偷还是不偷。

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出 下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。

如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

public int rob(int[] nums) {
        int[] dp = new int[nums.length+1];
        //前i个房子的最大收益
        dp[1] = nums[0];
        if(nums.length==1)return nums[0];
        dp[2] = Math.max(nums[0], nums[1]);
        if(nums.length==2)return dp[2];

        for(int i=3;i<=nums.length;i++){
            dp[i] = Math.max(dp[i-2] + nums[i-1], dp[i-1]);
        }
        return dp[nums.length];
    }

---

正则表达式匹配

---

二、题解

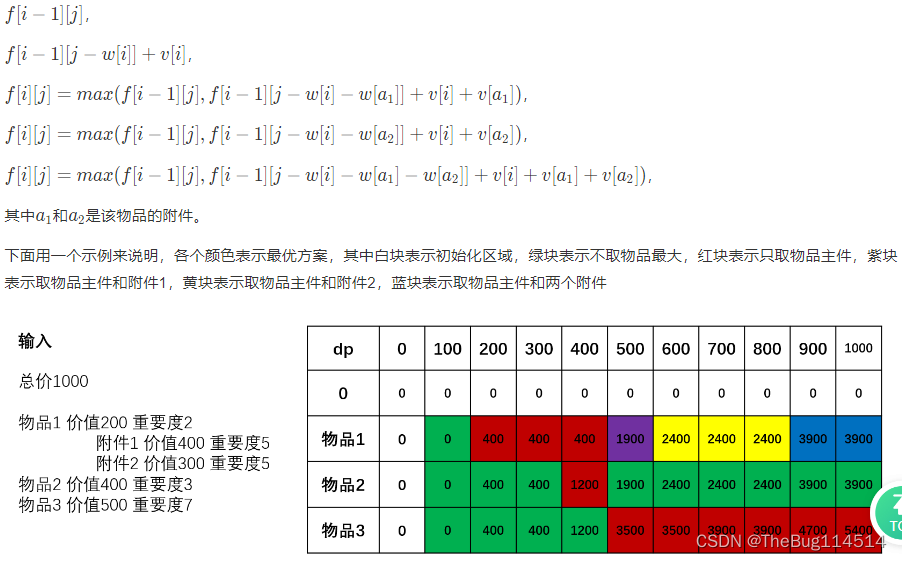
1：购物单（背包问题稍作延申）

输入描述：
输入的第 1 行，为两个正整数N，m，用一个空格隔开：

（其中 N （ N<32000 ）表示总钱数， m （m <60 ）为可购买的物品的个数。）

从第 2 行到第 m+1 行，第 j 行给出了编号为 j-1 的物品的基本数据，每行有 3 个非负整数 v p q

（其中 v 表示该物品的价格（ v<10000 ）， p 表示该物品的重要度（ 1 ~ 5 ）， q 表示该物品是主件还是附件。如果 q=0 ，表示该物品为主件，如果 q>0 ，表示该物品为附件， q 是所属主件的编号）

输出描述：
输出一个正整数，为张强可以获得的最大的满意度。
示例1
输入：

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

输出：

2200

示例2
输入：

50 5
20 3 5
20 3 5
10 3 0
10 2 0
10 1 0

输出：

130

说明：
由第1行可知总钱数N为50以及希望购买的物品个数m为5；
第2和第3行的q为5，说明它们都是编号为5的物品的附件；
第4-6行的q都为0，说明它们都是主件，它们的编号依次为3~5；
所以物品的价格与重要度乘积的总和的最大值为10 * 1+20 * 3+20 * 3=130

---

题解：

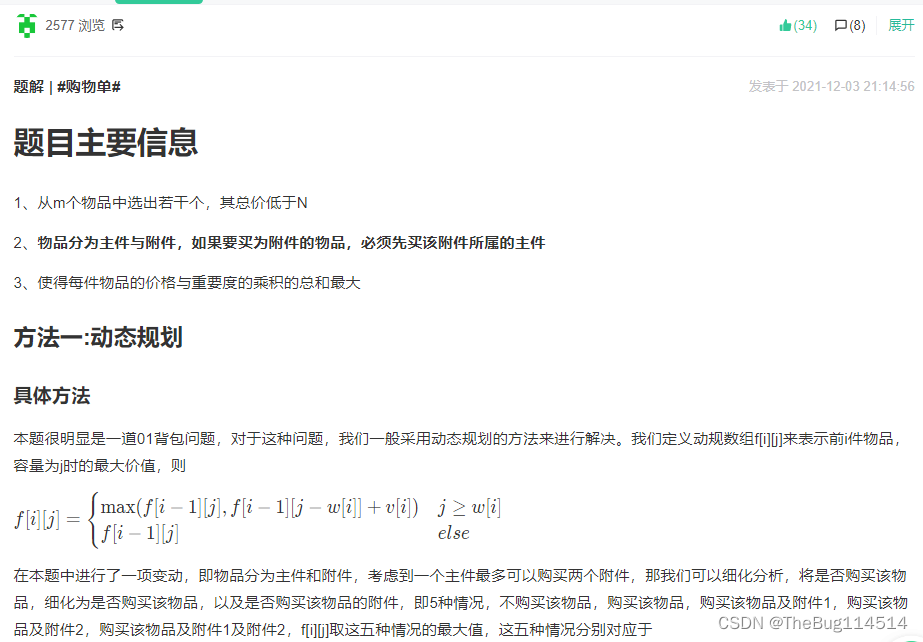
import java.util.Scanner;
 
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        int money = in.nextInt();
        int num = in.nextInt();
        int dp[][] = new int[num+1][money+1];    //dp[i][j]表示前i个物品在容量为j时的最大价值
        Goods[] goods = new Goods[num];
        for(int i = 0; i < num; i++){
            goods[i] = new Goods();
        }
        for(int i=0;i<num;i++){
            int price = in.nextInt();
            int weight = in.nextInt();
            int follow = in.nextInt();
            goods[i].price = price;
            goods[i].weight = weight * price;//直接乘上去方便后面计算
            if(follow == 0){
                goods[i].main=true;
            }else if(goods[follow-1].follow1==-1){
                goods[follow-1].follow1 = i;
            }else{
                goods[follow-1].follow2 = i;
            }
        }
        //初始化完成
        
        for(int i=1;i<=num;i++){
            for(int j=0;j<=money;j++){
                dp[i][j]=dp[i-1][j];    //前i件物品的最大价值至少等于前i-1件物品的最大价值
                //跳过附件，因为附件不能单独直接加入，在加入主件时再考虑附件
                if(goods[i-1].main == false){
                    continue;
                }
                //容量至少要大于物品的价值才考虑要不要买它
                if(j >= goods[i-1].price){
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-goods[i-1].price] + goods[i-1].weight);
                    //如果买了第i个物品能够提高总价值，则买它，否则不动。
                }
                //能买下第i个物品，且也能买下它的第1个附件时
                if(goods[i-1].follow1 != -1 && j >= goods[i-1].price + goods[goods[i-1].follow1].price){
                    dp[i][j]=Math.max(dp[i][j], dp[i-1][j - goods[i-1].price - goods[goods[i-1].follow1].price] + goods[i-1].weight + goods[goods[i-1].follow1].weight);
                }
                //同理，考虑只买第i个物品和它的第2个附件时
                if(goods[i-1].follow2 != -1 && j >= goods[i-1].price + goods[goods[i-1].follow2].price){
                    dp[i][j]=Math.max(dp[i][j], dp[i-1][j - goods[i-1].price - goods[goods[i-1].follow2].price] + goods[i-1].weight + goods[goods[i-1].follow2].weight);
                }
                //最后考虑物品连带2个附件都买的情况
                if(goods[i-1].follow1 != -1 && goods[i-1].follow2 != -1 && j >= goods[i-1].price + goods[goods[i-1].follow1].price + goods[goods[i-1].follow2].price){
                    dp[i][j]=Math.max(dp[i][j], dp[i-1][j - goods[i-1].price - goods[goods[i-1].follow1].price - goods[goods[i-1].follow2].price] + goods[i-1].weight + goods[goods[i-1].follow1].weight + goods[goods[i-1].follow2].weight);
                }
                    
            }
        }
        
        System.out.print(dp[num][money]);
            
            
        
    }
}

class Goods {
    int price;
    int weight;
    boolean main = false;
 
    int follow1 = -1;  //定义附件1的编号
    int follow2 = -1;  //定义附件2的编号
}

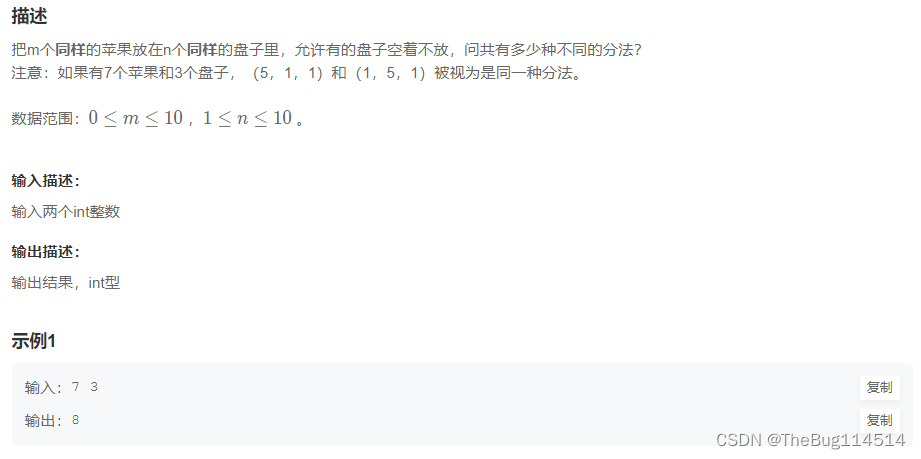
2、放苹果

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int m = in.nextInt();
            int n = in.nextInt();
            int dp[][] = new int[m+1][n+1];	//dp[i][j]表示i个苹果放到j个盘子上的分配情况数量
            if(m == 0 || m == 1 || n == 1){
                System.out.print(1);
                return;
            }
            //0个苹果、1个苹果、1个碟子的情况下都只有一种分配情况
            for(int i=0;i<=n;i++){
                dp[0][i] = 1;
            }
            for(int i=0;i<=m;i++){
                dp[i][1] = 1;
            }
            for(int i=0;i<=n;i++){
                dp[1][i] = 1;
            }
            
            for(int i=2;i<=m;i++){
                for(int j=2;j<=n;j++){
                    if( i < j){
                        dp[i][j] = dp[i][i];
                        //苹果数量小于盘子时，等同于（苹果数量==盘子数量）时的分配方式
                    }else{
                        dp[i][j] = dp[i][j-1] + dp[i-j][j];    
                        //若第j个盘子不装苹果，则分配情况数量等于j-1个盘子的分配情况数量
                        //若第j个盘子装苹果，相当于所有盘子都少装一个苹果，再考虑多出来的苹果的分配；
                    }
                }
            }
            System.out.print(dp[m][n]);
        }
    }
}

3、剪绳子

---

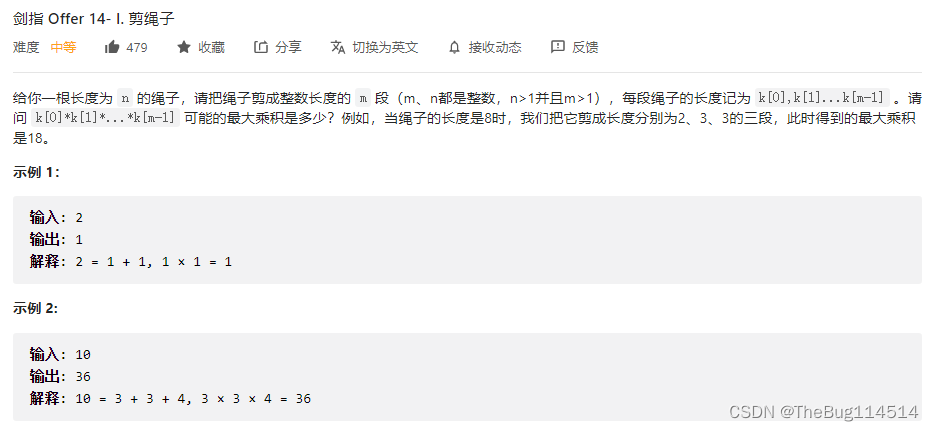
定义dp[i]为前i长度的切割后的最大乘积，i>=2.因为要求切割刀数大于1，所以dp[2] = 1，i从3开始算。

定义变量j表示第一次剪的长度，如果只剪掉长度为1，对最后的乘积无任何增益，所以从长度为2开始剪。

剪了第一段后，剩下(i - j)长度可以剪也可以不剪。如果不剪的话长度乘积即为j * (i - j)；如果剪的话长度乘积即为j * dp[i - j]。取两者最大值max(j * (i - j), j * dp[i - j])

第一段长度j可以取的区间为[2,i)，对所有j不同的情况取最大值，因此最终dp[i]的转移方程为
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))

public int cuttingRope(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for(int i = 3; i < n + 1; i++){
            for(int j = 2; j < i; j++){
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
}

当然通过数学证明可以得知，每段长度为自然对数e时结果最大，因此尽可能选择切割为长度为3的小段效果最好。

---

4、不同的子序列

---

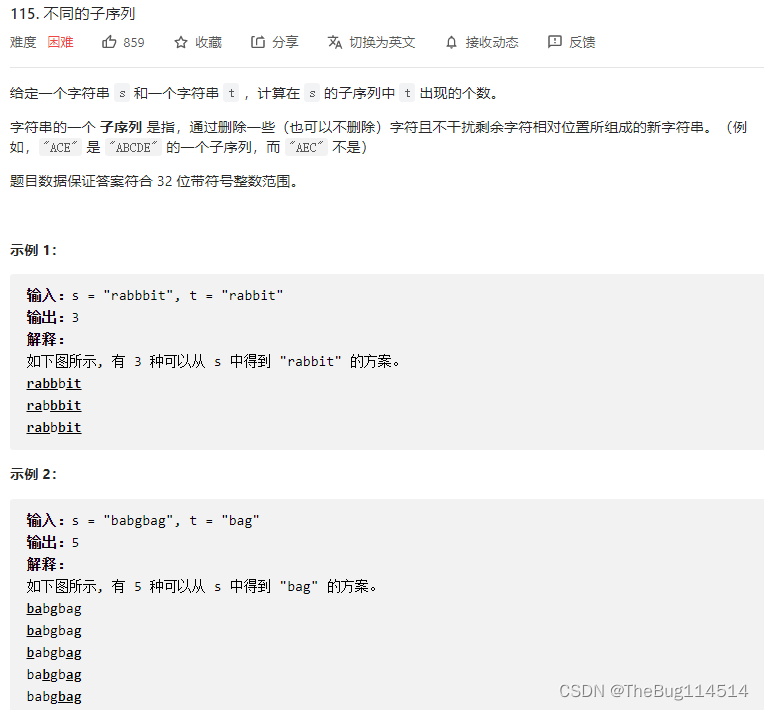
public int numDistinct(String s, String t) {
        if(s.length() < t.length()){
            return 0;
        }
        int m = s.length();
        int n = t.length();
        int[][] dp = new int[m + 1][n + 1]; //s中的i到末尾的子串对应t中j到末尾子串的数量

        //t为空串时，dp[i][n]固定为1
        for (int i = 0; i <= m; i++) {
            dp[i][n] = 1;
        }

        for (int i = m - 1; i >= 0; i--) {
            char sChar = s.charAt(i);
            for (int j = n - 1; j >= 0; j--) {
                char tChar = t.charAt(j);
                //双重循环比较两字符串各个字符
                if (sChar == tChar) {
                    //相等的话，比如aab和ab,那么dp[i][j]可以
                    dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j]; 
                } else {
                    dp[i][j] = dp[i + 1][j];
                }
            }
        }
        return dp[0][0];

    }

总结