一、程序流程图
1. 程序流程图的定义
程序流程图是通过图形符号展示程序控制流程的一种工具。它用一系列的符号来表示程序中的步骤,并通过连接线指示步骤之间的顺序或关系。流程图在编写程序前非常有用,因为它能够帮助开发者理清逻辑,简化复杂的程序结构。
2. 程序流程图的基本符号
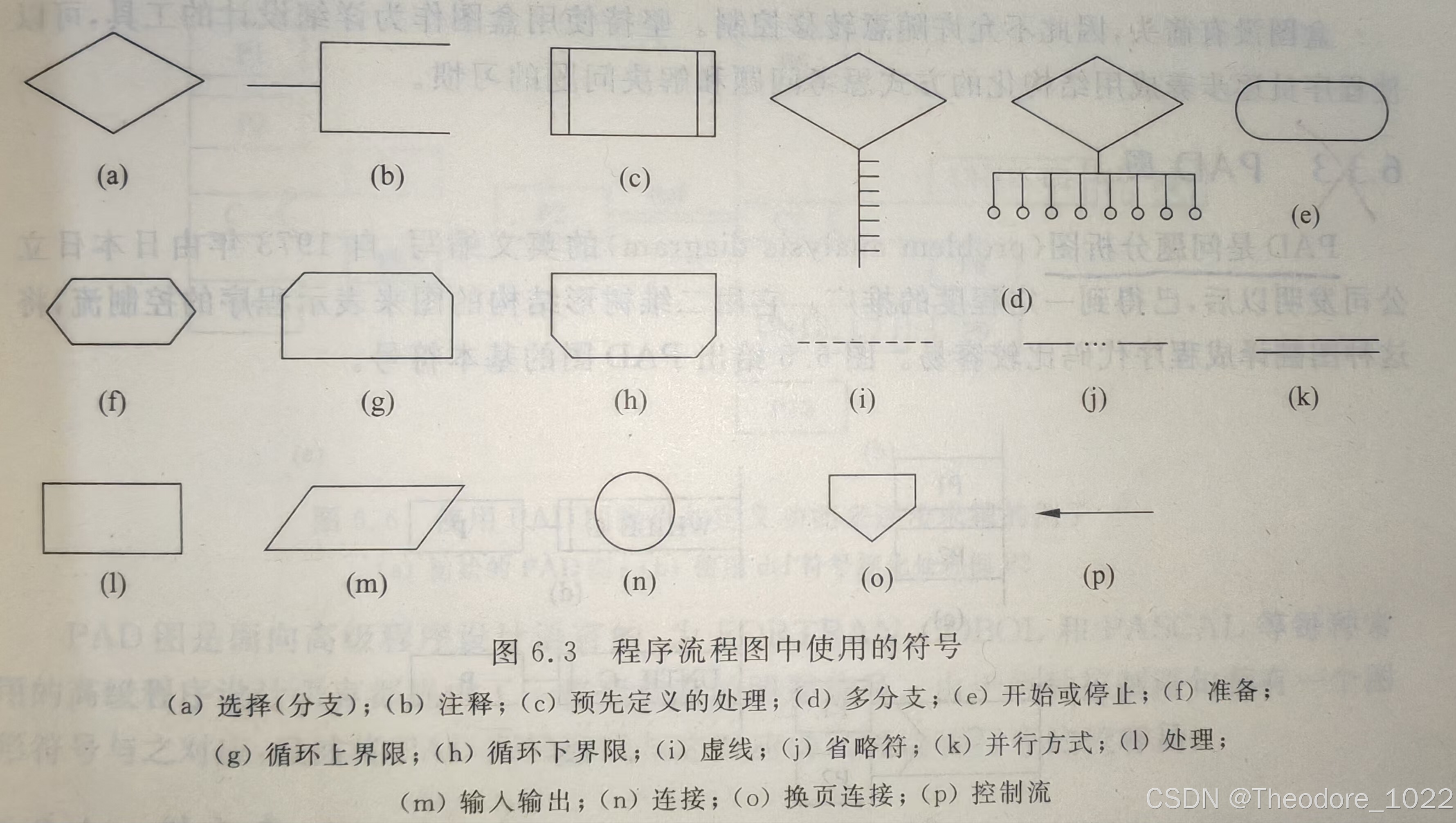
-
起始/结束(Terminator):
- 形状:椭圆形
- 用途:表示程序的开始和结束。
- 示例:程序的开始和结束点。
-
处理步骤(Process):
- 形状:矩形
- 用途:表示一个处理步骤或操作(如计算、赋值)。
- 示例:计算
a = b + c或设置一个变量的值。
-
输入/输出(Input/Output):
- 形状:平行四边形
- 用途:表示输入或输出操作(如读取输入、显示结果)。
- 示例:读取用户输入、打印输出。
-
决策(Decision):
- 形状:菱形
- 用途:表示条件判断或决策操作,通常用于分支结构(如
if、while等)。 - 示例:检查
x > 10或isEven()判断。
-
连接线(Flowline):
- 形状:箭头
- 用途:表示流程图各个符号之间的执行顺序或流程路径。
-
预定义过程(Predefined Process):
- 形状:双矩形
- 用途:表示一个已经定义的过程或子程序。
- 示例:调用一个子函数或模块。
-
注释(Annotation):
- 形状:带有弯曲边的矩形
- 用途:用于在流程图中添加说明或注解,提供更多的上下文信息。
3. 程序流程图的基本结构
- 开始:流程图从“起始”符号开始,表示程序的启动。
- 输入:根据需要,流程图中可能会有“输入”步骤,表示获取外部数据(例如,从用户获取输入)。
- 处理:处理符号用于表示计算、赋值等操作。
- 决策:决策符号通常用于表示判断条件,决定接下来程序执行的路径。通常有“是”或“否”两个分支。
- 输出:输出符号表示程序结果或数据的输出。
- 结束:流程图通过“结束”符号表示程序的终止。
4. 程序流程图的应用
- 帮助理解程序逻辑:开发人员可以通过流程图清晰地理解程序的各个步骤和执行顺序,减少错误。
- 调试与测试:通过流程图可以更清晰地看出程序的流程,有助于定位逻辑错误或调试问题。
- 与团队沟通:流程图为团队成员之间的沟通提供了可视化的手段,有助于讨论和修改程序逻辑。
- 编写文档:流程图也可以作为程序文档的一部分,帮助后续的开发者快速理解程序的工作原理。
5. 程序流程图的优点
- 可视化:通过图形化的方式展示程序流程,易于理解和分析。
- 简洁明了:流程图使得复杂的程序逻辑简化为直观的图形,方便开发和讨论。
- 易于调试:通过分析流程图,开发人员可以发现逻辑错误或不合理的地方。
- 便于修改:在需求变化时,修改流程图比修改代码本身更简单。
6. 程序流程图的缺点
- 规模限制:对于大型系统或复杂程序,流程图可能变得过于复杂,难以维护。
- 细节不足:流程图通常只关注程序的控制流,对于细节(如函数内部的实现、数据结构等)表现不充分。
- 不适合动态行为:程序流程图主要适用于静态逻辑的表示,对于动态的实时行为表现不佳。
二、盒图
1. 盒图的定义
结构化控制结构的盒图是一种图形化表示程序控制结构的工具,它通过不同的图形元素来表示程序中的控制流。控制流可以是顺序执行、条件分支或循环结构。通过这种图形化的表示,设计者可以清晰地描述程序中各个功能模块如何按照特定的顺序、条件或循环逻辑执行。
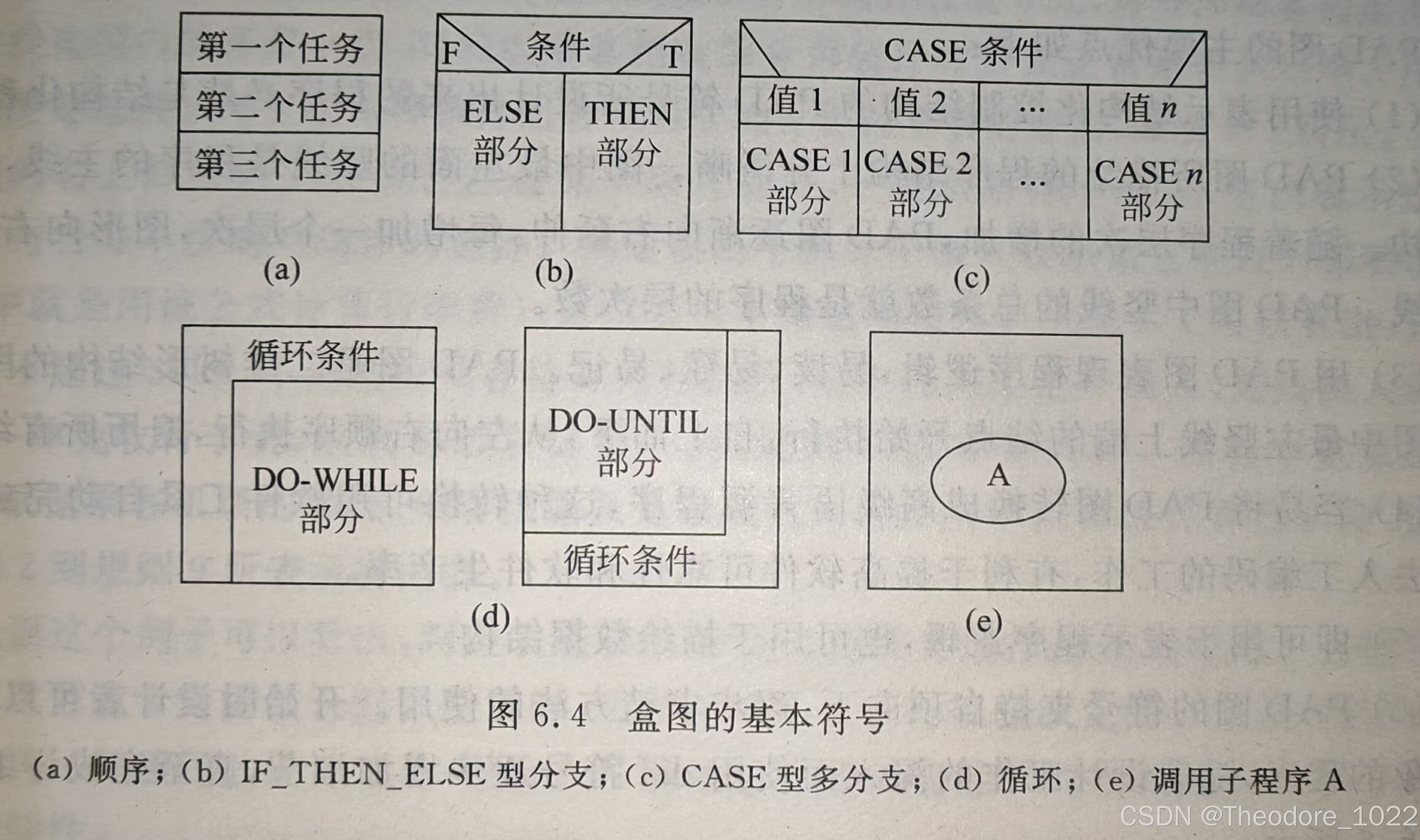
2. 结构化控制结构的三种基本类型
(1)顺序结构(Sequence Structure)
顺序结构表示程序中按顺序依次执行的语句,控制流从上到下依次执行,没有任何分支或跳转。
特点:
- 语句按顺序执行。
- 没有条件判断或循环。
盒图表示:
- 顺序结构通常表现为一个简单的矩形框,框内包含要执行的程序步骤或操作。
(2)选择结构(Selection Structure)
选择结构表示在程序中基于某些条件来决定执行路径,即根据条件判断来选择不同的执行分支。选择结构常见的形式有 if-else 语句或 switch-case 语句。
特点:
- 具有条件判断。
- 根据判断的结果选择执行不同的语句块。
盒图表示:
- 选择结构用一个条件判断框表示,框内标明条件表达式。
- 通过箭头表示不同条件下的执行路径。
(3)循环结构(Loop Structure)
循环结构表示程序根据某种条件重复执行某一段代码,直到满足退出条件。常见的循环结构包括 while 循环、for 循环等。
特点:
- 有一个循环条件,满足条件时会重复执行。
- 循环体执行完后,控制流会返回判断条件,继续判断是否需要再次执行循环体。
盒图表示:
- 循环结构用一个框来表示循环体,并通过箭头表示执行的回溯到条件判断的路径。
- 循环框通常会连接一个判断条件,判断条件决定是否继续执行循环体。
3. 结构化控制结构的应用
结构化控制结构图广泛应用于程序设计和分析过程中,尤其在以下场景中:
- 程序设计:设计程序时,使用盒图帮助明确控制流,确保程序逻辑清晰、易于实现和维护。
- 程序优化:通过结构化控制流的设计,可以减少代码中的冗余逻辑,使程序更简洁、可读。
- 模块化设计:盒图可以清晰地展示每个模块或功能块的执行流程,帮助开发人员理解和分解问题。
三、判定表
1. 判定表的定义
判定表是一种用于表示决策逻辑的工具,它以表格的形式列出所有条件的组合及其对应的动作或决策结果。每一列代表一个条件的状态,每一行表示一个条件组合的决策结果。判定表帮助决策者明确不同条件下的动作,并通过视觉化方式清晰地展示各种组合条件的影响。
2. 判定表的基本组成
- 条件部分:列出影响决策的条件,每个条件可能有多个状态或值。例如:是否已付款、是否库存充足等。
- 动作部分:规定针对条件组合应采取的行动或决策结果。例如:发货、退款、提示用户等。
- 规则部分:判定表的行部分,表示不同的条件组合以及每个条件组合下的动作或结果。每一行代表一个规则。
3. 判定表的基本结构
一个典型的判定表通常包含四个区域:
- 条件(Conditions):列出需要判断的各个条件。
- 规则(Rules):列出每个规则的具体情况。
- 动作(Actions):根据条件组合执行的动作或决策。
- 决策(Decision):最终决定根据条件组合采取的动作或结果。
4.判定表的样式

5. 判定表的示例
假设我们有一个简单的订单处理系统,根据客户的付款状态、库存情况以及订单金额来决定是否发货、是否退款等。以下是一个简单的判定表:
订单处理判定表:
| 规则 | 条件1(是否付款) | 条件2(库存充足) | 条件3(订单金额) | 动作1(发货) | 动作2(退款) | 动作3(发货通知) |
|---|---|---|---|---|---|---|
| 规则1 | 是 | 是 | 大于100元 | 是 | 否 | 是 |
| 规则2 | 是 | 否 | 大于100元 | 否 | 是 | 否 |
| 规则3 | 否 | 是 | 大于100元 | 否 | 是 | 否 |
| 规则4 | 是 | 是 | 小于100元 | 是 | 否 | 是 |
| 规则5 | 否 | 否 | 小于100元 | 否 | 是 | 否 |
解释:
- 规则1:如果已付款且库存充足且订单金额大于100元,则发货,并通知用户发货。
- 规则2:如果已付款但库存不足且订单金额大于100元,则退款。
- 规则3:如果未付款但库存充足且订单金额大于100元,则退款。
- 规则4:如果已付款且库存充足且订单金额小于100元,则发货,并通知用户发货。
- 规则5:如果未付款且库存不足且订单金额小于100元,则退款。
6. 判定表的优点
- 清晰明确:通过表格的形式,将所有条件和动作一目了然地列出,避免遗漏复杂的条件组合。
- 避免遗漏条件:判定表通过列出所有可能的条件组合,确保不漏掉任何可能的情况。
- 逻辑简化:通过将复杂的决策逻辑转换为表格形式,可以帮助开发人员更好地理解系统的行为,并提高维护性。
- 自动化生成:判定表可以帮助生成测试用例,确保不同条件下的系统行为被充分测试。
7. 判定表的缺点
- 复杂性:当条件数目较多时,判定表的规模会变得庞大,可能会导致表格过于复杂,难以维护。
- 冗余:在一些情况下,不同的规则可能会有重复的动作或条件,判定表可能出现冗余。
- 难以表示复杂的动作:如果动作比较复杂,判定表可能不适合进行详细描述。
四、判定树
1. 判定树的定义
判定树是一种树形结构,每个内部节点表示一个决策条件,节点的每条边表示不同的条件结果,叶子节点则表示最终的决策或动作。判定树通过递归地将问题拆解成更小的子问题,帮助决策者逐步进行选择,直到到达最终决策。
2. 判定树的组成
-
根节点(Root Node):判定树的起始点,表示最初的决策问题。根节点通常是一个条件或问题。
-
内部节点(Internal Nodes):每个内部节点代表一个判断条件,节点分支表示不同的条件取值。每个分支代表对该条件判断结果的不同响应。
-
叶子节点(Leaf Nodes):叶子节点表示决策树的最终结果,通常是一个具体的决策、建议或行动。每个叶子节点都表示在当前条件组合下的最终结果。
-
边(Edges):边表示从一个节点到另一个节点的决策路径,通常根据条件判断的不同取值有不同的分支。
3. 判定树的结构
- 从根节点出发,按不同条件的取值沿不同路径走,直到最终到达一个叶子节点,表示最终决策。
- 每个路径代表从根节点到叶子节点的一系列决策过程,最终的叶子节点即为结果。
4. 判定树的示例
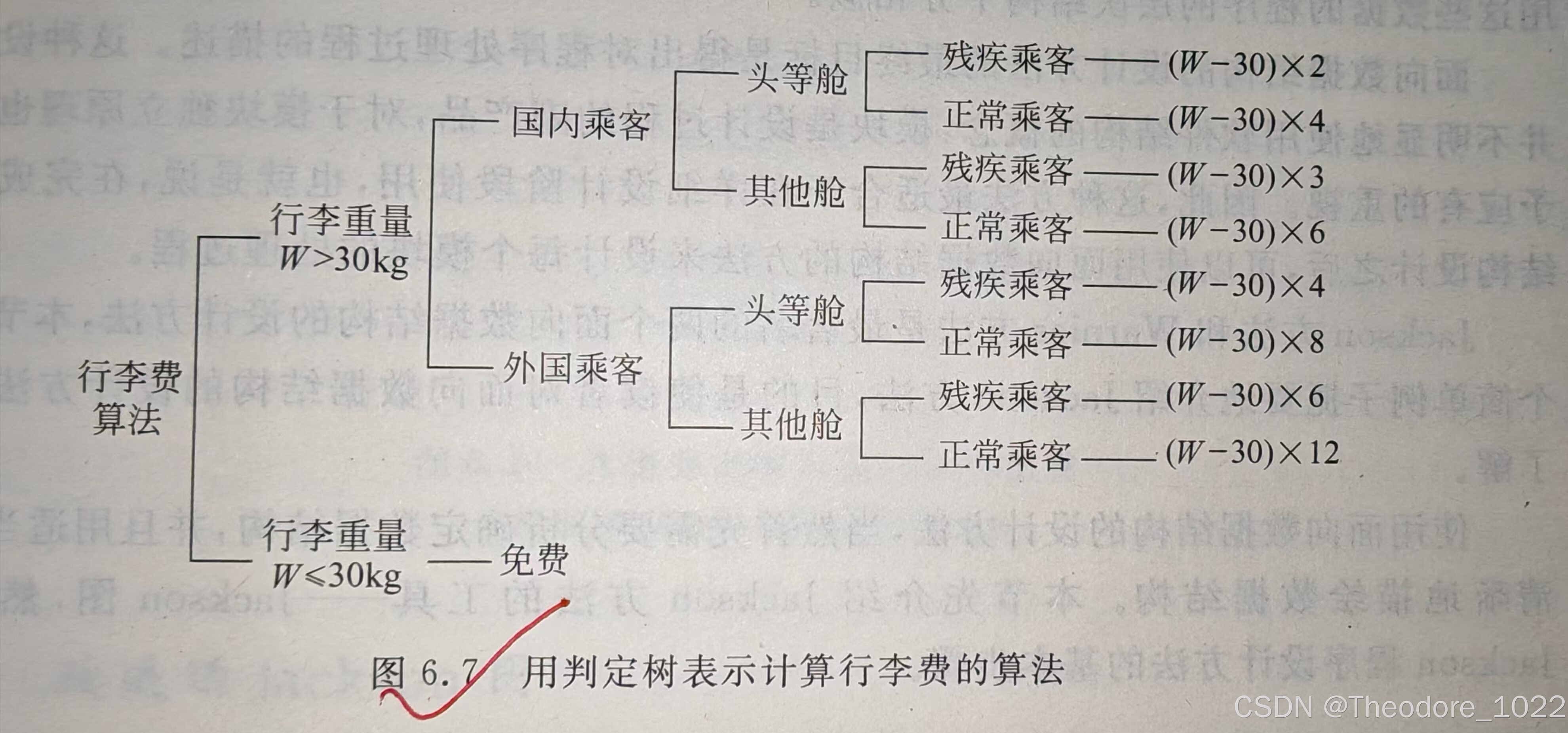
5. 判定树的优点
- 直观性:判定树的结构是树形的,容易理解和直观地表示决策过程,帮助决策者清楚地看到每个步骤。
- 简化复杂决策:将复杂的决策过程通过分层次的判断条件逐步细化,使决策过程更加明确。
- 适应性强:判定树适用于多种决策问题,尤其是条件多、规则复杂的情况。
- 可视化支持:判定树图形化的表示方式非常适合展示和分析,尤其在决策分析、机器学习等领域中应用广泛。
6. 判定树的缺点
- 树的膨胀:当条件过多时,判定树的结构会变得非常复杂,导致树的膨胀。每增加一个条件,树的分支数量都会急剧增加。
- 过拟合问题:在某些情况下,如果判定树太复杂,容易出现过拟合现象。即模型过于关注训练数据中的细节,而忽略了数据的通用规律,导致模型在新数据上的表现较差。
- 维护困难:如果规则和条件经常发生变化,维护复杂的判定树可能会变得困难。
7. 判定树的应用
- 专家系统:在专家系统中,判定树用于推理和决策,模拟专家根据一系列条件做出判断的过程。
- 机器学习:在机器学习中,判定树是分类和回归问题中的一种基础算法(如 决策树算法)。
- 业务决策:在金融、医疗、保险等行业,判定树被用来帮助决策者根据多个条件做出决策。
- 流程控制:在自动化系统中,判定树被用来控制不同的工作流程,自动判断应该执行哪一部分操作。
五、Jackson图
1. Jackson图的定义
Jackson图是一种图形表示法,用来描述数据从输入到输出的转换过程,它通过图形化的方式表示数据的流动、处理和转换。它的主要目的是通过明确显示数据流和相关过程,帮助开发人员理清系统设计中的数据处理和控制逻辑。
2. Jackson图的基本组成
-
数据流(Data Flow):数据流是Jackson图中的核心元素,表示数据从一个模块流向另一个模块的过程。通常用箭头表示,箭头指示数据流动的方向。
-
处理节点(Process Nodes):处理节点表示对数据进行处理的操作。在Jackson图中,处理节点用矩形框表示。每个处理节点都包含某种数据操作或变换,例如计算、验证或转换等。
-
输入输出端(Input/Output):输入端表示系统接收的数据源,输出端表示系统产生的数据结果。通常在图的边缘标记输入和输出。
-
条件分支(Decision Nodes):如果系统中有条件判断或分支决策,通常会使用条件节点表示。在Jackson图中,条件节点用菱形表示,并且会根据条件的不同生成不同的数据流路径。
-
数据存储(Data Stores):数据存储用来表示数据的长期保存和中间存储。它们通常以双线矩形框表示,表示数据在系统中被存储。
-
连接(Connectors):连接用于连接不同的模块和节点,表示数据流动的路径。它们通常通过箭头或者线条连接各个处理节点、输入输出端和数据存储。
3. Jackson图的结构
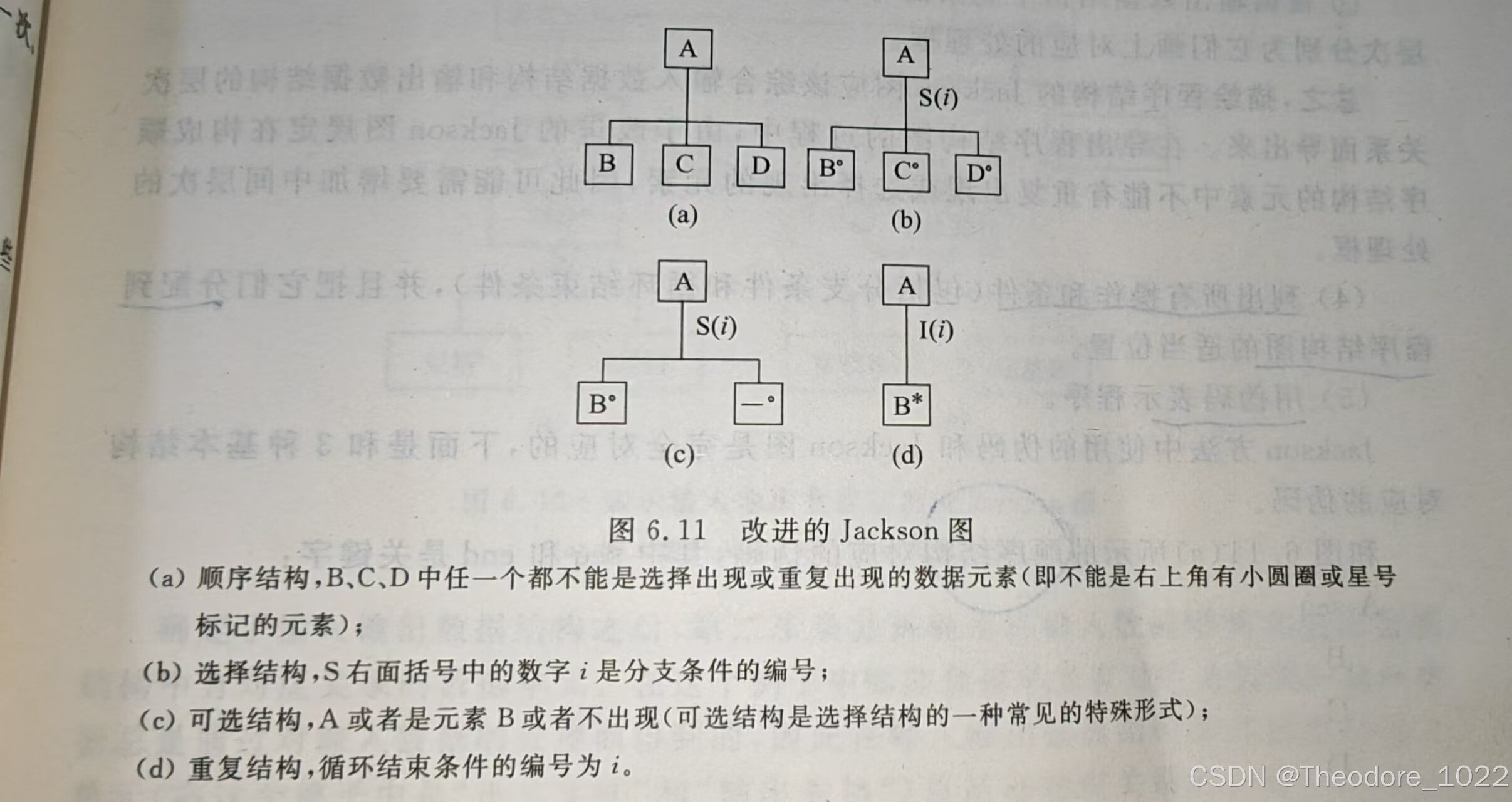
Jackson图的结构一般呈现层次化的组织方式,通常遵循自顶向下的设计方法,逐渐细化系统的处理流程和数据流动。图的顶端表示最初的输入和初始的处理过程,随着设计的深入,逐步展开各个细节部分,直到最终的输出。
4. Jackson图的表示方法
在Jackson图中,系统的设计可以被逐步分解成若干个小模块,每个模块代表一个数据处理过程。每个模块通过数据流连接,表现出数据在各个处理环节之间的流动。以下是Jackson图的一般表示方法:
-
图形化表示:
- 用箭头表示数据流动。
- 用矩形表示处理过程。
- 用双线矩形表示数据存储。
- 用菱形表示条件判断。
-
层次化表示:
- Jackson图支持层次化建模,可以从高层次开始,逐步细化,逐级分解系统的处理过程,直至每个具体操作步骤。

5. Jackson图的优点
- 清晰的表示数据流:Jackson图能够清晰地描述系统中数据流动的路径和过程,使得开发人员可以更容易理解数据如何从输入到输出进行处理。
- 直观性:图形化表示方式让人一目了然,便于与其他开发人员、设计人员和非技术人员进行沟通。
- 良好的层次性:Jackson图采用层次化的结构,能够帮助开发人员在不同的抽象层次上思考和设计系统。
- 便于分析系统中的数据依赖:通过Jackson图,可以清晰地看到系统中的数据依赖关系,有助于发现潜在的性能瓶颈或数据处理中的逻辑问题。
6. Jackson图的缺点
- 复杂性:对于复杂的系统,Jackson图可能变得非常庞大,尤其是在多层次、多模块的系统中,图形的复杂度会使得维护变得困难。
- 过于静态:Jackson图主要关注数据流和静态处理流程,对于系统中的动态变化(如事件驱动、并发控制等)描述得较少。
- 难以表示细节:如果需要表达复杂的业务逻辑或详细的处理步骤,Jackson图可能无法清晰、全面地表示,尤其是在没有分层处理的情况下。
7. Jackson图的应用
- 系统设计:在系统设计阶段,使用Jackson图能够帮助开发人员理清数据流动和处理逻辑,尤其是在进行数据转换或数据仓库设计时尤为有用。
- 数据流程建模:在处理数据的流动、存储和转换时,Jackson图提供了一个清晰的视角,帮助设计者理解数据在不同模块之间的流动。
- 业务流程建模:在业务流程建模中,Jackson图可以帮助组织和企业清晰地表达复杂的工作流和决策过程,确保数据能够在各个环节中流转。
六、程序复杂度
1.McCabe方法的定义
McCabe方法通过圈复杂度来衡量程序的复杂度。它的基本思想是:
- 程序的每个决策点(如
if、for、while等循环语句)都增加了一个分支,使得代码的控制流变得更加复杂。 - 圈复杂度是通过计算控制流图中独立路径的数量来得出的,每条独立路径都代表了一条代码路径,可以通过不同的条件组合来执行。
- 圈复杂度的目的是衡量程序中独立路径的数量,从而评估程序的复杂度和可测试性。
2.环形复杂度的方法
① 边数 - 点数 + 2
② 判定节点数 + 1
③ 线性无关的区域数
3. McCabe方法的优点
- 简单直观:圈复杂度的计算方法相对简单,易于理解和应用。
- 度量可测试性和维护性:它可以直观地反映出代码的复杂度,从而有助于评估代码的可测试性和可维护性。
- 帮助代码重构:通过发现高复杂度的部分,McCabe方法能帮助开发者识别需要重构的代码块,从而提升代码的质量。
- 广泛使用:圈复杂度已经成为衡量代码复杂度的一个标准工具,很多代码质量分析工具都能计算圈复杂度。
4. McCabe方法的缺点
- 仅关注控制流:圈复杂度主要考虑控制流,而不考虑数据流、模块间的依赖等其他因素,因此无法全面评价代码的复杂性。
- 不考虑外部因素:它不能反映外部条件或环境的复杂性。例如,调用外部库或数据库等的操作不会影响圈复杂度,但这些操作可能会增加系统的复杂性。
- 过高的复杂度未必不良:有些情况下,某些复杂的控制流结构是不可避免的或是为实现某些高级功能所必需的,因此圈复杂度过高不一定意味着代码质量差。

























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








