摘自于编程珠玑第二章,加入了一些自己的东西。
看起来很困难的问题也可以有一个简单的、意想不到的答案。拿到一个问题,不要急于完成程序的实现,静下心来多想一想。
首先我们来看两个问题的描述:
一、将一个n元的一维向量顺时针或逆时针旋转i个位置,要求其时间复杂度为O(n),空间复杂度为O(1),比如n=8,i=3时,向量abcdefg顺时针旋转为defghabc。
二、给定一个英语字典,找出其中所有的变位词集合。比如,“ports”、“stop”和“tops”互为变位词,因为每个单词都可以通过改变其他单词中字母顺序来得到。
下面分别就这两个问题给予讨论,你可能会发出感叹我咋没有想起来呢,怎么这么巧呢。
问题一:我们可以将该问题转换为数组ab转换为ba,同时假定我们拥有函数reverse可以将数组中特定部分的元素求逆。首先介绍一下本科时期学过的数学矩阵公式:
可改写为
通过上面公式,对于ab我们可以先对a求逆,然后对b求逆,得到。最后在整体求逆,从而恰好得到ba,
即:reverse(0,i-1);reverse(i,n-1);reverse(0,n-1);其时间复杂度为,空间复杂度为。
引申:如何将向量abc变为向量cba??
当然你可以这样做:假设该向量为array,length(a),length(b),length(c),然后比较length(a)与length(c)的大小,假设length(a)>length(c).
for(inti=0;i<length(c);i++)
{
swap(array[i],array[length(a)+length(b)+i]);
}
下面即是对数组array【i=length(c)……length(abc)】进行逆时针循环移位length(a)-length(c)
移位操作转换为array【i=length(c)……length(a)-1】array【i=length(a)……length(abc)】的置换,似乎看起来程序代码看起来较为复杂,但其时间复杂度为,空间复杂度为。
现利用矩阵求逆的性质对其简单化:
具体算法同上述。
问题二:对字典中的每一个单词进行标识,使得在相同变位词类中的单词具有相同的标识,然后将所有相同标识的单词集中在一起。这样就将原始的变位词问题简化两个子问题:选择标识和集中具有相同标识的单词。
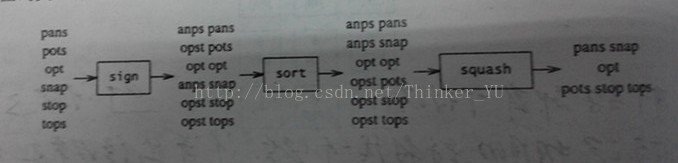
该程序按照三个阶段:第一个程序标识单词(将单词中的字母按照字母表顺序排列);第二个程序排序标识后的文件,而第三个程序将这些单词压缩为每个变位词类一行的形式。
具体算法可参看编程珠玑(第二版),第18页。






















 1472
1472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








