【每日一题Day25】LC790多米诺和托米诺平铺

本文链接：https://blog.csdn.net/Tikitian/article/details/127820285

多米诺和托米诺平铺【LC790】

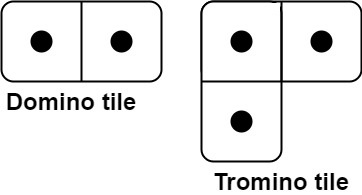
You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

又是没做过的题型

思路：使用状态机DP，定义第i列瓷砖的四种不同状态【未铺满】，第i列瓷砖的状态可由前一列的瓷砖状态得到，最终dp[i][1]即为前i列瓷砖被铺满的方案数
- j=0时，代表第i列未被填充
- j=1时，代表第i列两个方块均被填充
- j=2时，代表第i列上面的方块被填充
- j=3时，代表第i列下面的方块被填充

动态规划实现

确定dp数组（dp table）以及下标的含义

dp[i][j]:当前i-1列铺满时，当前第i列状态为j时的方案数

j的取值范围为[0,4)
- j=0时，代表第i列未被填充
- j=1时，代表第i列两个方块均被填充
- j=2时，代表第i列上面的方块被填充
- j=3时，代表第i列下面的方块被填充
确定递推公式
- dp[i][0]：前i-1列被填充满，第i列未被填充
  - 只能由dp[i-1][1]转移：在第i-1列竖放2*1的骨牌
  dp[i][0] = dp[i-1][0]
- dp[i][1]：前i列均被填充
  - 由dp[i-1][0]转移：在第i-1列和第i列横放1*2的骨牌
  - 由dp[i-1][1]转移：在第i-1列和第i列竖放2*1的骨牌
  - 由dp[i-1][2]转移：横放一块L型骨牌
  - 由dp[i-1][3]转移：横放一块L型骨牌
  dp[i][1] =dp[i-1][0]+ dp[i-1][1] + dp[i-1][2] + dp[i-1][3]
- dp[i][2]：前i-1列被填充满、第i列上面的方块被填充
  - 由dp[i-1][0]转移：横放一块L型骨牌
  - 由dp[i-1][3]转移：横放一块L型骨牌
  dp[i][2] = dp[i-1][0] + dp[i-1][3]
- dp[i][3]：前i-1列被填充满、第i列下面的方块被填充
  - 由dp[i-1][0]转移：横放一块L型骨牌
  - 由dp[i-1][2]转移：横放一块L型骨牌
  dp[i][3] = dp[i-1][0] + dp[i-1][2]
dp数组如何初始化

dp[1][0]=1

dp[1][1]=1

dp[1][2]=0

dp[1][3]=0
确定遍历顺序
- 正序遍历i
举例推导dp数组

dp[i][0] dp[i][1] dp[i][2] dp[i][3]
1 1 1 0 0
2 1 2 1 1
3 2 5 2 2
4 5 11 4 4

	dp[i][0]	dp[i][1]	dp[i][2]	dp[i][3]
1	1	1	0	0
2	1	2	1	1
3	2	5	2	2
4	5	11	4	4

代码

class Solution {

    public int numTilings(int n) {
        int MOD = (int)1e9 + 7;
        int[][] dp = new int[n+1][4];
        dp[1][0] = 1;
        dp[1][1] = 1;
        for (int i = 2; i <= n; i++){
            dp[i][0] = dp[i-1][1] % MOD;
            for (int j = 0; j < 4; j++){
                dp[i][1] = (dp[i][1] + dp[i-1][j]) % MOD;
            }
            dp[i][2] = (dp[i-1][0] + dp[i-1][3]) % MOD;
            dp[i][3] = (dp[i-1][0] + dp[i-1][2]) % MOD;
        }
        return dp[n][1];
    }
}

复杂度
- 时间复杂度： $O (n)$
- 空间复杂度： $O (n)$

滚动数组优化

int a = i & 1

奇数1 偶数0，确定下标
int b = (i - 1) & 1

奇数0 偶数1

class Solution {
    public int numTilings(int n) {
        int MOD = (int)1e9 + 7;
        int[][] dp = new int[2][4];
        dp[1][0] = 1;
        dp[1][1] = 1;
        for (int i = 2; i <= n; i++){
            int a = i & 1;// 奇数1 偶数0
            int b = (i-1) & 1;// 奇数0 偶数1
            dp[a][0] = dp[b][1];
            int cur = 0;
            for (int j = 0; j < 4; j++){
                cur = (cur + dp[b][j]) % MOD;
            }
            dp[a][1] = cur;
            dp[a][2] = (dp[b][0] + dp[b][3]) % MOD;
            dp[a][3] = (dp[b][0] + dp[b][2]) % MOD;
        }
        return dp[n & 1][1];
    }
}