bzoj 1597: [Usaco2008 Mar]土地购买（斜率优化dp 例题）

Description

农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.

Input

• 第1行: 一个数: N

• 第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽

Output

• 第一行: 最小的可行费用.

题解：

本题是一道斜率优化的比较经典的题目，可以作为例题来学一下，我做这道题是为了巩固一下之前刚学的斜率优化，结果WA了好多次，整整卡了三天。。下面讲一下我的一些理解：

-> 不会斜率优化的童鞋可以去看我的另一篇博文，那是一道非常裸的斜率优化dp模板题，里面有讲解 <-

本题并不是非常裸的斜率优化，需要一点小小的预处理。
我们定义w[i]为第i快土地的宽度，l[i]为第i快土地的长度然后可以将所有的土地按照长度排序（按照宽度排序一样，没有太大差别），这是我们可以发现如果对于两块土地i，j（j>i），w[j]>=w[i]，那么就说明第j块土地的长和宽都比第i块土地大，那么在购买第j块土地时，如果附带购买第i块土地的话是不用支付额外的费用的，我们将这样的土地删去，之后我们剩下的土地就是一个长度单调不减，宽度单调递增的序列，然后我们就可以dp了。
先写出本题的dp方程：
f[i]=min( f[j]+w[j+1]*l[i] )；（i>j）
由于之前我们的预处理，那么第j+1到第i块土地间的长度最大值就是第i块，宽度最大值就是第j+1块，所以我们枚举i块之前的每块土地，假设我们上一次决策是买下第j块后结账，那么我们这次决策就要买下第j+1块到第i块，然后取最优值即可；
这样无疑是很慢的，n^2的复杂度，接下来就是斜率优化出场了：
我们还是按照老套路设G=f[i]，y=f[j]，k=l[i]，x=w[j+1];
那么式子就是 G=y+k*x
即 ：y=-k*x+G;
这样每块土地的决策就可以抽象成一个点。
这时我们会发现k是单调递增的，y是单增的，但是x是单减的，而且前面有一个负号，这样的形式显然是不能做斜率优化的。
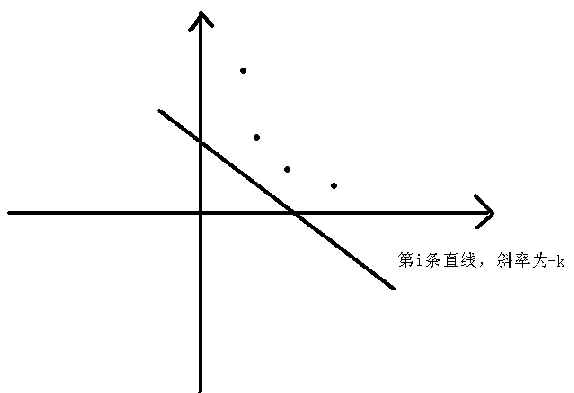
首先让我们来观察一下这个图像：

这时很显然是不符合斜率优化的条件的，或者说很难搞。
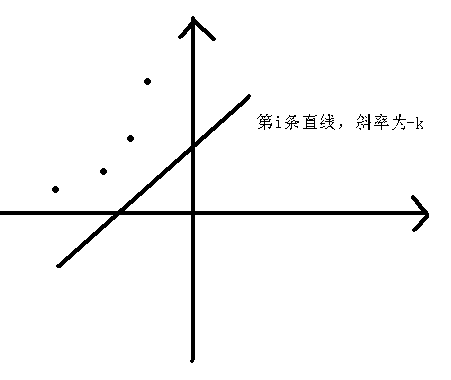
那我们就可以把图像关于y轴对称一下，得到下面的图像：

这就是我们想要的图像啦！（象限不用管它，因为不影响结果）

还记得我们刚才的变量的意义和它们的解析式么？
G=f[i]，y=f[j]，k=l[i]，x=w[j+1];
y=-k*x+G;
这时由于我们的对称操作，斜率和x坐标都变成了相反数，所以我们可以令x=-w[j+1]，k不变,解析式就变成了y=k*x+G；这时x，y，k均是单增的就可以进行优化了！
之后的操作都和斜率优化一样了，建一个队列，存储已经加入点，建立指针指向当先的队首元素，然后枚举判断斜率即可。

我的错是出在宏定义上面！！我一直把宏定义当一个函数用，其实不是的，它的执行过程应该是将源代码中出现宏定义的地方替换掉！所以在宏定义中有符号时注意要加括号，不然在代码中出现时可能会出现符号问题；
还有就是要注意精度，强制类型转换时要把每一步都转换一遍！我一开始时用乘法的，结果炸long long，然后改成double，结果精度出了bug，，又是无限的WA，还好有小号。不然准炸飞 >_<

由于之前讲过斜率优化，所以本篇博文比较简略，有不懂的地方可以去看我的另一篇博文 ->再次推荐qwq <-

代码如下（略丑，尤其是类型转换部分，，因为实在是懒得改了>_<）：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 50010
#define x(i) (s[i+1].w*(-1))
#define y(i) f[i]
using namespace std;
struct ground { long long l,w; }s[N];
long long f[N],dl[N],top,tail,n;
bool cmp(ground x,ground y) { return x.l==y.l?x.w<y.w:x.l<y.l; }
bool check1(long long i,long long j,long long k) {
    return (double)((double)(y(j)-y(i))/(double)(x(j)-x(i)))<=(double)k;
}
bool check2(long long i,long long j,long long now) {
    return (double)((double)(y(now)-y(j))/(double)(x(now)-x(j)))<=(double)((double)(y(j)-y(i))/(double)(x(j)-x(i)));
}
void copy(long long i,long long j) {
    s[i].l=s[j].l;s[i].w=s[j].w; return;
}
long long in() {
    char c=0;long long s=0;
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') s=s*10+c-'0',c=getchar();
    return s;
}
int main() {
    n=in(); for(int i=1;i<=n;i++) s[i].l=in(),s[i].w=in();
    sort(s+1,s+n+1,cmp);int now=1;
    for(int i=1;i<=n;i++) {
      while(now>0&&s[i].w>=s[now].w) now--;
      copy(++now,i);
    } top=tail=1;
    for(int i=1;i<=now;i++) {
      long long k=s[i].l;
      while(top<tail&&check1(dl[top],dl[top+1],k)) top++;
      f[i]=f[dl[top]]+k*s[dl[top]+1].w;
      while(tail>top&&check2(dl[tail-1],dl[tail],i)) tail--;
      dl[++tail]=i;
    } printf("%lld",f[now]);
}