目录
NSSCTF [HNCTF 2022 WEEK2] ——littleLattice
格的定义

举个例子
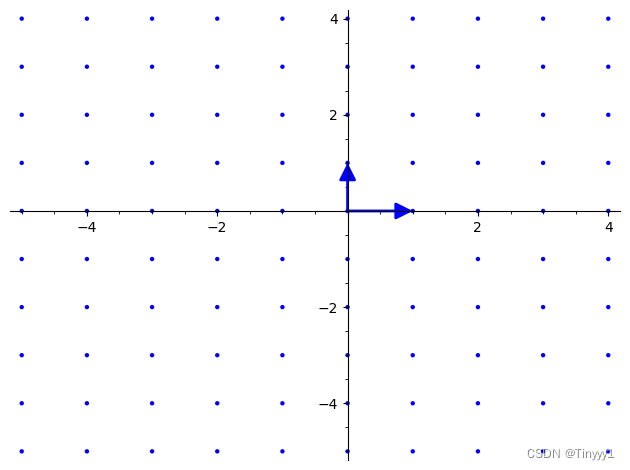
上图为2维空间中的一个格,这个格的基为(0,1),(1,0)
不同的基有可能生成同样的格。
同样是这个二维空间的格,我们可以用下面这个基构成
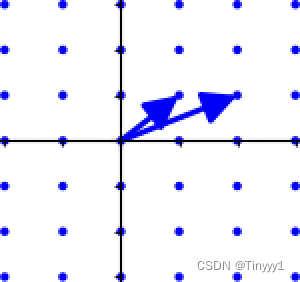
这组基为(1,1),(2,1)
注:基底都是互为线性不相关的,线性元素只能取整数
SVP问题
在格子上找到一个范数最小的向量。范数就可以理解为长度
比如向量(a,b),那么它的范数就是.
从二维来看,这个问题就非常简单。比如一组基底为(1,0),(0,1)构成的格,它的最短向量就是1。
如果维度特别大,这个问题就会非常复杂。
有一个非常神奇的算法:LLL算法。
给定一个n维的格子,它会返回给你n个可能不是最短但是非常短的向量,这些向量之间正交性很好,范数很小。
正交的概念:
垂直
二维:(1,0),(0,1)
三维:(0,0,1),(0,1,0),(1,0,0)
四维:(0,0,0,1),(0,0,1,0),(0,1,0,0),(1,0,0,0)
Hermite定理
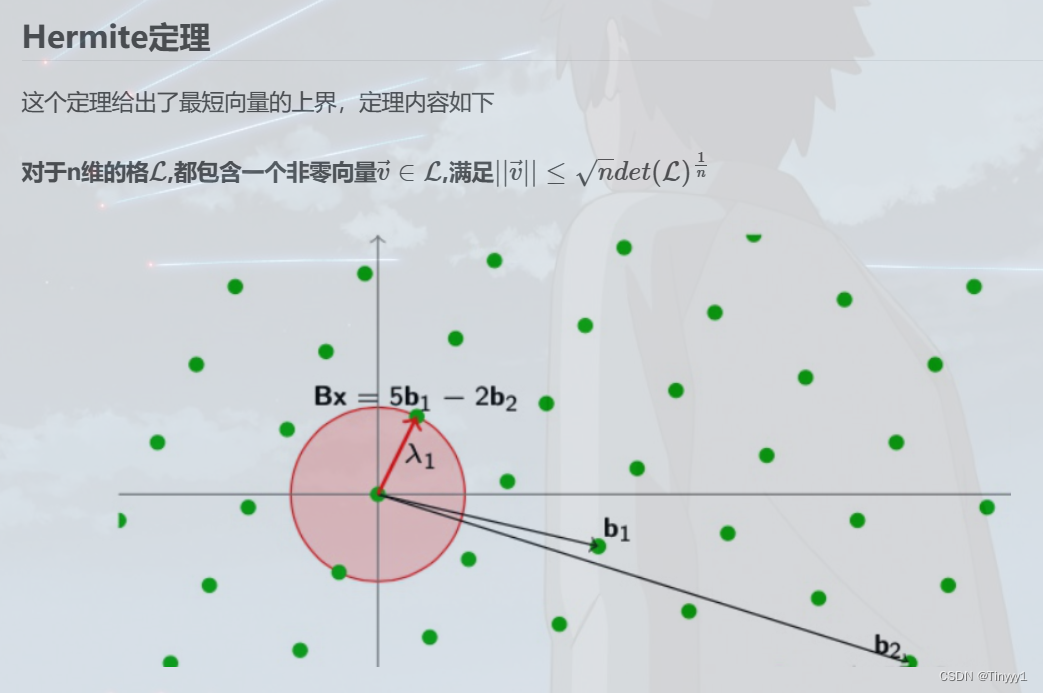
CVP问题
寻找最接近向量。
比如
C=(c1,....,cn)
D=(d1,...dn)
要求它俩之差的范数是最小的。
D-C=(d1-c1,...,dn-cn)
背包问题
背包问题定义:
假定一个背包可以承重S,现在有n个物品,其重量分别为a1,a2…an,试问装哪些物品可以恰好使得背包被装满,而且每个物品最多被装一次。转化成数学式子即是
x1a1+x2a2+...+xnan=S
其中xi=0或1
把明文flag表示成01的bit串,然后找到背包的一个私钥序列 a1....an,和私钥key,定义公钥n和
mi=ai*key mod n,ai满足超递增序列

比如明文flag=01110 , m=2,3,4,6,1
S = 2*0+3*1+4*1+6*1+1*0=13
构造格(每行都是向量)

知道S,知道m,如何求flag呢
构造一个等式:
怎么放到格子里去计算呢
(2*flag1,0,0...flag1*m1)
(2*flag1,2*flag2,...)=(2*flag1,2*flag2,...,S)
再减去最后一行向量
(2*flag1-1,2*flag2-1,...,S-S)=(2*flag1-1,2*flag2-1,...,0)
那么它的范数会变得很小
因为当flag=1的时候,元素值为1
flag=0的时候,元素值为-1
所以算它的LLL,很可能就是最短向量,也就是最终解。
代码实现一个背包问题如下:
from Crypto.Util.number import *
flag=b'Knaspack'
flag=bytes_to_long(flag)
flag=bin(flag)[2:] #转二进制
n=getPrime(100)
a=[getPrime(90)]
for i in range(len(flag)):
a.append(a[i]*2) #实现ai满足超递增序列
key=getPrime(50)
m=[]
for i in range(len(flag)):
m.append((a[i]*key)%n)
s=0
for i in range(len(flag)):
s+=m[i]*int(flag[i])
print('n=',n)
print('s=',s)
print('m=',m)exp:
from Crypto.Util.number import *
S= 11126794519526028436921421701917
M= [383762905355694917786587060709, 51830119385363629902016227441, 103660238770727259804032454882, 207320477541454519608064909764, 414640955082909039216129819528, 113586218839791872761101745079, 227172437679583745522203490158, 454344875359167491044406980316, 192994059392308776417656066655, 385988118784617552835312133310, 56280546243208899999466372643, 112561092486417799998932745286, 225122184972835599997865490572, 450244369945671199995730981144, 184793048565316194320304068311, 369586097130632388640608136622, 23476502935238571610058379267, 46953005870477143220116758534, 93906011740954286440233517068, 187812023481908572880467034136, 375624046963817145760934068272, 35552402601608085850710242567, 71104805203216171701420485134, 142209610406432343402840970268, 284419220812864686805681940536, 568838441625729373611363881072, 421981191925432541551569868167, 128266692524838877431981842357, 256533385049677754863963684714, 513066770099355509727927369428, 310437848872684813784696844879, 620875697745369627569393689758, 526055704164713049467629485539, 336415717003399893264101077101, 672831434006799786528202154202, 629967176687573367385246414427, 544238662049120529099334934877, 372781632772214852527511975777, 29867574218403499383866057577, 59735148436806998767732115154, 119470296873613997535464230308, 238940593747227995070928460616, 477881187494455990141856921232, 240066683662885774612555948487, 480133367325771549225111896974, 244571043325516892779065899971, 489142086651033785558131799942, 262588481976041365445105705907, 525176963952082730890211411814, 334658236578139256109264929651, 669316473156278512218529859302, 622937254986530818765901824627, 530178818647035431860645755277, 344661945968044658050133616577, 689323891936089316100267233154, 662952092546152426529376572331, 610208493766278647387595250685, 504721296206531089104032607393, 293746901087035972536907320809, 587493802174071945073814641618, 459291913022117684476471389259, 202888134718209163281784884541, 405776269436418326563569769082]
n = len(M)
L = matrix.zero(n + 1)
for row, x in enumerate(M):
L[row, row] = 2
L[row, -1] = x
L[-1, :] = 1
L[-1, -1] = S
res = L.LLL()
m = ''
for j in range(n + 1):
judge = res[j][:-1]
if set(judge).issubset([-1, 1]):
for i in res[j]:
if i == -1:
m += '1'
elif i == 1:
m += '0'
flag=int(m,2)
flag=long_to_bytes(flag)例题
NSSCTF [HNCTF 2022 WEEK2] ——littleLattice
题目
from Crypto.Util.number import *
from hashlib import *
p = getPrime(2048)
f = getPrime(1024)
g = getPrime(768)
h = pow(f,-1,p)*g%p
verify = sha256(bytes.fromhex(hex(f+g)[2:])).hexdigest()
print(f'verify = {verify}')
print(f'p = {p}')
print(f'h = {h}')
print('NSSCTF{' + md5(bytes.fromhex(hex(f+g)[2:])).hexdigest() + '}')
'''
verify = 24425b693dbcace08a32572d499a5cbeb36e30db9278704195c67c3d32a81bdf
p = 29908110980126088961686288727545150169450107297750996656924523214377817308111189721234667959695817050736874247951762130190209278324144437406652857446810518839546701950883392761869656586963587376306050382973323860395932741791372333809871487575268245618618143456971257992301722141464238875859134379745122404533776003095129169004284619647906206323263396219776072091827094295366090100037898314156271404760715453914459484087562963158208356228410105170495322276351631637885450926240143055767142216931354736779666836018983658010126520397012025067407223630891975504746697630878807952266767406899527721170062789607980517722293
h = 26523576589113781532769165293024254940419790396713708680496148398686334583553504180195363282085884580924842673123375450894537445679687851322807762432476357713740302064160599132450619363411158141423252170448770929403179895813409897048848337375715079396639330537231353596884530617911351334318435031007342479134081403319324838464987064025256038807217697133175585927493402963025439540077915248356077623612217525231722274634984400273765262532561558296870531741633238736650375250957780701118781183335729715295271752736307479795186963108377228330313771245434127095507278278768792281414702334956407755841000748255424212840137
'''
我们已知
要求flag,我们要求出f,g
我们的目标量就是f,g了
可以构造格
因为g,f的值小于已知的ℎ,p,而且||(f,g)||≈1024bit的大小小于≈
×1024bit
所以可以用LLL算法求解
exp:
from hashlib import sha256,md5
verify = "24425b693dbcace08a32572d499a5cbeb36e30db9278704195c67c3d32a81bdf"
p = 29908110980126088961686288727545150169450107297750996656924523214377817308111189721234667959695817050736874247951762130190209278324144437406652857446810518839546701950883392761869656586963587376306050382973323860395932741791372333809871487575268245618618143456971257992301722141464238875859134379745122404533776003095129169004284619647906206323263396219776072091827094295366090100037898314156271404760715453914459484087562963158208356228410105170495322276351631637885450926240143055767142216931354736779666836018983658010126520397012025067407223630891975504746697630878807952266767406899527721170062789607980517722293
h = 26523576589113781532769165293024254940419790396713708680496148398686334583553504180195363282085884580924842673123375450894537445679687851322807762432476357713740302064160599132450619363411158141423252170448770929403179895813409897048848337375715079396639330537231353596884530617911351334318435031007342479134081403319324838464987064025256038807217697133175585927493402963025439540077915248356077623612217525231722274634984400273765262532561558296870531741633238736650375250957780701118781183335729715295271752736307479795186963108377228330313771245434127095507278278768792281414702334956407755841000748255424212840137
Ge = Matrix(ZZ,[[1,h],[0,p]])
#print(Ge.LLL())
f,g = Ge.LLL()[0]
f,g = abs(f),abs(g)
if sha256(bytes.fromhex(hex(f+g)[2:])).hexdigest() == verify:
flag = 'NSSCTF{' + md5(bytes.fromhex(hex(f+g)[2:])).hexdigest() + '}'
print(flag)
为什么LLL算法可以得到我们需要的f’,g
LLL算法可以把(ℎ,1),(p,0)这组基,变成正交化程度最大的一组基,它可以求解最短向量问题
如果说点(f,g)正好是最短向量,那是不是用LLL算法就可以求解出f’,g的值
为什么点(f,g)是最短向量?
Hermite定理给出了最短向量的上界:
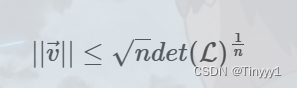
其行列式为p
所以最短向量||||≤
而p是2048bit的,g是768bit
所以向量v=(f,g)的长度||v||远小于的大小
所以可以认为我们需要求的f,g就是最短向量





















 329
329











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








