（java）三种方法求斐波那契数列的第n项

题目：写一个函数，输入n,求斐波那契数列的第n项。斐波那契数列的定义如下：

解答本题的方法有三：

• 按照定义编程，使用的方法是递归。
• 方法一递归分解的子问题存在大量的重复计算，于是我们将递归改为自上而下的循环实现。（本题的核心）
• 采用数学公式实现。

分析：

使用递归会有许多的重复计算：

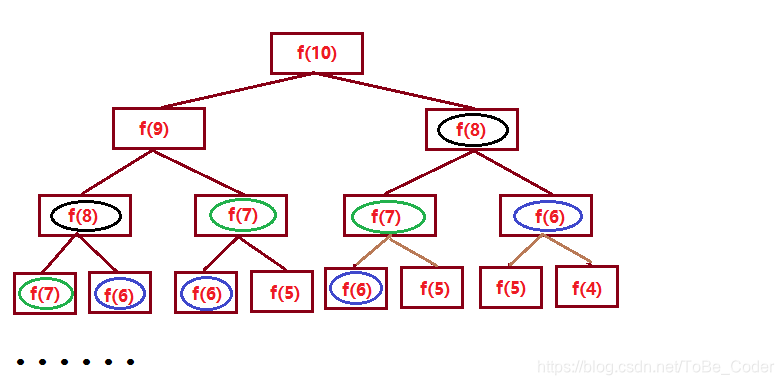
 方法三涉及到的数学公式：

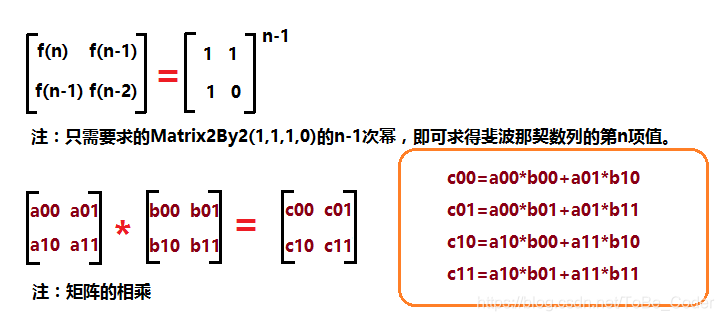
代码实现如下： 

package com.example.offer;

/**
 *          0  n=0
 * f(n)=    1  n=1
 *          f(n-1)+f(n-2)  n>1
 */
public class FibonacciTest {

    public static void main(String[] args) {
       for (int i = 0; i < 10; i++) {
            System.out.println("方法一："+fibonacci01(i));
            System.out.println("方法二："+fibonacci02(i));
            System.out.println("方法三："+fibonacci03(i));
        }
    }
    /**
     *  简单的实现  递归的实现存在很多的重复计算
     * @param n 求第n个斐波那锲数
     * @return
     */
    public static long fibonacci01(long n){
        if(n<=0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        return fibonacci01(n-1)+ fibonacci01(n-2);
    }

    /**
     *  将递归的实现转为循环  时间复杂度为O(n)
     * @param n 求第n个斐波那锲数
     * @return
     */
    public static long fibonacci02(long n) {
        if(n<=0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        long fibNMinusOne=1;//n-1
        long fibNMInusTwo=0;//n-2
        long fibN=0;
        for (int i = 2; i <= n; i++) {
            fibN=fibNMinusOne+fibNMInusTwo;

            fibNMInusTwo=fibNMinusOne;
            fibNMinusOne=fibN;
        }
        return fibN;
    }

    /**
     * 采用数学公式
     * --                 --            --      -- (n-1)
     * \   f（n）   f(n-1) \      =     \  1  1  \
     * \   f(n-1)   f(n+1) \            \  1  0  \
     * --                  --           --      --
     * 由此可知，我们只需要计算后面矩阵的值 即可以知道 f(n)的值
     * @return
     */
    public static long fibonacci03(int n){
        int[] result={0,1};
        if(n<2){
            return result[n];
        }
        //当大于2的情况
        Matrix2By2 powerNMinus2=matrixPower(n-1);
        return powerNMinus2.m_00;
    }

    /**
     * 计算矩阵Matrix2By2(1,1,1,0)的n次方
     * @param n
     * @return
     */
    public static Matrix2By2 matrixPower(long n){
        //分三种情况 n=1;n为偶数；n为奇数
        Matrix2By2 matrix=null;
        if(n==1){ //n为1
            matrix=new Matrix2By2(1,1,1,0);
        }else if(n%2==0){ //n为偶数
            matrix=matrixPower(n/2);
            matrix=matrixMultiply(matrix,matrix);
        }else if(n%2==1){//n为奇数
            matrix=matrixPower((n-1)/2);
            matrix=matrixMultiply(matrix,matrix);
            matrix=matrixMultiply(matrix,new Matrix2By2(1,1,1,0));
        }
        return matrix;
    }

    /**
     * 两个矩阵相乘
     * @return
     */
    public static Matrix2By2 matrixMultiply(Matrix2By2 matrix1,Matrix2By2 matrix2){
        return new Matrix2By2(
                matrix1.m_00*matrix2.m_00+matrix1.m_01*matrix2.m_10,
                matrix1.m_00*matrix2.m_01+matrix1.m_01*matrix2.m_11,
                matrix1.m_10*matrix2.m_00+matrix1.m_11*matrix2.m_10,
                matrix1.m_10*matrix2.m_01+matrix1.m_11*matrix2.m_11
        );
    }
}

/**
 *  2*2的矩阵
 */
class Matrix2By2{
    //一个2*2的矩阵 有4个元素
    public long m_00;
    public long m_01;
    public long m_10;
    public long m_11;

    public Matrix2By2(){

    }
    public Matrix2By2(long m_00,long m_01,long m_10,long m_11){
        this.m_00=m_00;
        this.m_01=m_01;
        this.m_10=m_10;
        this.m_11=m_11;
    }
}

时间复杂度分析：方法一计算量随着n的增大急剧增大，时间复杂度是以n的指数递增，时间复杂度为O(2^n);方法二采用自上而下的循环，时间复杂度为O(n),性能比方法一大大优化，是此题的核心解法；第三种方法使用数学函数，时间复杂度为O(logn)。但是代码比较复杂，时间常数较大，此方法做了解即可，软件中使用较少。