题目大意:有一些化合物,每个化合物都由两种元素组成的,然后你按照顺序依次把一些简单化合物装到车上,但这里存在一个安全隐患:如果车上存在k个简单化合物,正好包含k种元素,那么它就将组成一个易爆的混合物,为了安全起见,每当你拿到一个化合物,正好包含k中元素,那么它们将组成一个易爆的混合物,为了安全起见,每当你拿到一个混合物时,如果它和已装车的化合物形成易爆混合物,你就应当拒绝装车,否则就装车,编程输出有多少个没有装车的化合物。
题目分析:刘汝佳书上说是把每个元素都看成一个顶点,则一个简单化合物就是一条边,当整个图存在环的时候,组成环的边对应的化合物是危险的,反之则是安全的。这样,我们可以用一个并查集来维护图的联通分量集合,每次得到一个简单化合物(x,y)时检查x和y是否在同一个集合中。如果是,则拒绝,反之则接受。
刚开始不是很理解为什么非要是当整个图存在环的时候对应的化合物危险,后来想到,既然一个简单化合物就是一条边,而顶点是元素,那么当成环的时候,即顶点和边都相同,即满足题目条件存在k个简单化合物,正好包含k种元素。然后就是并查集的问题,以前 没有接触过,然后趁机学习了一番,找到了一位大佬的博客,大佬指向了一个更大佬的博客,现在我把这两位大佬的都拿过来。。。
恩,先把我自己这题的代码贴上。
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
const int maxn = 100000+10;
int pa[maxn];
int find(int x){
if(pa[x] == x)
return x;
else{
int r;
r=pa[x];
while( pa[r] != r)
r=pa[r];
return r;
}
}
int main(){
int x,y;
while(scanf("%d",&x)==1){
for(int i=0;i<=maxn;i++)
pa[i] = i;
int count =0;
while( x != -1){
scanf("%d",&y);
x=find(x);y=find(y);
if(x==y)
count++;
else pa[x]=y;
scanf("%d",&x);
}
printf("%d\n",count);
}
return 0;
}
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
使用并查集时,首先会存在一组不相交的动态集合 S={S 1 ,S 2 ,⋯,S k } ,一般都会使用一个整数表示集合中的一个元素。
每个集合可能包含一个或多个元素,并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的,具体选择哪个元素作为代表一般也是不关心的。我们关心的是,对于给定的元素,可以很快的找到这个元素所在的集合(的代表),以及合并两个元素所在的集合,而且这些操作的时间复杂度都是常数级的。
并查集的基本操作有三个:
- makeSet(s):建立一个新的并查集,其中包含 s 个单元素集合。
- unionSet(x, y):把元素 x 和元素 y 所在的集合合并,要求 x 和 y 所在的集合不相交,如果相交则不合并。
- find(x):找到元素 x 所在的集合的代表,该操作也可以用于判断两个元素是否位于同一个集合,只要将它们各自的代表比较一下就可以了。
并查集的实现原理也比较简单,就是使用树来表示集合,树的每个节点就表示集合中的一个元素,树根对应的元素就是该集合的代表,如图 1 所示。

图 1 并查集的树表示
图中有两棵树,分别对应两个集合,其中第一个集合为 {a,b,c,d} ,代表元素是 a ;第二个集合为 {e,f,g} ,代表元素是 e 。
树的节点表示集合中的元素,指针表示指向父节点的指针,根节点的指针指向自己,表示其没有父节点。沿着每个节点的父节点不断向上查找,最终就可以找到该树的根节点,即该集合的代表元素。
现在,应该可以很容易的写出 makeSet 和 find 的代码了,假设使用一个足够长的数组来存储树节点(很类似之前讲到的静态链表),那么 makeSet 要做的就是构造出如图 2 的森林,其中每个元素都是一个单元素集合,即父节点是其自身:

图 2 构造并查集初始化
相应的代码如下所示,时间复杂度是 O(n) :
接下来,就是 find 操作了,如果每次都沿着父节点向上查找,那时间复杂度就是树的高度,完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。
路径压缩,就是在每次查找时,令查找路径上的每个节点都直接指向根节点,如图 3 所示。

图 3 路径压缩
我准备了两个版本的 find 操作实现,分别是递归版和非递归版,不过两个版本目前并没有发现有什么明显的效率差距,所以具体使用哪个完全凭个人喜好了。
最后是合并操作 unionSet,并查集的合并也非常简单,就是将一个集合的树根指向另一个集合的树根,如图 4 所示。

图 4 并查集的合并
这里也可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界,在合并时,总是将具有较小秩的树根指向具有较大秩的树根。简单的说,就是总是将比较矮的树作为子树,添加到较高的树中。为了保存秩,需要额外使用一个与 uset 同长度的数组,并将所有元素都初始化为 0。
下面是按秩合并的并查集的完整代码,这里只包含了递归的 find 操作。
除了按秩合并,并查集还有一种常见的策略,就是按集合中包含的元素个数(或者说树中的节点数)合并,将包含节点较少的树根,指向包含节点较多的树根。这个策略与按秩合并的策略类似,同样可以提升并查集的运行速度,而且省去了额外的 rank 数组。
这样的并查集具有一个略微不同的定义,即若 uset 的值是正数,则表示该元素的父节点(的索引);若是负数,则表示该元素是所在集合的代表(即树根),而且值的相反数即为集合中的元素个数。相应的代码如下所示,同样包含递归和非递归的 find 操作:
如果要获取某个元素 x 所在集合包含的元素个数,可以使用 -uset[find(x)] 得到。
并查集的空间复杂度是 O(n) 的,这个很显然,如果是按秩合并的,占的空间要多一些。find 和 unionSet 操作都可以看成是常数级的,或者准确来说,在一个包含 n 个元素的并查集中,进行 m 次查找或合并操作,最坏情况下所需的时间为 O(mα(n)) ,这里的 α 是 Ackerman 函数的某个反函数,在极大的范围内(比可观察到的宇宙中估计的原子数量 10 80 还大很多)都可以认为是不大于 4 的。具体的时间复杂度分析,请参见《算法导论》的 21.4 节 带路径压缩的按秩合并的分析。
作者:CYJB
出处:http://www.cnblogs.com/cyjb/
GitHub:https://github.com/CYJB/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
为了解释并查集的原理,我将举一个更有爱的例子。 话说江湖上散落着各式各样的大侠,有上千个之多。他们没有什么正当职业,整天背着剑在外面走来走去,碰到和自己不是一路人的,就免不了要打一架。但大侠们有一个优点就是讲义气,绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”,只要是能通过朋友关系串联起来的,不管拐了多少个弯,都认为是自己人。这样一来,江湖上就形成了一个一个的群落,通过两两之间的朋友关系串联起来。而不在同一个群落的人,无论如何都无法通过朋友关系连起来,于是就可以放心往死了打。但是两个原本互不相识的人,如何判断是否属于一个朋友圈呢?
我们可以在每个朋友圈内推举出一个比较有名望的人,作为该圈子的代表人物,这样,每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”……两人只要互相对一下自己的队长是不是同一个人,就可以确定敌友关系了。
但是还有问题啊,大侠们只知道自己直接的朋友是谁,很多人压根就不认识队长,要判断自己的队长是谁,只能漫无目的的通过朋友的朋友关系问下去:“你是不是队长?你是不是队长?”这样一来,队长面子上挂不住了,而且效率太低,还有可能陷入无限循环中。于是队长下令,重新组队。队内所有人实行分等级制度,形成树状结构,我队长就是根节点,下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候,只要一层层向上问,直到最高层,就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否连通,至于他们是如何连通的,以及每个圈子内部的结构是怎样的,甚至队长是谁,并不重要。所以我们可以放任队长随意重新组队,只要不搞错敌友关系就好了。于是,门派产生了。
http://i3.6.cn/cvbnm/6f/ec/f4/1e9cfcd3def64d26ed1a49d72c1f6db9.jpg
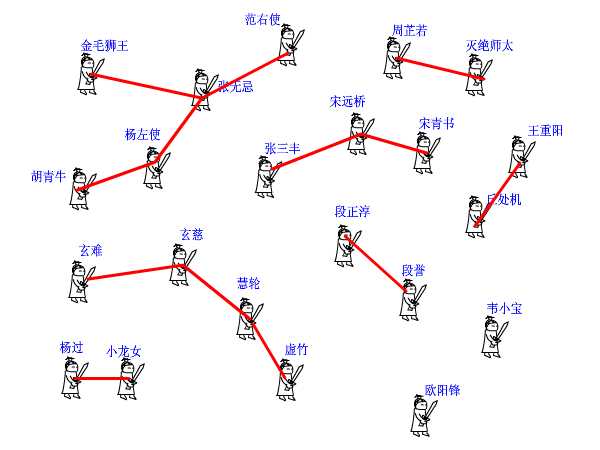
下面我们来看并查集的实现。 int pre[1000]; 这个数组,记录了每个大侠的上级是谁。大侠们从1或者0开始编号(依据题意而定),pre[15]=3就表示15号大侠的上级是3号大侠。如果一个人的上级就是他自己,那说明他就是掌门人了,查找到此为止。也有孤家寡人自成一派的,比如欧阳锋,那么他的上级就是他自己。每个人都只认自己的上级。比如胡青牛同学只知道自己的上级是杨左使。张无忌是谁?不认识!要想知道自己的掌门是谁,只能一级级查上去。 find这个函数就是找掌门用的,意义再清楚不过了(路径压缩算法先不论,后面再说)。
int find(int x) //查找我(x)的掌门
{
int r=x; //委托 r 去找掌门
while (pre[r ]!=r) //如果r的上级不是r自己(也就是说找到的大侠他不是掌门 = =)
r=pre[r ] ; // r 就接着找他的上级,直到找到掌门为止。
return r ; //掌门驾到~~~
}
再来看看join函数,就是在两个点之间连一条线,这样一来,原先它们所在的两个板块的所有点就都可以互通了。这在图上很好办,画条线就行了。但我们现在是用并查集来描述武林中的状况的,一共只有一个pre[]数组,该如何实现呢? 还是举江湖的例子,假设现在武林中的形势如图所示。虚竹小和尚与周芷若MM是我非常喜欢的两个人物,他们的终极boss分别是玄慈方丈和灭绝师太,那明显就是两个阵营了。我不希望他们互相打架,就对他俩说:“你们两位拉拉勾,做好朋友吧。”他们看在我的面子上,同意了。这一同意可非同小可,整个少林和峨眉派的人就不能打架了。这么重大的变化,可如何实现呀,要改动多少地方?其实非常简单,我对玄慈方丈说:“大师,麻烦你把你的上级改为灭绝师太吧。这样一来,两派原先的所有人员的终极boss都是师太,那还打个球啊!反正我们关心的只是连通性,门派内部的结构不要紧的。”玄慈一听肯定火大了:“我靠,凭什么是我变成她手下呀,怎么不反过来?我抗议!”抗议无效,上天安排的,最大。反正谁加入谁效果是一样的,我就随手指定了一个。这段函数的意思很明白了吧?
void join(int x,int y) //我想让虚竹和周芷若做朋友
{
int fx=find(x),fy=find(y); //虚竹的老大是玄慈,芷若MM的老大是灭绝
if(fx!=fy) //玄慈和灭绝显然不是同一个人
pre[fx ]=fy; //方丈只好委委屈屈地当了师太的手下啦
}






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








