POJ 2409 Let it Bead（polya）

Description
用m种颜色给长度为n的项链染色，旋转和翻转相同算同一种方案，问一共有多少种不同的方案
Input
每组用例占一行为两个整数m和n表示颜色数和项链长度，以0 0结束输入
Output
对于每组用例，输出染色方案数
Sample Input
1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0
Sample Output
1
2
3
5
8
13
21
Solution
polya，先考虑旋转，有n种置换，旋转k个元素后循环节即轮换数为gcd(k,n)，故方案数为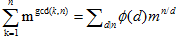，然后是翻转，对称轴显然为直径，当n为偶数时有两种对称轴，一种过两点，另一种过两个中点，第一种对称轴有n/2个，翻转180度的轮换数为n/2+1，第二种对称轴也有n/2个，翻转180度的轮换数为n/2，方案数为n/2*m^(n/2)+n/2*m^(n/2+1)；当n为奇数时对称轴只有一种，即过一点以及一个中点，共n个，翻转180度的轮换数为n/2，方案数为n*m^(n/2)，所以翻转也有n种置换，总置换数为2*n。
Code

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
int gcd(int a,int b)
{
    if(b==0)return a;
    return gcd(b,a%b);
}
int main()
{
    int n,m;
    while(~scanf("%d%d",&m,&n),n||m)
    {
        int ans=0;
        for(int i=1;i<=n;i++)
            ans+=pow(1.0*m,1.0*gcd(i,n));
        if(n&1)ans+=n*pow(1.0*m,1.0*(n/2+1));
        else ans+=n/2*pow(1.0*m,1.0*n/2)+n/2*pow(1.0*m,1.0*(n/2+1));
        ans/=2*n;
        printf("%d\n",ans);
    }
    return 0;
}