HDU 5779 Tower Defence(????)

Description
小白最近痴迷于玩Tower Defence。他想要自己制作一张地图。地图是一张有n个点的无向图（图可以不连通,没有重边和自环），所有边的长度都为1，满足从1号点到其他任意一个点的最短路都不等于k.小白想知道这样的图有多少个。如果两个顶点不连通，那么它们之间的距离为无穷大
Input
第一行输入一个整数T（1≤T≤10)
每组数据有一行，有两个整数n和k(1≤k,n≤60)
Output
对于每组数据，输出一行，图的个数，显然很大，对1e9+7取模
Sample Input
3
3 2
4 2
5 3
Sample Output
6
28
808
Solution
用dp[i][j][k]表示包含1点的连通块点数为j，连通块中点到1的最短路最大值为i，连通块中有k个点到1的最短路长度为i的方法数，那么有转移方程

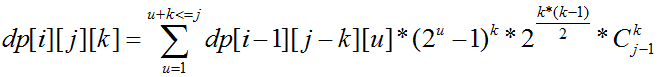
解释下转移方程，从dp[i-1][j-k][u]到dp[i][j][k]，要将k个点插进一个最短路长度为i-1的图中且插入的每个点到1点最短路为i，那么这k个点只能插在与1的最短路为i-1的u个点上，每个点插入的方案是(2^u-1)种，k个点就是(2^u-1)^k，而这新加入的k个点之间可以随便连边，有2^((k*(k-1)/2)种方案，最后是从连通块中选出k个点使其与1的最短路为i，方案数是C(j-1,k)（1点到自身距离不为i），在求出所有的dp[i][j][k]后，每次要从n-1个点中选取i-1个点与1点组成这个连通块，方案数C(n-1,i-1)，这个连通块处理好后，剩下n-i个点可以随便连边，方案数2^((n-i)*(n-i-1)/2)，所以最后的答案就是

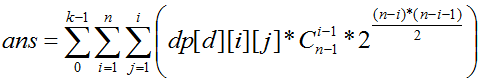
Code

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
#define mod 1000000007ll
#define maxn 66
ll C[maxn][maxn],f[maxn][maxn],g[maxn*maxn],dp[maxn][maxn][maxn];
void init()
{
    memset(C,0,sizeof(C));
    memset(f,0,sizeof(f));
    memset(dp,0,sizeof(dp));
    g[0]=1;
    for(int i=1;i<maxn*maxn;i++)g[i]=g[i-1]*2%mod;
    for(int i=0;i<maxn;i++)
    {
        C[i][0]=C[i][i]=1;
        for(int j=1;j<i;j++)C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
    }
    for(int i=1;i<maxn;i++)
    {
        f[i][0]=1;
        for(int j=1;j<maxn;j++)f[i][j]=f[i][j-1]*(g[i]-1)%mod;
    }
    dp[0][1][1]=1;
    for(int i=1;i<maxn;i++)
        for(int j=i;j<maxn;j++)
            for(int k=1;k<=j;k++)
                for(int u=1;u+k<=j;u++)
                {
                    dp[i][j][k]+=dp[i-1][j-k][u]*f[u][k]%mod*g[k*(k-1)/2]%mod*C[j-1][k]%mod;
                    dp[i][j][k]%=mod;
                }
}
int main()
{
    init();
    int T,k,n;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&k);
        ll ans=0;
        for(int d=0;d<k;d++)
            for(int i=1;i<=n;i++)
                for(int j=1;j<=i;j++)
                    ans+=dp[d][i][j]*C[n-1][i-1]%mod*g[(n-i)*(n-i-1)/2]%mod,ans%=mod;
        printf("%I64d\n",ans);
    }
    return 0;
}