Description
给出一个序列Ai,可以让每个Ai异或上一个x使得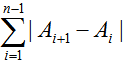
Input
第一行一整数T表示用例组数,每组用例首先输入序列长度n,之后n个整数Ai表示该序列(T<=20,0<=Ai<2^20,1<=n<=10^5)
Output
对于每组用例,输出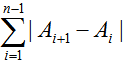
Sample Input
2
3
0 3 0
3
1 3 1
Sample Output
1 2
0 4
Solution
看见异或考虑拆位,对于两个数来说,A[i]和A[i+1]同时异或一个x,其二进制表示中相同的位做差值仍为0,故之后只考虑不同的位,最后两者做完差后的值主要看两者最高位谁是1,例如第i位是最高位,那么这一位对答案的贡献必然是2^i,而一个较低位j对答案的贡献需要看x的第j位和第i位是否相同,相同则为其本来的贡献,不同则需加个负号,例如第一个数第i为是1,第j位是0,第二个数第i为是0,第j位是1,那么这异或前这两位的贡献分别是2^i和-2^j,而异或后,第i位贡献依旧是2^i,第j位的贡献取决于x第i位和第j位是否相同,相同就还是-2^j,不相同就是2^j,于是对这n-1对数做以上处理,先将对应位在异或前的贡献存在一个20*20的矩阵中,之后2^20枚举x每一位,通过dfs+剪枝得到最小值以及使得值最小的最小x值
Code
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
#define maxn 111111
int T,n,a[maxn],deep,x;
ll num[22][22],ans;
void dfs(int pos,ll sum,int cnt)
{
if(pos==deep+1)
{
if(sum<ans)ans=sum,x=cnt;
else if(sum==ans)x=min(x,cnt);
return ;
}
if(sum>ans)return ;
for(int i=0;i<2;i++)
{
ll temp_sum=sum+num[pos][pos];
for(int j=0;j<pos;j++)
if(((cnt>>j)&1)==i)temp_sum+=num[pos][j];
else temp_sum-=num[pos][j];
dfs(pos+1,temp_sum,cnt+(i<<pos));
}
}
int main()
{
scanf("%d",&T);
while(T--)
{
ans=deep=0;
memset(num,0,sizeof(num));
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<n;i++)
{
int ta=max(a[i],a[i+1]),tb=min(a[i],a[i+1]);
ans+=ta-tb;
int high=19;
while(high>=0&&~((ta^tb)>>high)&1)high--;
deep=max(deep,high);
for(int j=high;j>=0;j--)
num[high][j]+=(ta>>j&1)-(tb>>j&1);
}
for(int i=0;i<=deep;i++)
for(int j=0;j<=i;j++)
num[i][j]<<=j;
dfs(0,0,0);
printf("%d %I64d\n",x,ans);
}
return 0;
}























 146
146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








