文章目录
一、栈接口与实现
1.操作与接口
-
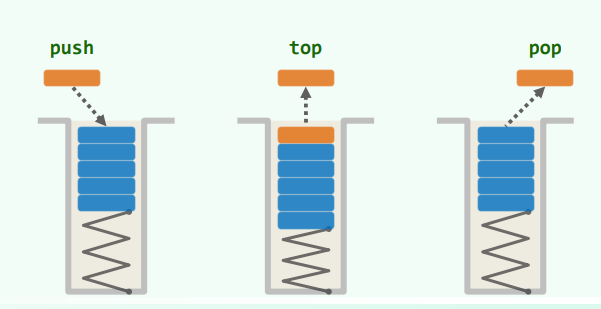
栈(stack)是受限的序列
- 只能在栈顶(top)插入和删除
- 栈底(bottom)为盲端
-
基本接口
- size() / empty()
- push() 入栈
- pop() 出栈
- top() 查顶
-
后进先出(LIFO),先进后出(FILO)
2.实例

3.代码
template <typename T> class Stack: public Vector<T> {
public: //原有接口一概沿用
void push( T const & e ) { insert( e ); } //入栈
T pop() { return remove( size() – 1 ); } //出栈
T & top() { return (*this)[ size() – 1 ]; } //取顶
};
- 如此实现的栈各接口,均只需O(1)时间
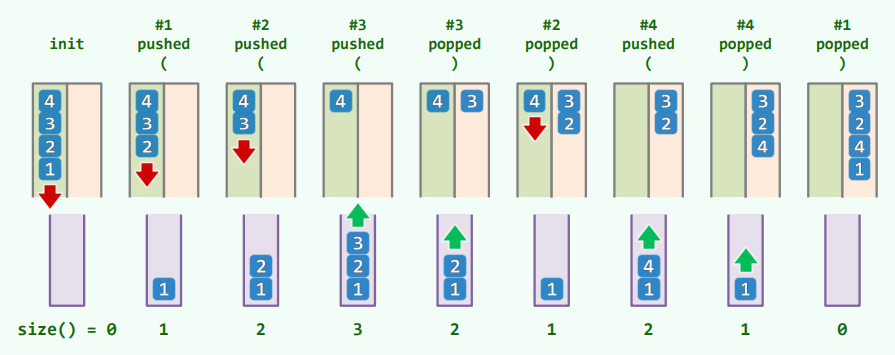
二、调用栈
1.实例
hailstone(int n) {
if ( 1 < n )
n % 2 ? odd( n ) : even( n );
}
even( int n ) { hailstone( n / 2 ); }
odd( int n ) { hailstone( 3*n + 1 ); }
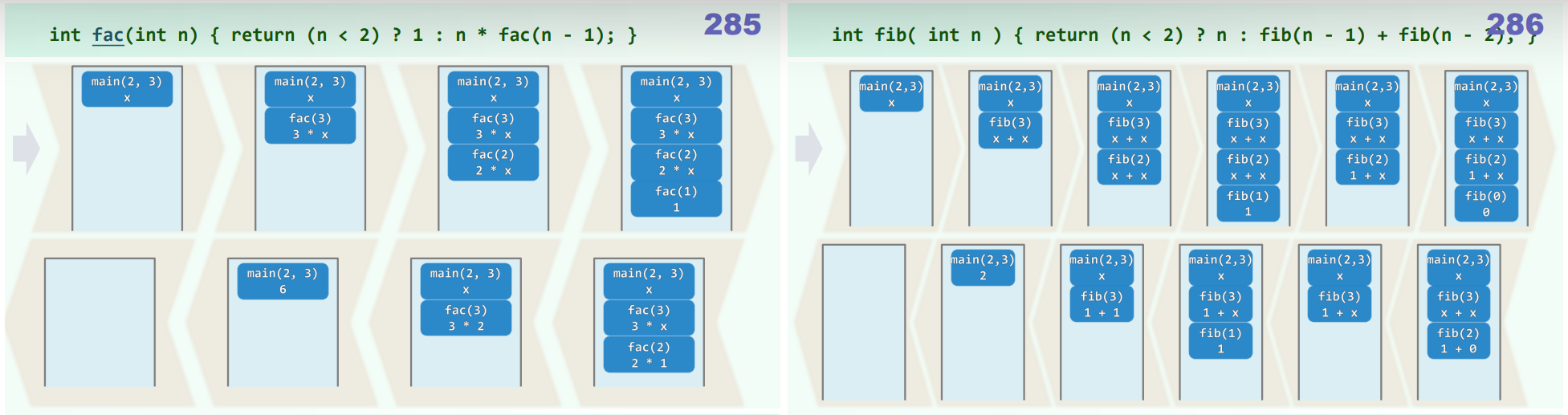
2.消除递归
2.1 动机+方法
-
递归函数的空间复杂度
- 主要取决于最大递归深度
- 而非递归实例总数
-
为隐式地维护调用栈需花费额外的时间、空间
-
为节省空间,可显式地维护调用栈或者将递归算法改写为迭代版本
2.2 实例

- 通常,消除递归只是在常数意义上优化空间
void hailstone( int n ) { //O(1)空间
while ( 1 < n )
n = n % 2 ? 3*n + 1 : n/2;
}
int fib( int n ) { //O(1)空间
int f = 0, g = 1;
while ( 0 < n-- ) {
g += f; f = g - f;
}
return f;
}
int fac( int n ) {
int f = 1; //O(1)空间
while ( n > 1 )
f *= n--;
return f;
}
3.尾递归
3.1 尾递归:在递归实例中,作为最后一步的递归调用
fac(n) {
if (1 > n) return 1; //base
return n * fac( n-1 ); //tail recursion
}
3.2 性质
-
系最简单的递归模式
-
一旦抵达递归基,便会引发一连串的return (且返回地址相同), 调用栈相应地连续pop
-
故不难改写为迭代形式
-
越来越多的编译器可以 自动识别并代为改写
-
时间复杂度有常系数改进 空间复杂度或有渐近改进
3.3 消除
fac(n) { //尾递归
if (1 > n) return 1;
return n * fac( n-1 );
} //O(n)时间 + O(n)空间
fac(n) { //统一转换为迭代
int f = 1; //记录子问题的解
next: //转向标志,模拟递归调用
if (1 > n) return f;
f *= n--;
goto next; //模拟递归返回
} //O(n)时间 + O(1)空间
fac(n) { //简捷
int f = 1;
while (1 < n) f *= n--;
return f;
} //O(n)时间 + O(1)空间
三、进制转换
-
若使用向量,则扩容策略必须得当;若使用列表,则多数接口均被闲置
-
使用栈,既可满足以上要求,亦可有效控制计算成本
void convert( Stack & S, __int64 n, int base ) {
char digit[] = "0123456789ABCDEF"; //数位符号,如有必要可相应扩充
while ( n > 0 ) //由低到高,逐一计算出新进制下的各数位 {
S.push( digit[ n % base ] );
n /= base;
} //余数入栈,n更新为除商
} //新进制下由高到低的各数位,自顶而下保存于栈S中
main() {
Stack S; convert( S, n, base ); //用栈记录转换得到的各数位
while ( ! S.empty() ) printf( "%c", S.pop() ); //逆序输出
}
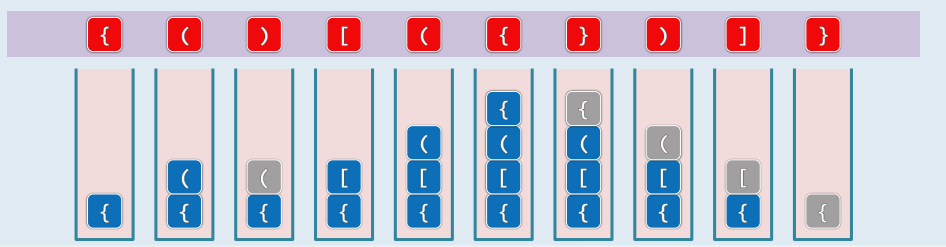
四、括号匹配
1.实例
2.构思:由内而外
- 顺序扫描表达式,用栈记录已扫描的部分(实际上只需记录左括号)
- 反复迭代:凡遇"(“,则进栈;凡遇”)",则出栈
3.代码
bool paren( const char exp[], int lo, int hi ) {
Stack<char> S; //使用栈记录已发现但尚未匹配的左括号
for ( int i = lo; i < hi; i++ )
if ( '(' == exp[i] ) S.push( exp[i] ); //遇左括号:则进栈
else if 拓展:多类括号
( ! S.empty() ) S.pop(); //遇右括号:若栈非空,则弹出对应的左括号
else return false; //否则(遇右括号时栈已空),必不匹配
return S.empty(); //最终栈空,当且仅当匹配 实现
}
4.实例:一种括号
- 实际上,若仅考虑一种括号,只需一个计数器足矣:S.size()
- 一旦转负,则为失配(右括号多余);最后归零,即为匹配(否则左括号多余)
5.拓展:多类括号
五、栈混洗
1.栈混洗
-
考查栈A=< a 1 , a 2 , a 3 , . . . , a n a_1,a_2,a_3,...,a_n a1,a2,a3,...,an],B=S=∅;只允许将 A 的顶元素弹出并压入 S ,或将 S 的顶元素弹出并压入 B,亦即S.push(A.pop()),B.push(S.pop())
-
若经一系列以上操作后,A中元素全部转入B中,即B=[ a k 1 , a a k 2 , . . . , a k n a_{k1},a_{ak2},...,a_{kn} ak1,aak2,...,akn>,则称为A的一个栈混洗
2.计数(SP(n))
- 一般地,对于长度为n的序列,混洗总数SP(n) =n!
- 考查S再度变空(A首元素从S中弹出)的时刻,无非n种情况:
S P ( n ) = ∑ k = 1 n S P ( k − 1 ) ⋅ S P ( n − k ) = c a t a l a n ( n ) = ( 2 n ) ! ( n + 1 ) ! ⋅ n SP(n)=\sum_{k=1}^{n}SP(k-1)·SP(n-k)=catalan(n)=\frac{(2n)!}{(n+1)!·n} SP(n)=∑k=1nSP(k−1)⋅SP(n−k)=catalan(n)=(n+1)!⋅n(2n)!
3.甄别
3.1 检测禁形
-
任意三个元素能否按某相对次序出现于混洗中,与其它元素无关
-
禁形:对任何1 ≤i < j < k ≤ n,[ …, k , …, i , …, j , … > 必非栈混洗
3.2 直接模拟
-
O( n 3 n^3 n3)的甄别算法:[ p1, p2, p3, …, pn >是< 1, 2, 3, …, n ]的栈混洗,当且仅当 对于任意i < j,不含模式[ …, j+1, …, i, …, j, … >
-
O(n)算法:直接借助栈A、B和S,模拟混洗过程。每次S.pop()之前,检测S是否已空;或需弹出的元素在S中,却非顶元素
4.括号匹配
- 每一栈混洗,都对应于栈S的n次push与n次pop操作构成的某一序列;反之亦然
- n个元素的栈混洗,等价于n对括号的匹配;二者的组合数,也自然相等
六、中缀表达式求值
1.问题与构思
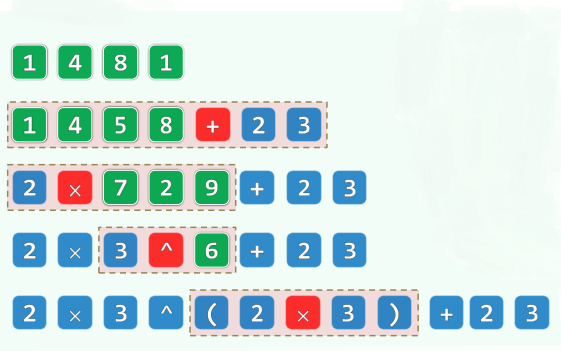
1.1 减而治之
- 优先级高的局部执行计算,并被代以其数值运算符渐少,直至得到最终结果
-
str(v):数值v对应的字符串(名);val(S):符号串S对应的数值(实)
-
设表达式: S = S L + S 0 + S R 设表达式:S = S_L + S_0 + S_R 设表达式:S=SL+S0+SR
- S 0 可优先计算,且 v a l ( S 0 ) = v 0 S_0可优先计算,且val(S_0) = v_0 S0可优先计算,且val(S0)=v0
-
则有递推化简关系 v a l ( S ) = v a l ( S L + s t r ( v 0 ) + S R ) val(S) = val( S_L + str(v_0) + S_R) val(S)=val(SL+str(v0)+SR)
1.2 优先级(如何高效地找到可优先计算的 S 0 S_0 S0(亦即,其对应的运算符))
-
与括号匹配迭代版类似,但亦不尽相同,不能简单地按“左先右后”次序处理各运算符
-
约定俗成的优先级:1+2*3^4
-
可强行改变次序的括号:(((1+2)*3)^4)
1.3 延迟缓存
-
仅根据表达式的前缀,不足以确定各运算符的计算次序只有获得足够的后续信息,才能确定其中哪些运算符可以执行
-
体现在求值算法的流程上 为处理某一前缀,必须提前预读并分析更长的前缀
,为此,需借助某种支持延迟缓冲的机制
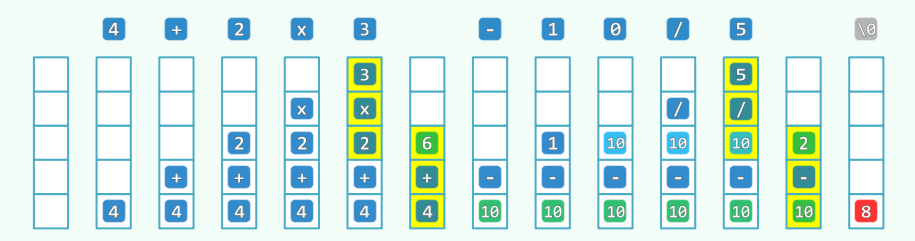
1.4 求值算法 = 栈 + 线性扫描
- 自左向右扫描表达式,用栈记录已扫描的部分(含已执行运算的结果)
-
栈的顶部存在可优先计算的子表达式
-
? 该子表达式退栈;计算其数值;计算结果进栈
-
: 当前字符进栈,转入下一字符
-
- 只要语法正确,则栈内最终应只剩一个元素
2.算法
2.1 主算法
double evaluate( char* S, char* RPN ) { //S保证语法正确
Stack opnd; Stack optr; //运算数栈、运算符栈
optr.push('\0'); //哨兵
while ( ! optr.empty() ) { //逐个处理各字符,直至运算符栈空
if ( isdigit( *S ) ) //若为操作数(可能多位、小数),则
readNumber( S, opnd ); //读入
else //若为运算符,则视其与栈顶运算符之间优先级的高低
switch( priority( optr.top(), *S ) ) { /* 分别处理 */ }
}
return opnd.pop(); //弹出并返回最后的计算结果
}
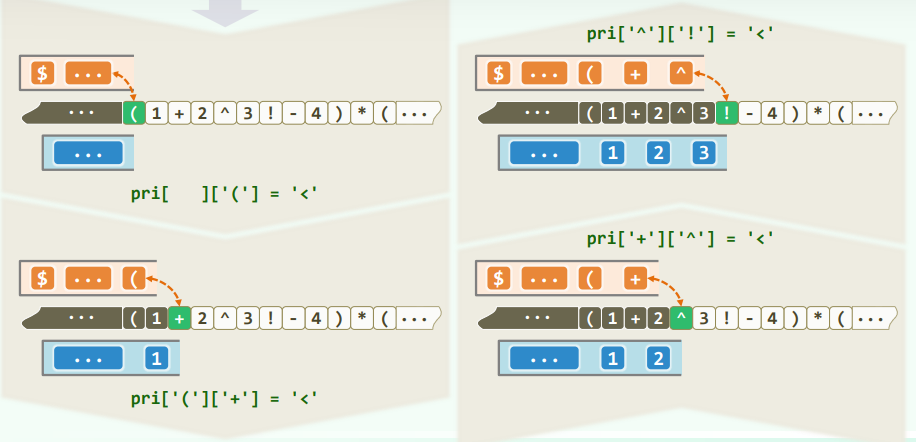
2.2 优先级表
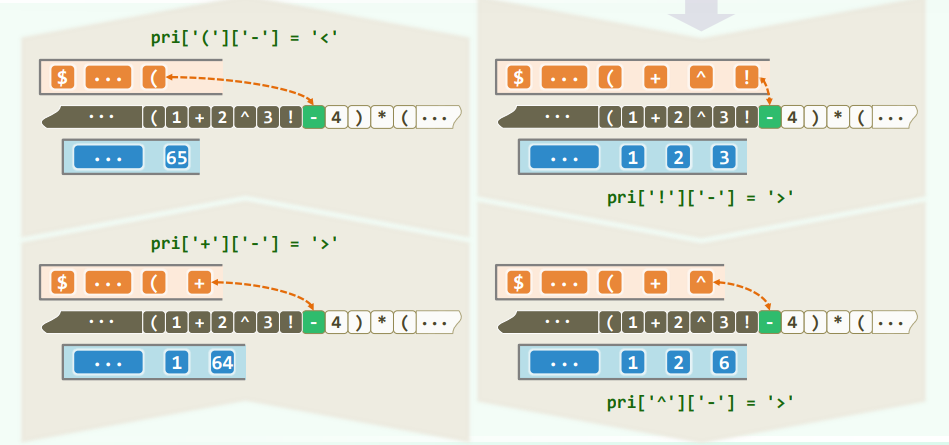
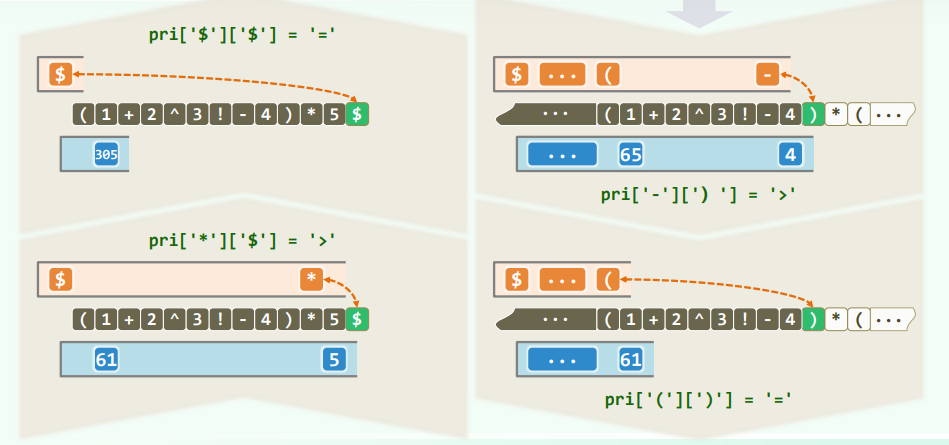
const char pri[N_OPTR][N_OPTR] = { //运算符优先等级 [栈顶][当前]
/* -- + */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* | - */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* 栈 * */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 顶 / */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 运 ^ */ '>', '>', '>', '>', '>', '<', '<', '>', '>',
/* 算 ! */ '>', '>', '>', '>', '>', '>', ' ', '>', '>',
/* 符 ( */ '<', '<', '<', '<', '<', '<', '<', '=', ' ',
/* | ) */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* -- \0 */ '<', '<', '<', '<', '<', '<', '<', ' ', '='
// + - * / ^ ! ( ) \0
// |-------------- 当前运算符 --------------| 优先级表
};
2.3 算法
switch( priority( optr.top(), *S ) ) {
case '<': //栈顶运算符优先级更低
optr.push( *S ); S++; break; //计算推迟,当前运算符进栈
case '=': //优先级相等(当前运算符为右括号,或尾部哨兵'\0')
optr.pop(); S++; break; //脱括号并接收下一个字符
case '>': {
char op = optr.pop();
if ( '!' == op ) opnd.push( calcu( op, opnd.pop() ) ); //一元运算符
else {
double opnd2 = opnd.pop(), opnd1 = opnd.pop(); //二元运算符
opnd.push( calcu( opnd1, op, opnd2 ) ); //实施计算,结果入栈
}
break;
}
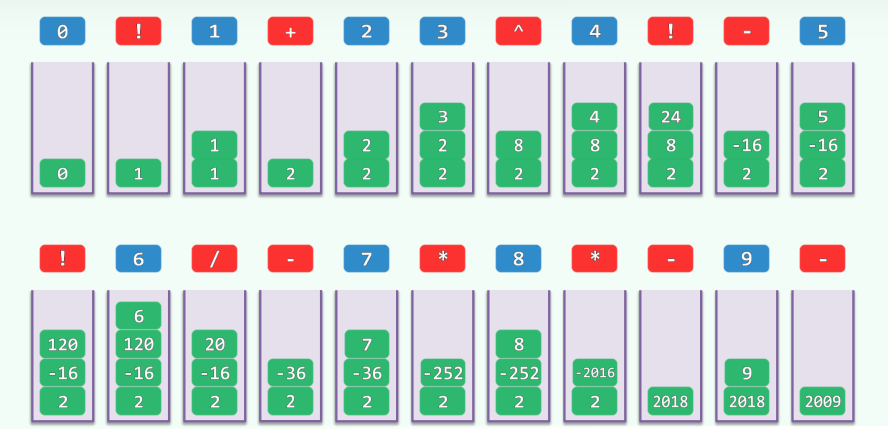
七、逆波兰表达式
1.定义与求值
1.1 逆波兰
-
在由运算符(operator)和操作数(operand)组成的表达式中不使用括号(parenthesis-free),即可表示带优先级的运算关系
-
实例
- 0! +123 +4*(5*6! +7! /8)/9 -> 0! 123 + 4 5 6 ! * 7! 8/ +*9/ +
- (0! +1)^(2*3! +4-5)-6!/(7+8+9) -> 0! 1+23! *4+5-^6! 78+9/-
-
相对于日常使用的中缀式(infix),RPN亦称作后缀式(postfix)
-
作为补偿,须额外引入一个起分隔作用的元字符(比如空格)(较之原表达式,未必更短)
1.2 栈式求值
-
引入栈S (存放操作数),逐个处理下一元素x,
-
if ( x是操作数 ) 将x压入S
-
else(运算符无需缓冲) 从S中弹出x所需数目的操作数;执行相应的计算,结果压入S(无需顾及优先级)
-
返回栈顶
-
-
只要输入的RPN语法正确,此时的栈顶亦是栈底,对应于最终的计算结果
1.3 实例
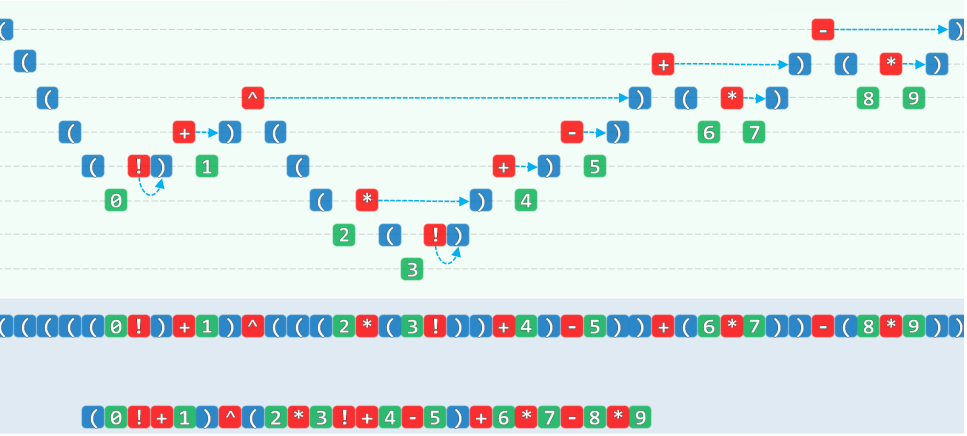
2.转换
2.1 手工转换
- 添加括号
- 以运算符替换右括号,清除左括号
2.2 自动转换
double evaluate( char* S, char* RPN ) { //RPN转换
while ( ! optr.empty() ) { //逐个处理各字符,直至运算符栈空
if ( isdigit( * S ) ) { //若当前字符为操作数,则直接
readNumber( S, opnd );
append( RPN, opnd.top() );
} //将其接入RPN
else //若当前字符为运算符
switch( priority( optr.top(), *S ) ) {
case '>': { //且可立即执行,则在执行相应计算的同时
char op = optr.pop(); append( RPN, op ); //将其接入RPN
}
}
}
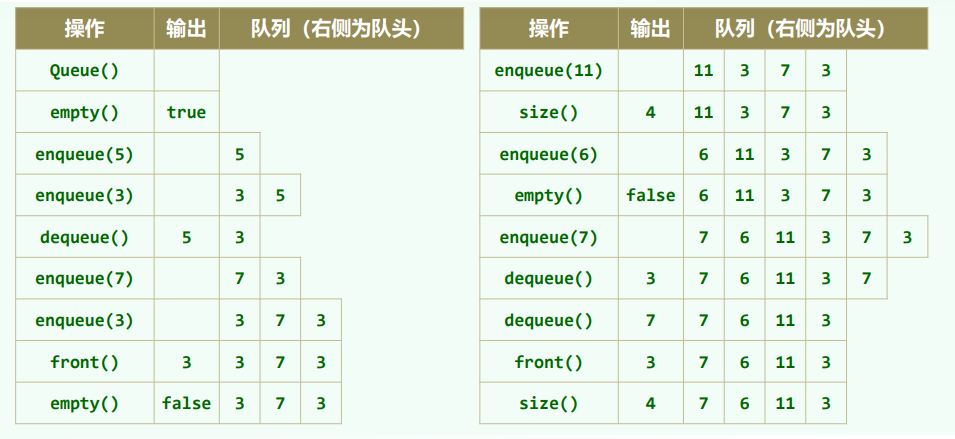
八、队列
1.操作与接口
-
队列(queue)也是受限的序列
-
只能在队尾插入(查询)
- enqueue() / rear()
-
只能在队头删除(查询)
- dequeue() / front()
-
先进先出(FIFO)后进后出(LILO)
2.代码
- 队列既然属于序列的特例,故亦可直接基于向量或列表派生
template<typename T> class Queue: public List {
public: //原有接口一概沿用
void enqueue( T const & e ) { insertAsLast( e ); } //入队
T dequeue() { return remove( first() ); } //出队
T & front() { return first()->data; } //队首
};
- 如此实现的队列接口,均只需O(1)时间

































 3513
3513











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








