文章目录
一、散列
1.循对象访问
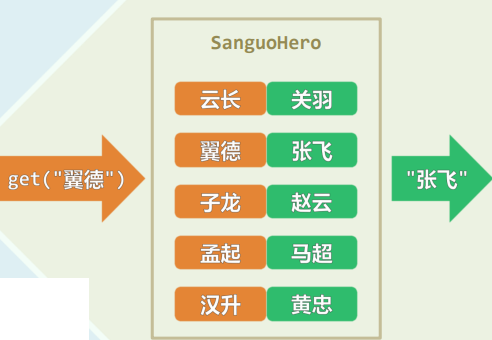
1.1 联合数组:更直接、更有效的访问
- 根据数据元素的取值,直接访问
- style[“关羽”] = “云长”
- style[“张飞”] = “翼德”
- style[“赵云”] = “子龙”
- style[“马超”] = “孟起”
- 下标不再是整数,甚至没有大小次序 ——更为直观、便捷
1.2 词条(entry)~ 映射/词典(Map/Dictionary)
- entry = (key, value)
- Map/Dictionary:词条的集合
- 关键码禁止/允许雷同
- get(key) put(key, value) remove(key)
- 关键码未必可定义大小,元素类型较BST更多样
- 查找对象不限于最大/最小词条,接口功能较PQ更强大
1.3 词典
template <typename K, typename V> //key、value
struct Dictionary {
virtual int size() = 0;
virtual bool put( K, V ) = 0;
virtual V* get( K ) = 0;
virtual bool remove( K ) = 0;
};
- 词典中的词条只需支持判等/比对操作
2.原理
2.1 电话:号码 ~ 人

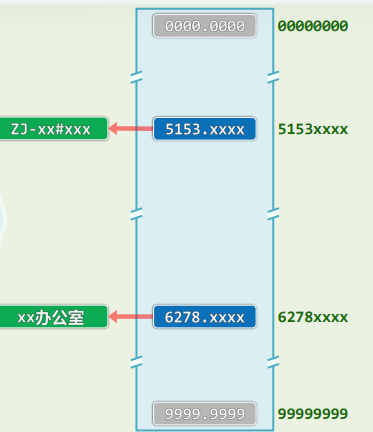
2.2 电话簿
- 需求: 为一所学校制作电话簿
- 号码 --> 教员、学生、员工、办公室
- 蛮力: 用户记录 ~ 数组Rank ~ 电话号码 (O(1)效率)
- 可能的电话 = R= 10^8 = 100M ,实有的电话 = N= 25,000 = 25K
- 问题:
- 空间 = O(R/N)= O(100M + 25K)
- 效率 = 25K / 100M = 0.025%
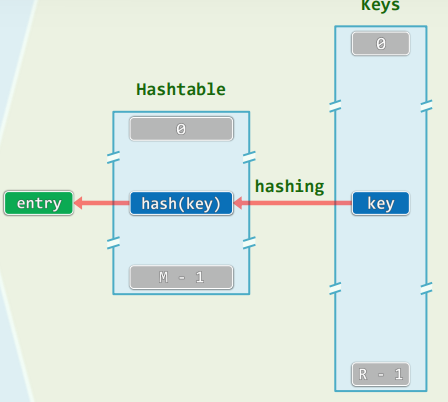
2.3 散列表 / 散列函数
-
桶(bucket):直接存放或间接指向一个词条
-
Bucket array ~ Hashtable(哈希表)
- 容量:M
- 满足: N < M < < R N<M<<R N<M<<R
- 空间:O(N+M)=O(N)
-
定址/杂凑/散列
- 根据词条的key(未必可比较)
- “直接”确定散列表入口(无论表有多长)
-
散列函数: hash():key->&entry
-
“直接”:expected-O(1)≠O(1)
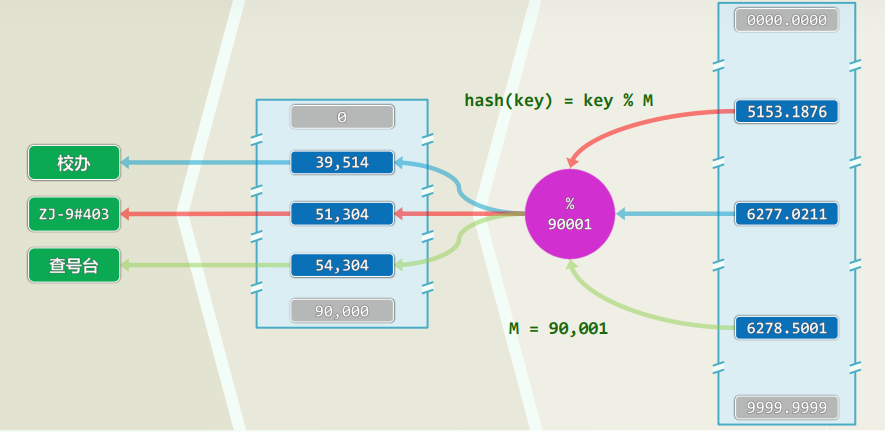
2.4 实例
3.冲突
3.1 同义词(synonym)
k e y 1 ≠ k e y 2 key_1≠key_2 key1=key2 but h a s h ( k e y 1 ) = h a s h ( k e y 2 ) hash(key_1)=hash(key_2) hash(key1)=hash(key2)
3.2 装填因子 vs. 冲突
- load factor:λ=N/M
- λ越大/小
- 空间利用率越高/低
- 冲突的情况越严重/轻微
- 通过降低λ,冲突程度将会有所改善,但只要数据集在动态变化,就无法彻底杜绝
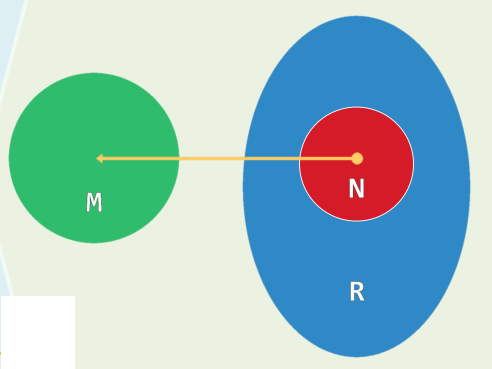
3.3 完美散列
-
在某些条件下,的确可以实现单射(injection)式散列
-
数据集已知且固定时,可实现完美散列(perfect hashing)
-
采用两级散列模式
-
仅需O(n)空间
-
关键码之间互不冲突
-
最坏情况下的查找时间也不过O(1)
-
-
不过在一般情况下,完美散列可期不可求
3.4 生日悖论
- 将在座同学(对应的词条)按生日(月/日)做散列存储
- 散列表长M = 365,装填因子 = 在场人数N / 365
- 冲突(至少有两位同学生日相同)的可能性P365(n)
- P365(1) = 0, P365(2) = 1/365, …, P365(22) = 47.6%, P365(23) = 50.7%, …
- 100人的集会:1 - p365(100) = 0.000,031%
- 自7岁起,不吃不喝、无休无息,每小时参加四次
- 到100岁,才有可能期望遇到一次无冲突的集会
- 因此,在装填因子确定之后,散列策略的选取将至关重要,散列函数的设计也很有讲究
3.5 两项基本任务
- 首先(下一节):精心设计散列表及散列函数,尽可能降低冲突的概率
- 同时(再下节):制定可行的预案,以便在发生冲突时,能够尽快予以排解

二、散列函数
1.基本
1.1 评价标准 + 设计原则
-
确定(determinism):同一关键码总是被映射至同一地址
-
快速(efficiency):expected-O(1)
-
满射(surjection):尽可能充分地利用整个散列空间
-
均匀(uniformity):关键码映射到散列表各位置的概率尽量接近,有效避免聚集(clustering)现象
1.2 除余法
-
$hash(key)=key % M $
-
据说M为素数时,数据对散列表的覆盖最充分,分布最均匀 其实对于理想随机的序列,表长是否素数,无关紧要
-
序列的Kolmogorov复杂度:生成该序列的算法,最短可用多少行代码实现?
- 算术级数: 7 12 17 22 27 32 37 42 47 … //单调性/线性:从7开始,步长为5
- 循环级数: 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 … //周期性:12345不断循环
- 英文:data structures and algorithms … //局部性:频率、关联、词根、…
-
实际应用中的数据序列远非理想随机,上述规律性普遍存在
-
蝉的哲学:经长期自然选择,生命周期“取”作素数
1.3 MAD法
- 除余法的缺陷
- 不动点:无论表长M取值如何,总有:hash(0)≡0
- 相关性:[0,R)的关键码尽管系平均分配至M个桶;但相邻关键码的散列地址也必相邻

- Multiply - Add - Divide
- h a s h ( k e y ) = ( a ∗ k e y + b ) % M , M 为素数, a > 0 , b > 0 ,且 a % M ≠ 0 hash(key) = (a * key + b) \% M,M 为素数,a>0,b>0,且a \% M ≠ 0 hash(key)=(a∗key+b)%M,M为素数,a>0,b>0,且a%M=0
1.4 更多散列函数
-
数字分析(selecting digits) :抽取key中的某几位,构成地址
- 比如,取十进制表示的奇数位
-
平方取中(mid-square) :取 k e y 2 key^2 key2的中间若干位,构成地址
- h a s h ( 123 ) = m i d d l e ( 123 ∗ 123 ) = 1 512 ‾ 9 = 512 hash(123)=middle(123 * 123)=1 \underline{512} 9=512 hash(123)=middle(123∗123)=15129=512
-
折叠法(folding) :将key分割成等宽的若干段,取其总和作为地址
- hash( 123 456 789 ) = 123 + 456 + 789 = 1368 //自左向右
- hash( 123 456 789 ) = 123 + 654 + 789 = 1566 //往复折返
-
位异或法(XOR) :将key分割成等宽的二进制段,经异或运算得到地址
- hash( 110 011 011 b ) = 110 ^ 011 ^ 011 = 110b //自左向右
- hash( 110 011 011 b ) = 110 ^ 110 ^ 011 = 011b //往复折返
-
总之,越是随机,越是没有规律,越好
2.随机数
2.1 (伪)随机数法
-
循环: rand( x + 1 ) = [ a * rand( x ) ] % M //M素数,a % M ≠ 0
- a = 7 5 = 16 , 807 = 10000011010011 1 b a = 7^5 = 16,807 = 100000110100111_b a=75=16,807=100000110100111b
- M = 2 31 – 1 = 2 , 147 , 483 , 647 = 0111111111111111111111111111111 1 b M = 2^{31} – 1 = 2,147,483,647 = 01111111 11111111 11111111 11111111_b M=231–1=2,147,483,647=01111111111111111111111111111111b
-
径取:hash(key) = rand(key) = [ r a n d ( 0 ) ∗ a k e y rand(0) * a^{key} rand(0)∗akey] % M
-
种子:rand(0) = ?
-
把难题推给伪随机数发生器,但是(伪)随机数发生器的实现,因具体平台、不同历史版本而异,创建的散列表可移植性差——故需慎用此法
unsigned long int next = 1; //sizeof(long int) = 8
void srand(unsigned int seed) { next = seed; } //sizeof(int) = 4 or 8
int rand(void) { //1103515245 = 3^5 * 5 * 7 * 129749
next = next * 1103515245 + 12345;
return (unsigned int)(next/65536) % 32768;
}
int rand() { int uninitialized; return uninitialized; }
char* rand( t_size n ) { return ( char* ) malloc( n ); }

2.2 就地随机置乱:任给一个数组A[0, n),理想地将其中元素的次序随机打乱
void shuffle( int A[], int n ) {
for ( ; 1 < n; --n ) //自后向前,依次将各元素
swap( A[ rand() % n ], A[ n - 1 ] ); //与随机选取的某一前驱(含自身)交换
} //20! < 2^64 < 21!

3.hashCode与多项式法
3.1 任意类型->整数型
- h a s h C o d e ( “ x n − 1 . . . x 2 x 1 x 0 " ) = x n − 1 ⋅ a n − 1 + . . . + x 2 ⋅ a 2 + x 1 ⋅ a 1 + x 0 = ( . . . ( ( x n − 1 ⋅ a + x n − 2 ) ⋅ a ) + . . . + x 1 ) ⋅ a + x 0 \begin{aligned} hashCode(“x_{n-1}...x_2x_1x_0")&=x_{n-1}·a^{n-1}+...+x_2·a^2+x_1·a^1+x_0 \\ &=(...((x_{n-1}·a+x_n-2)·a)+...+x_1)·a+x_0 \\ \end{aligned} hashCode(“xn−1...x2x1x0")=xn−1⋅an−1+...+x2⋅a2+x1⋅a1+x0=(...((xn−1⋅a+xn−2)⋅a)+...+x1)⋅a+x0
3.2 冲突 ~ 巧合
-
h a s h C o d e ( S ) = ∑ c ∈ S c o d e ( u p p e r ( c ) ) hashCode(S)=\sum_{c∈S}code(upper(c)) hashCode(S)=∑c∈Scode(upper(c))
- h a s h C o d e ( “ h a s h ” ) = 8 + 1 + 19 + 8 = 36 hashCode(“hash”)=8+1+19+8=36 hashCode(“hash”)=8+1+19+8=36
-
字符相对次序信息丢失,将引发大量冲突
- I am Lord Voldemort
- Tom Marvolo Riddle
-
即便字符不同、数目不等
- He’s Harry Potter
三、排解冲突
1.开放散列
1.1 多槽位(Multiple Slots)
-
Multiple Slots
- 桶单元细分成若干槽位
- 存放(与同一单元)冲突的词条
-
只要槽位数目不太多 依然可以保证O(1)的时间效率
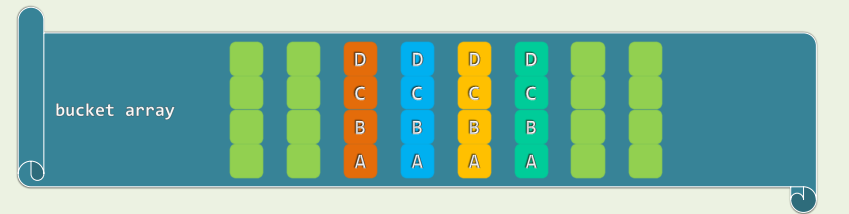
- 需要细分到什么程度
- 过细,空间浪费;反过来
- 无论多细,极端情况下仍可能不够
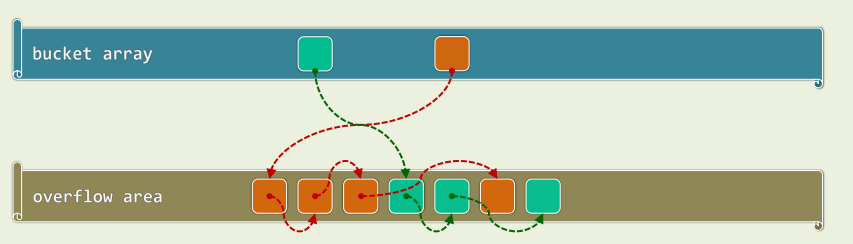
1.2 公共溢出区(Overflow Area)
- 单独开辟一块连续空间 发生冲突的词条,顺序存入此区域
- 结构简单,算法易于实现
- 但是,不冲突则已,一旦发生冲突,最坏情况下,处理冲突词条所需的时间将 正比于溢出区的规模
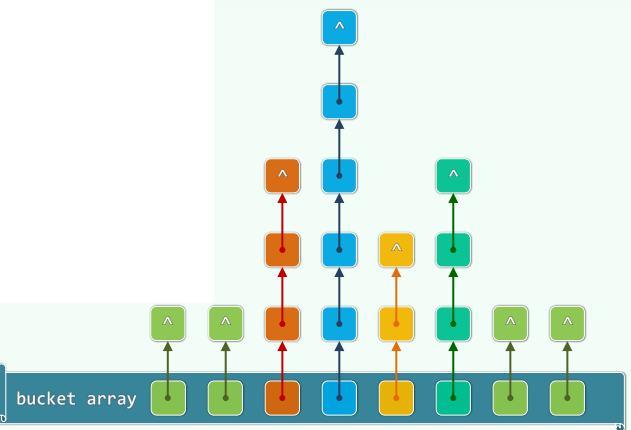
1.3 独立链 (Linked-List Chaining / Separate Chaining)
- 每个桶拥有一个列表,存放对应的一组同义词
- 优点
- 无需为每个桶预备多个槽位
- 任意多次的冲突都可解决
- 删除操作实现简单、统一
- 但是,指针本身占用空间,节点的动态分配和回收需耗时间 更重要的是空间未必连续分布,系统缓存很难生效
2.封闭散列
2.1 开放定址
-
闭散列方法(Closed Hashing),必然对应于开放定址(Open Addressing)
- 只要有必要,任何散列桶都可以接纳任何词条
-
检测序列(Probe Sequence/Chain):为每个词条,都需事先约定若干备用桶,优先级逐次下降
-
查找算法:沿试探链,逐个转向下一桶单元,直到命中成功,或者抵达一个空桶而失败
2.2 线性试探
-
Linear Probing
- 一旦冲突,则试探后一紧邻的桶
- 直到命中(成功),或抵达空桶(失败)
-
[ hash( key ) + 1 ] % M->[ hash( key ) + 2 ] % M->[ hash( key ) + 3 ] % M->[ hash( key ) + 4 ] % M

-
在散列表内部解决冲突,无需附加的指针、链表或溢出区等,整体结构保持简洁
-
只要还有空桶,迟早会找到
-
新增非同义词之间的冲突
-
数据堆积(clustering)现象严重
-
好在,试探链连续,数据局部性良好
-
通过装填因子,冲突与堆积都可有效控制
2.3 插入+删除

- 插入:新词条若尚不存在,则存入试探终止处的空桶
- 试探链:可能因而彼此串接、重叠!
- 删除:经过它的试探链都将因此断裂,导致后续词条丢失——明明存在,却访问不到
3.懒惰删除
3.1 Lazy Removal:故居 ~ 空宅
Bitmap* removed用Bitmap懒惰地标记被删除的桶int L被标记桶的数目
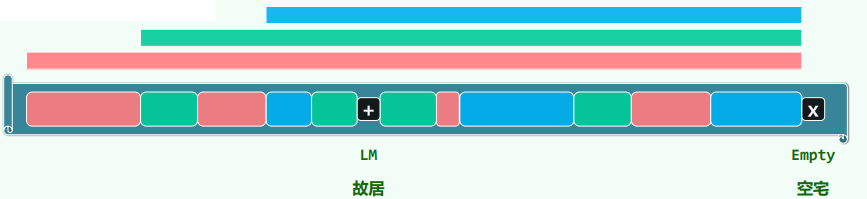
- 仅做标记,不对试探链做更多调整——此后,带标记的桶,角色因具体的操作而异
- 查找词条时,被视作“必不匹配的非空桶”,试探链在此得以延续
- 插入词条时,被视作“必然匹配的空闲桶”,可以用来存放新词条
3.2 两种算法
template<typename K,typename V> int Hashtable::probe4Hit(const K& k) {
int r = hashCode(k) % M; //按除余法确定试探链起点
while ( ( ht[r] && (k != ht[r]->key) ) || removed->test(r) )
r = ( r + 1 ) % M; //线性试探(跳过带懒惰删除标记的桶)
return r; //调用者根据ht[r]是否为空及其内容,即可判断查找是否成功
}
template<typename K,typename V> int Hashtable::probe4Free(const K& k) {
int r = hashCode(k) % M; //按除余法确定试探链起点
while ( ht[r] ) r = (r + 1) % M; //线性试探,直到空桶(无论是否带有懒惰删除标记)
return r; //只要有空桶,线性试探迟早能找到
}
4.重散列(Rehashing)
template<typename K,typename V> //随着装填因子增大,冲突概率、排解难度都将激增
void Hashtable::rehash() { //此时,不如“集体搬迁”至一个更大的散列表
int oldM = M; Entry** oldHt = ht;
ht = new Entry*[ M = primeNLT( 4 * N ) ]; N = 0; //新表“扩”容
memset( ht, 0, sizeof( Entry* ) * M ); //初始化各桶
release( removed ); removed = new Bitmap(M); L = 0; //懒惰删除标记
for ( int i = 0; i < oldM; i++ ) //扫描原表
if ( oldHt[i] ) //将每个非空桶中的词条
put( oldHt[i]->key, oldHt[i]->value ); //转入新表
release( oldHt ); //释放——因所有词条均已转移,故只需释放桶数组本身
}
template<typename K,typename V> bool Hashtable::put( K k, V v ) {
if ( ht[ probe4Hit( k ) ] ) return false; //雷同元素不必重复插入
int r = probe4Free( k ); //为新词条找个空桶(只要装填因子控制得当,必然成功)
ht[ r ] = new Entry( k, v ); ++N; //插入
if ( removed->test( r ) ) { removed->clear( r ); --L; } //懒惰删除标记
if ( (N + L)*2 > M ) rehash(); //若装填因子高于50%,重散列
return true; 插入
}
template<typename K,typename V> bool Hashtable::remove( K k ) {
int r = probe4Hit( k ); if ( !ht[r] ) return false; //确认目标词条确实存在
release( ht[r] ); ht[r] = NULL; --N; //清除目标词条
removed->set(r); ++L; //更新标记、计数器
if ( 3*N < L ) rehash(); //若懒惰删除标记过多,重散列
return true;
}
5.平方试探
5.1 平方试探(Quadratic Probing)
-
Quadratic Probing:以平方数为距离,确定下一试探桶单元
- [ h a s h ( k e y ) + 1 2 ] % M [ hash(key) + 1^2 ] \% M [hash(key)+12]%M
- [ h a s h ( k e y ) + 2 2 ] % M [ hash(key) + 2^2 ] \% M [hash(key)+22]%M
-
数据聚集现象有所缓解
- 试探链上,各桶间距线性递增
- 一旦冲突,可“聪明”地跳离是非之地
-
对于大散列表,I/O操作有所增加

5.2 素数表长时,只要λ<0.5就一定能够找出;否则,不见得
-
{
0
,
1
,
2
,
3
,
4
,
5
,
.
.
.
}
2
%
12
=
{
0
,
1
,
4
,
9
}
\{ 0, 1, 2, 3, 4, 5, ... \}^2 \% 12 = \{ 0, 1, 4, 9 \}
{0,1,2,3,4,5,...}2%12={0,1,4,9}
- M若为合数: n 2 % M n^2\%M n2%M可能的取值可能少于 ⌈ M / 2 ⌉ \lceil M/2 \rceil ⌈M/2⌉种——此时,只要对应的桶均非空
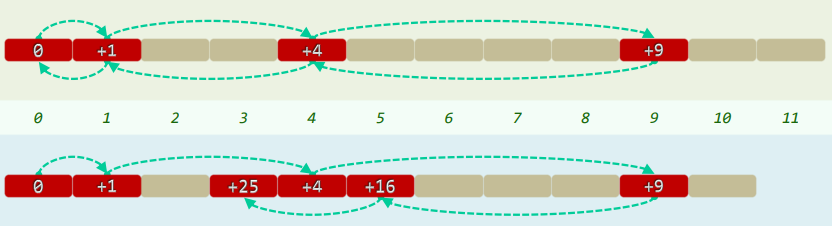
-
{
0
,
1
,
2
,
3
,
4
,
5
,
.
.
.
}
2
%
11
=
{
0
,
1
,
4
,
9
,
5
,
3
}
\{ 0, 1, 2, 3, 4, 5, ... \}^2 \% 11 = \{ 0, 1, 4, 9,5,3 \}
{0,1,2,3,4,5,...}2%11={0,1,4,9,5,3}
- 若M为素数, n 2 % M n^2\%M n2%M恰有 ⌈ M / 2 ⌉ \lceil M/2 \rceil ⌈M/2⌉种取值,且由试探链的前 ⌈ M / 2 ⌉ \lceil M/2 \rceil ⌈M/2⌉项取遍
5.3 每一条试探链,都有足够长的无重前缀
- 反证:假设存在 0 ≤ a ≤ b < ⌈ M / 2 ⌉ 0≤a≤b<\lceil M/2 \rceil 0≤a≤b<⌈M/2⌉,使得沿着试探链,第a项和第b项彼此冲突
- 于是:
a
2
a^2
a2和%b^2%自然关于M同余,亦即
- a 2 ≡ b 2 ( m o d M ) a^2\equiv b^2(mod M) a2≡b2(modM)
- b 2 − a 2 = ( b + a ) ( b − a ) ≡ 0 ( m o d M ) b^2-a^2=(b+a)(b-a)\equiv 0(mod M) b2−a2=(b+a)(b−a)≡0(modM)
- 然而,
0
<
b
−
a
≤
b
+
a
<
⌈
M
/
2
⌉
+
(
⌈
M
/
2
⌉
+
1
)
≤
⌈
M
/
2
⌉
+
⌈
M
/
2
⌉
=
M
0<b-a≤b+a<\lceil M/2 \rceil+(\lceil M/2 \rceil+1)≤\lceil M/2 \rceil+\lceil M/2 \rceil=M
0<b−a≤b+a<⌈M/2⌉+(⌈M/2⌉+1)≤⌈M/2⌉+⌈M/2⌉=M
- 无论b-a还是b+a都不可能整除M
6.双向平方试探
6.1 策略:交替地沿两个方向试探,均按平方确定距离
- [ h a s h ( k e y ) + 1 2 ] % M [ hash(key) + 1^2 ] \% M [hash(key)+12]%M, [ h a s h ( k e y ) + 2 2 ] % M [ hash(key) + 2^2 ] \% M [hash(key)+22]%M
- [ h a s h ( k e y ) − 1 2 ] % M [ hash(key) - 1^2 ] \% M [hash(key)−12]%M, [ h a s h ( k e y ) − 2 2 ] % M [ hash(key) - 2^2 ] \% M [hash(key)−22]%M
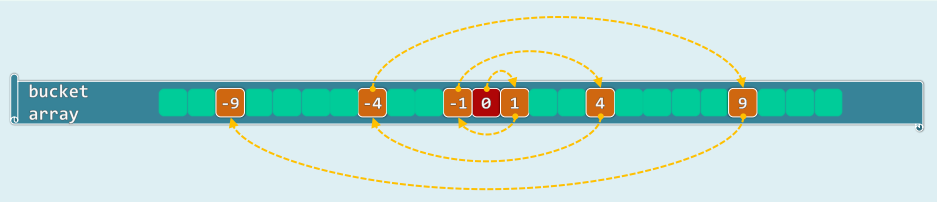
6.2 子试探链
- 正向和反向的子试探链,各自包含
⌈
M
/
2
⌉
\lceil M/2 \rceil
⌈M/2⌉个互异的桶
- ⌊ M / 2 ⌋ , . . . , − 3 , − 2 , − 1 ‾ , 0 , 1 , 2 , 3 , . . . , ⌊ M / 2 ⌋ ‾ \underline{\lfloor M/2 \rfloor,...,-3,-2,-1},0,\underline{1,2,3,...,\lfloor M/2 \rfloor} ⌊M/2⌋,...,−3,−2,−1,0,1,2,3,...,⌊M/2⌋
6.3 4k+3
- 表长取作素数M=4k+3,即必然可以保证试探链的前M项均互异
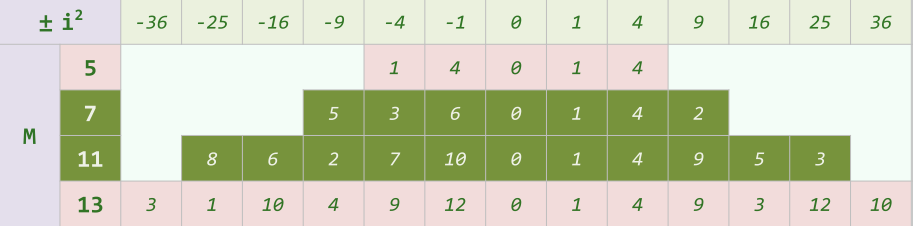
6.4 费马二平方定理(Two-Square Theorem of Fermat)
-
任一素数p可表示为一对整数的平方和,当且仅当 p ≡ 1 ( m o d M ) p\equiv 1(mod M) p≡1(modM)
-
只要注意到: ( u 2 + v 2 ) ( s 2 + t 2 ) = ( u s + v t ) 2 + ( u t − v s ) 2 = ( u s − v t ) 2 + ( u t + v s ) 2 (u^2+v^2)(s^2+t^2)=(us+vt)^2+(ut-vs)^2=(us-vt)^2+(ut+vs)^2 (u2+v2)(s2+t2)=(us+vt)2+(ut−vs)2=(us−vt)2+(ut+vs)2
-
就不难推知:自然数n可表示为一对整数的平方和,当(且仅当)它的每一 M=4k+3类的素因子均为偶数次方
7.双散列(Double Hashing)
-
预先约定第二散列函数: h a s h 2 ( k e y , i ) hash_2(key,i) hash2(key,i)
-
冲突时,由其确定偏移增量,确定下一试探位置: [ h a s h ( k e y ) + ∑ i = 1 k h a s h 2 ( k e y , i ) ] % M [hash(key)+\sum_{i=1}^{k}hash_2(key,i)]\%M [hash(key)+∑i=1khash2(key,i)]%M
-
线性试探: h a s h 2 ( k e y , i ) ≡ 1 hash_2(key,i) \equiv 1 hash2(key,i)≡1
-
平方试探: h a s h 2 ( k e y , i ) = 2 i − 1 hash_2(key,i)=2i-1 hash2(key,i)=2i−1
-
更一般地,偏移增量同时还与key相关

四、桶排序
1.算法
1.1 简单情况
- 对[0,m)内的n(<m)个互异整数 借助散列表H[]做排序
- 空间 = O(m),时间 = O(n)
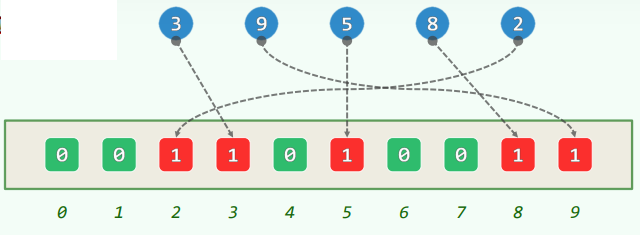
1.2 一般情况
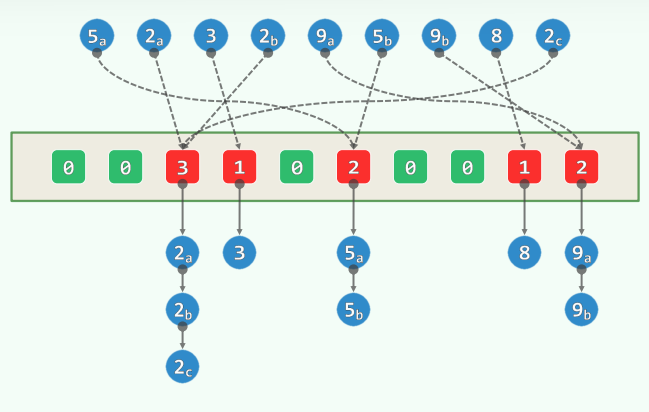
- 若允许重复 (可能m << n)
- 依然使用散列表
- 每一组同义词各成一个链表
- 空间 = O(m + n),时间 = O(n)
2.最大缝隙
2.1 最大缝隙(MaxGap)

- 任意n个互异点均将实轴分为n-1段有界区间,其中的哪一段最长
- 如果不追求效率,显而易见的方法莫过于
- 对所有点排序 //Ω(nlogn)
- 依次计算各相邻点对的间距,保留最大者 //Θ(n)
- 采用分桶策略,可改进至O(n)时间
2.2 线性算符

-
找到最左点、最右点 O(n) //一趟线性扫描
-
将有效范围均匀地划分为n-1段(n个桶) O(n) //相当于散列表
-
通过散列,将各点归入对应的桶 O(n) //模余法
-
在各桶中,动态记录最左点、最右点 O(n) //可能相同甚至没有
-
算出相邻(非空)桶之间的“距离” O(n) //一趟遍历足矣
-
最大的距离即MaxGap O(n) //画家算法
2.3 正确性
- MaxGap至少跨越两个桶,等价地,MaxGap不可能局限于某一个桶内
五、基数排序
1.算法与实现
1.1 词典序
- 有时,关键码由多个域组成: k d , k t − 1 , . . . , k 1 k_d , k_{t-1} , ... , k_1 kd,kt−1,...,k1
- 若将各域视作字母,则关键码即单词——按词典的方式排序(lexicographic order)
1.2 算法:自 k 1 k_1 k1到 k t k_t kt(低位优先),依次以各域为序做一趟桶排序
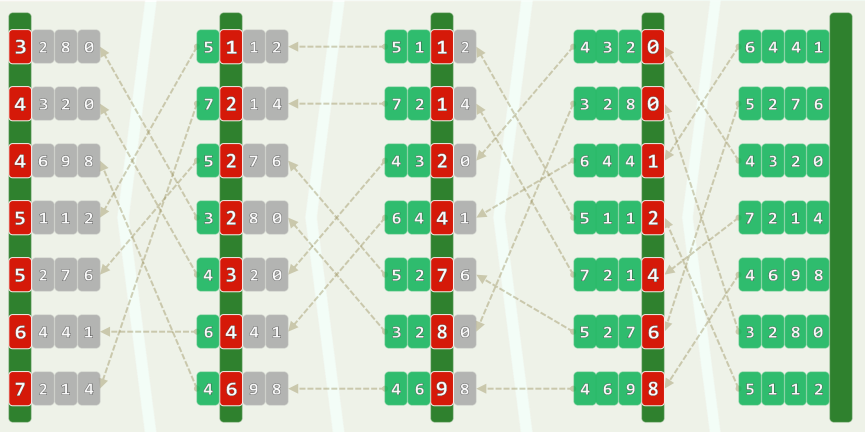
1.3 正确性
- 归纳假设:前i趟排序后,所有词条关于低i位有序 (第1趟显然)
- 假设前i-1趟均成立,现考查第i趟排序之后的时刻
- 无非两种情况
- 凡第i位不同的词条,即便此前曾是逆序,现在亦必已转为有序
- 凡第i位相同的词条,得益于桶排序的稳定性,必保持原有次序
1.4 时间成本
时间成本 = 各趟桶排序所需时间之和 = n + 2 m 1 + n + 2 m 2 + . . . + n + 2 m d / / m 为各域 k 的取值范围 = O ( d ∗ ( n + m ) ) / / m = m a x { m 1 , . . . , m d } \begin{aligned} 时间成本&=各趟桶排序所需时间之和 \\ &=n + 2m_1 + n + 2m_2 + ... + n + 2m_d //m 为各域 k 的取值范围\\ &=O( d * (n + m) ) //m = max\{ m_1, ..., m_d \}\\ \end{aligned} 时间成本=各趟桶排序所需时间之和=n+2m1+n+2m2+...+n+2md//m为各域k的取值范围=O(d∗(n+m))//m=max{m1,...,md}
- 当m = O(n)且d可视作常数时,O(n)
- 在一些特定场合,Radixsort非常高效
1.5 实现(以二进制无符号整数为例)
typedef unsigned int U; //约定:类型T或就是U;或可转换为U,并依此定序
template<typename T> void List<T>::radixSort( ListNodePosi p, int n ) {
ListNodePosi<T> head = p->pred; ListNodePosi<T> tail = p;
for ( int i = 0; i < n; i++ ) tail = tail->succ; //待排序区间为(head, tail)
for ( U radixBit = 0x1; radixBit && (p = head); radixBit <<= 1 ) //以下反复地
for ( int i = 0; i < n; i++ ) //根据当前基数位,将所有节点
radixBit & U (p->succ->data) ? //分拣为前缀(0)与后缀(1)
insert( remove( p->succ ), tail ) : p = p->succ;
} //为避免remove()、insert()的低效率,可拓展List::move(p,tail)接口,将节点p直接移至tail之前
1.6 实例
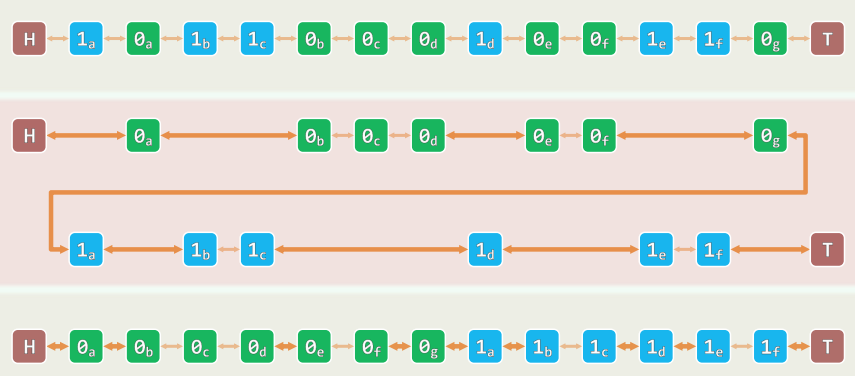
2.整数排序
2.1 常对数密度的整数集
-
设d>1为常数
-
考查取自 [ 0 , n d ) [0,n^d) [0,nd)内的n个整数
- 常规密度 = n / n d = 1 / n d − 1 → 0 =n/n^d=1/n^{d-1}\rightarrow0 =n/nd=1/nd−1→0
- 对数密度 = ln n / ln n d = 1 / d = O ( 1 ) =\ln n/\ln n^d=1/d=O(1) =lnn/lnnd=1/d=O(1)
-
亦即,这类整数集的对数密度不超过常数
-
若取d=4,则即便是64位整数,也只需 n > ( 2 64 ) 1 / 4 = 2 16 = 65 , 356 n>(2^{64})^{1/4}=2^{16}=65,356 n>(264)1/4=216=65,356
2.2 线性排序算法
- 预处理:将所有元素转换为n进制形式: x = ( x d , . . . , x 3 , x 2 , x 1 ) x=(x_d,...,x_3,x_2,x_1) x=(xd,...,x3,x2,x1)

- 于是,每个元素均转化为d个域,故可直接套用Radixsort算法
- 排序时间=d·(n+n)=P(n)
- 原因在于:
- 整数取值范围有限制
- 不再是基于比较的计算模式
六、计数排序
1.算法
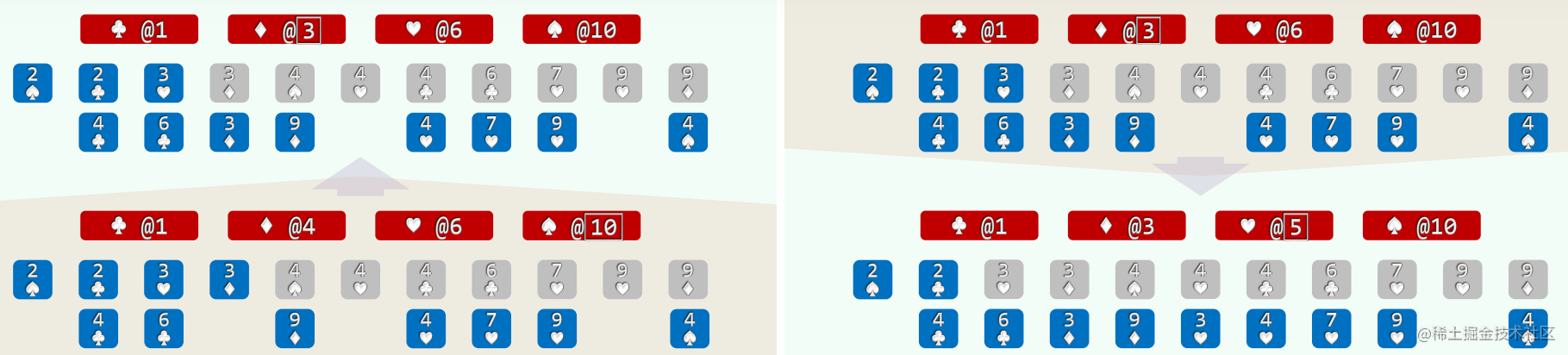
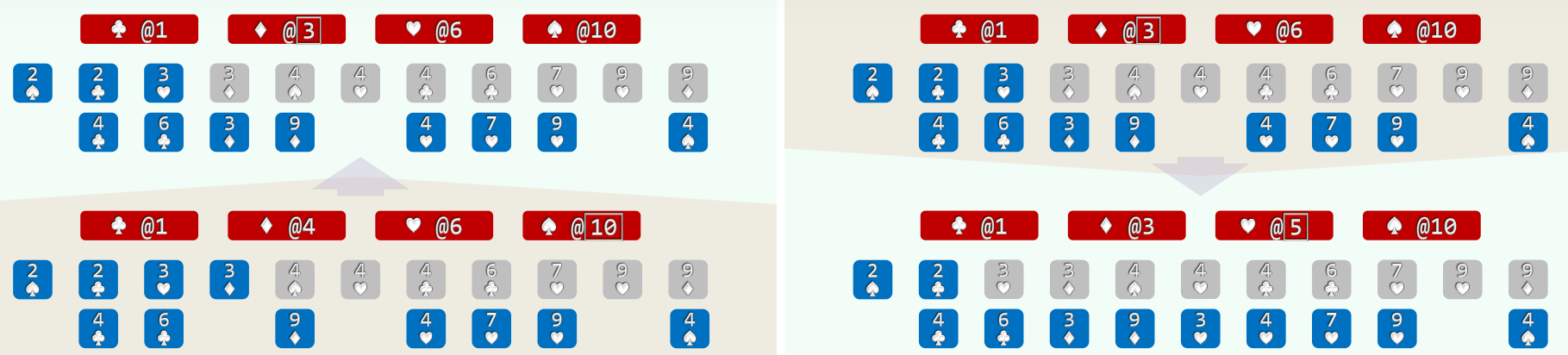
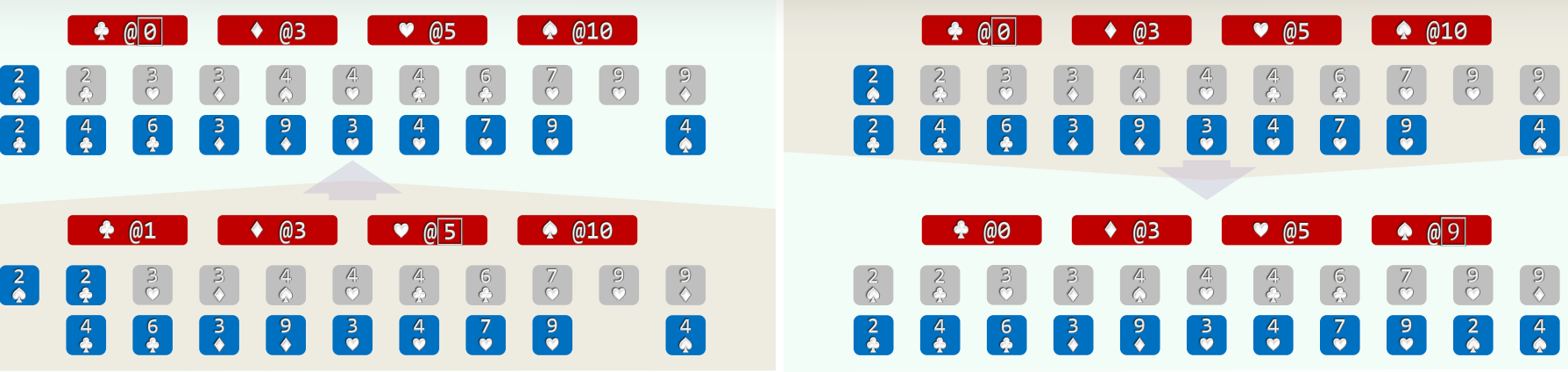
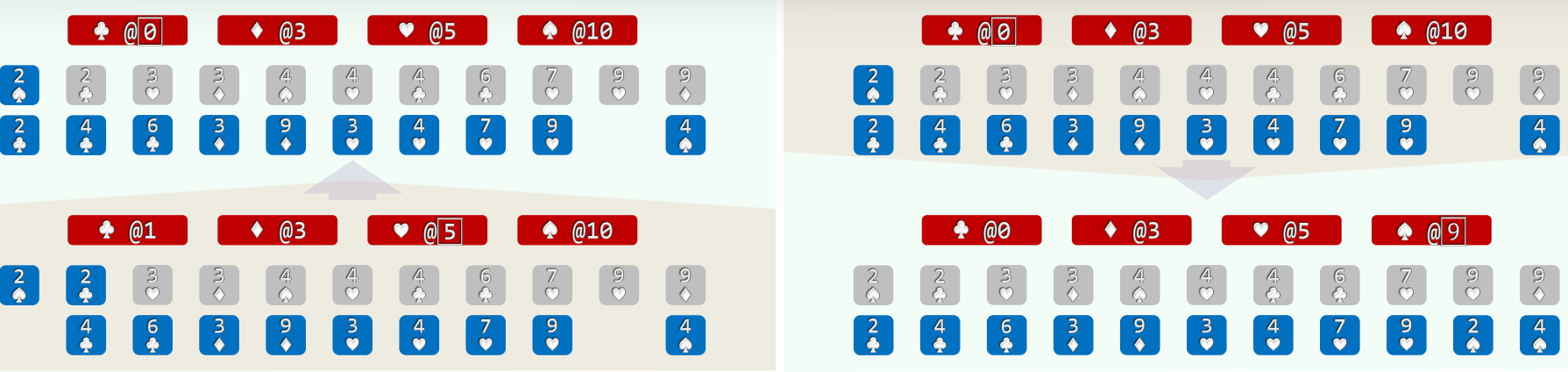
- 以纸牌排序为例(n>>m=4),假设已按点数排序,以下对花色排序

- (1)经过分桶,统计出各种花色的数量 //O(n)
- (2)自前向后扫描各桶,依次累加 (cumulative sum, O(m)), 即可确定各套花色所处的秩区间:[0, 3) + [3, 5) + [5, 9) + [9, 11)
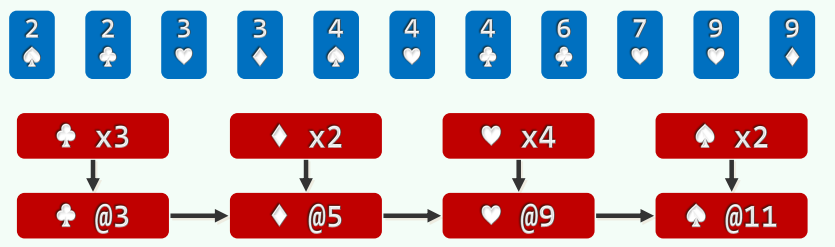
- (3)自后向前扫描每一张牌 (O(n)), 对应桶的计数减一,即是其在最终有序序列中对应的秩
2.实例
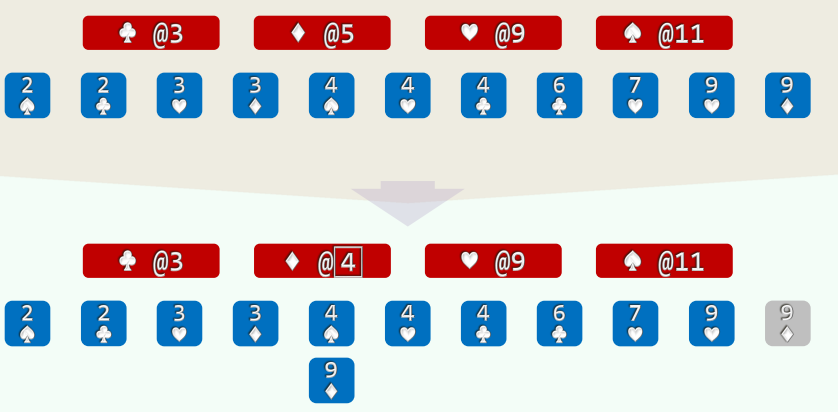
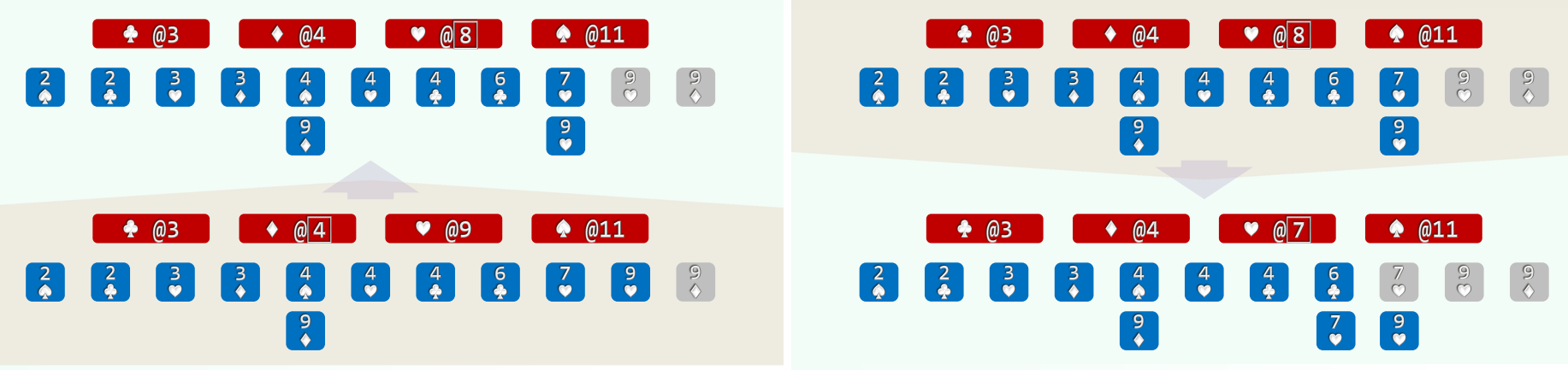
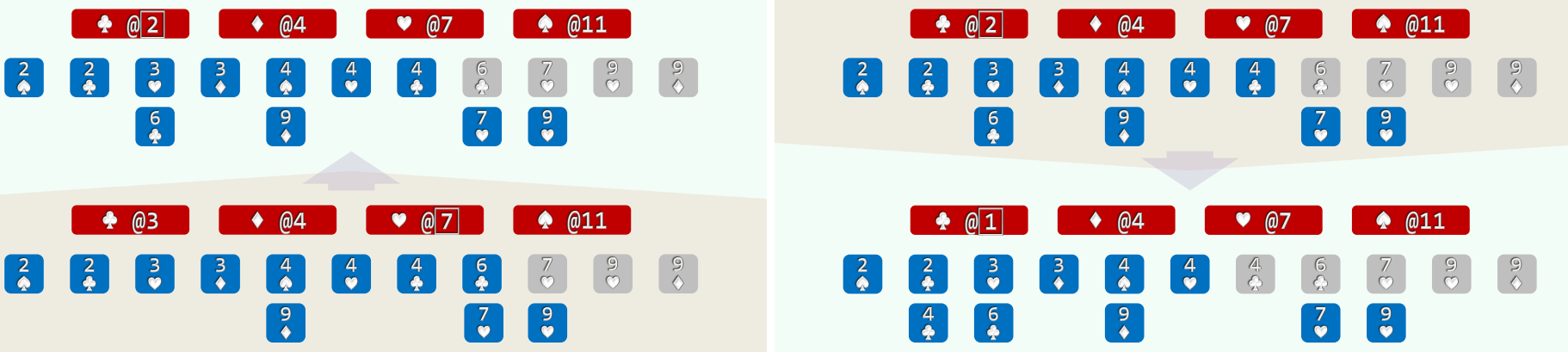





















 457
457











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








