数据结构（c++）学习笔记--高级搜索树

---

一、伸展树

1.逐层伸展

1.1 局部性/Locality：刚被访问过的数据，极有可能很快地再次被访问

1.2 BST的局部性

• 时间：刚被访问过的节点，极有可能很快地再次被访问

• 空间：下一将要访问的节点，极有可能就在刚被访问过节点的附近

• 对AVL连续的m次查找（m >> n），共需$O(m\cdot \log n)$时间

• 自适应链表：节点一旦被访问，随即移动到最前端

• 模仿：BST的节点一旦被访问，随即调整到树根

1.3 逐层伸展

• 节点v一旦被访问 随即被推送至根

• 与其说“推”，不如说“爬” 一步一步地往上爬

• 自下而上，逐层旋转

  • zig( v−>parent )
  • zag( v−>parent )

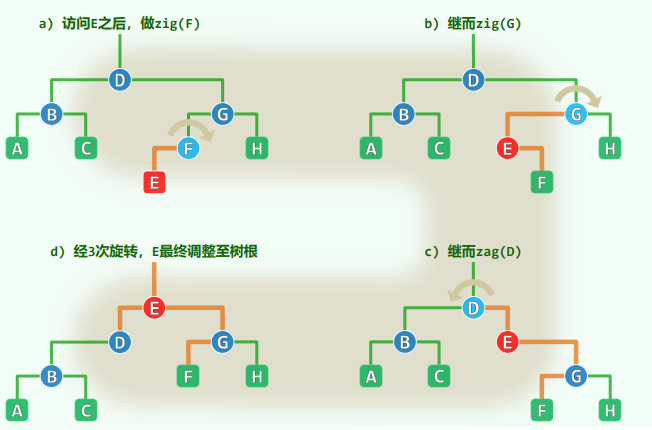
1.4 实例

• 伸展过程的效率这取决于
  • 树的初始形态和
  • 节点的访问次序

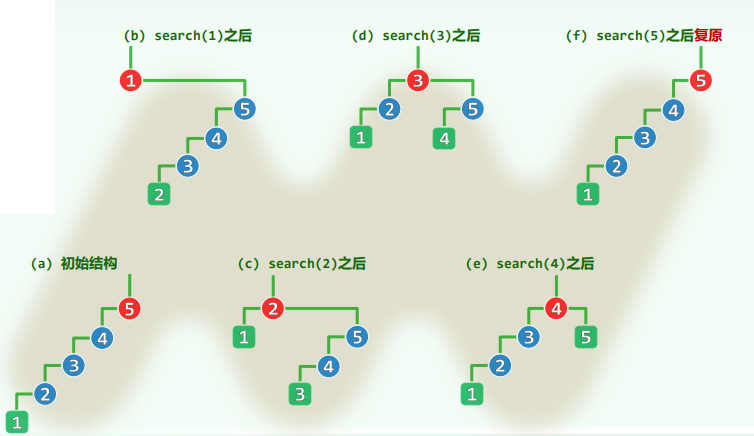
1.5 最坏情况

• 旋转次数呈周期性的算术级数
• 每一周期累计$\Omega (n^2)$分，分摊$\Omega (n)$

2.双层伸展

2.1 双层伸展

• 构思的精髓：向上追溯两层，而非一层
• 反复考察祖孙三代： g = parent§, p = parent(v), v
• 根据它们的相对位置，经两次旋转，使v上升两层，成为（子）树根

2.2 zig-zag / zag-zig

• 时的v按中序遍历次序居中

• 节点访问之后，对应路径的长度随即折半
• 最坏情况不致持续发生，伸展操作分摊仅需$要是v只有父亲，没有祖父呢？此时必有v.parent()==T.root()O(\log n)$时间

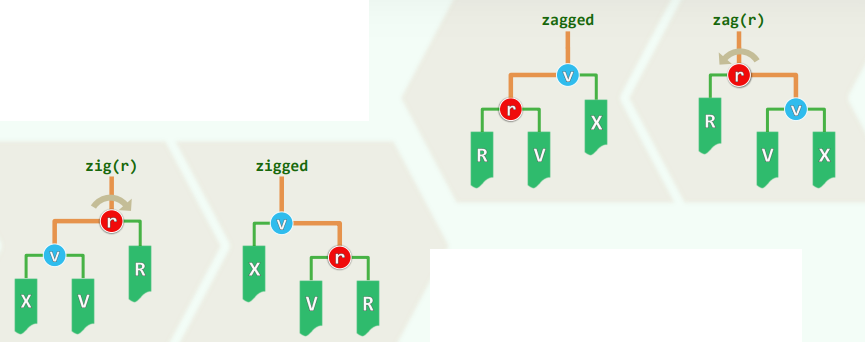
2.3 zig / zag

• 当v只有父亲，没有祖父,此时必有v.parent() == T.root()
• 只需做单次旋转：zig®或zag®

3.算法实现

3.1 接口

template<typename T> class Splay : public BST<T>{
protected: 
    BinNodePosi splay( BinNodePosi v ); //将v伸展至根 
public: //伸展树的查找也会引起整树的结构调整，故search()也需重写 
    BinNodePosi<T> & search( const T & e ); //查找（重写） 
    BinNodePosi<T> insert( const T & e ); //插入（重写） 
    bool remove( const T & e ); //删除（重写） 
};

3.2 伸展算法

template<typename T> BinNodePosic<T> Splay<T>::splay( BinNodePosi<T> v ) { 
    if ( ! v ) return NULL; 
    BinNodePosi<T> p; BinNodePosi<T> g; 
    while ( (p = v->parent) && (g = p->parent) ) {//自下而上，反复双层伸展 
        BinNodePosi<T> gg = g->parent; //每轮之后，v都将以原曾祖父为父 
        if ( IsLChild( * v ) ) 
            if ( IsLChild( * p ) ) { /* zig-zig */ 
                attachAsLC( p->rc, g ); //Y 
                attachAsLC( v->rc, p ); //X 
                attachAsRC( p, g ); 
                attachAsRC( v, p )
            } 
            else { /* zig-zag */ } 
        else 
            if ( IsRChild( * p ) ) { /* zag-zag */ } 
            else { /* zag-zig */ } 
        if ( !gg ) v->parent = NULL; //无曾祖父gg的v即为树根；否则，gg此后应以v为 
        else ( g == gg->lc ) ? attachAsLC(v, gg) : attachAsRC(gg, v); //左或右孩子 
        updateHeight( g ); updateHeight( p ); updateHeight( v );
    } 
    if ( p = v->parent ) { /* 若p果真是根，只需再额外单旋一次 */ } 
    v->parent = NULL; return v; //伸展完成，v抵达树根
}

3.2 查找算法

template<typename T> BinNodePosi<T> & Splay<T>::search( const T & e ) { 
    // 调用标准BST的内部接口定位目标节点 
    BinNodePosi<T> p = BST::search( e ); 
    // 无论成功与否，最后被访问的节点都将伸展至根 
    _root = splay( p ? p : _hot ); //成功、失败 
    // 总是返回根节点 
    return _root;
}

• 伸展树的查找，与常规BST::search()不同,很可能会改变树的拓扑结构，不再属于静态操作

3.3 插入算法

• 直观方法：先调用标准的BST::search()，再将新节点伸展至根
• Splay::search()已集成splay()，查找失败之后，_hot即是根
• 既如此，何不随即就在树根附近接入新节点

template<typename T> BinNodePosi<T> Splay<T>::insert( const T & e ) { 
    if ( !_root ) { _size = 1; return _root = new BinNode<T>( e ); } //原树为空 
    BinNodePosi<T> t = search( e ); 
    if ( e == t->data ) return t; //t若存在，伸展至根 
    if ( t->data < e ) { //在右侧嫁接（rc或为空，lc == t必非空） 
        t->parent = _root = new BinNode<T>( e, NULL, t, t->rc ); 
        if ( t->rc ) { t->rc->parent = _root; t->rc = NULL; } 
    } 
    else { //e < t->data，在左侧嫁接（lc或为空，rc == t必非空） 
        t->parent = _root = new BinNode<T>( e, NULL, t->lc, t ); 
        if ( t->lc ) { t->lc->parent = _root; t->lc = NULL; } 
    }
    _size++; updateHeightAbove( t ); return _root; //更新规模及t与_root的高度，插入成功 
} //无论如何，返回时总有_root->data == e

3.4 删除算法

• 直观方法：调用BST标准的删除算法，再将_hot伸展至根
• 注意到，Splay::search()成功之后，目标节点即是树根
• 既如此，何不随即就在树根附近完成目标节点的摘除

template<typename T> bool Splay<T>::remove( const T & e ) { 
    if ( !_root || ( e != search( e )->data ) ) return false; //若目标存在，则伸展至根 
    BinNodePosi L = _root->lc, R = _root->rc; release(t); //记下左、右子树后，释放之 
    if ( !R ) { //若R空 
        if ( L ) L->parent = NULL; _root = L; //则L即是余树 
    } 
    else { //否则 
        _root = R; R->parent = NULL; search( e ); //在R中再找e：注定失败，但最小节点必 if (L) 
        L->parent = _root; _root->lc = L; //伸展至根，故可令其以L作为左子树 
    }
    _size--; if ( _root ) updateHeight( _root ); //更新记录 
    return true;
}

3.5 综合评价

• 无需记录高度或平衡因子；编程实现简单——优于AVL树，分摊复杂度$O(\log n)$——与AVL树相当

• 局部性强、缓存命中率极高时（即k<< n << m）

  • 效率甚至可以更高——自适应的$O(\log k)$
  • 任何连续的m次查找，仅需 时间 $O(m\log k+n\log n)$

• 若反复地顺序访问任一子集，分摊成本仅为常数

• 不能杜绝单次最坏情况，不适用于对效率敏感的场合

二、B-树

1.大数据

1.1 现实A：存储器容量的增长速度 << 应用问题规模的增长速度

• 1990： 10MB / 2MB = 5
• 2020： 10TB / 10GB = 1000
• 相对而言，存储器的容量 实际上在不断减小！

1.2 现实B：在特定工艺及成本下，存储器都是容量与速度的折中产物

• 存储器越大、越快，成本也越高
• 存储器容量越大/小，访问速度越慢/快

1.3 现实C：实用的存储系统，由不同类型的存储器级联而成，以综合其各自的优势

• 不同类型的存储器，容量、访问速度差异悬殊

	#cycles	sec
CPU Register	0	ns
SRAM/cache	4~75	ns
DRAM/main memory	10^2	ns
DISK	10^7	ms

• 若一次内存访问需要一秒，则一次磁盘访问就需一天，为避免一次磁盘访问，我们宁愿访问内存1000次
• 在分级的存储系统中，各类存储器有其各自的角色

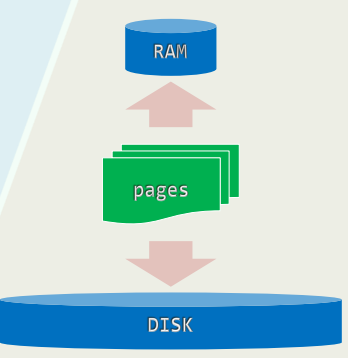
1.4 分级存储：利用数据访问的局部性

• 机制与策略
  • 常用的数据，复制到更高层、更小的存储器中
  • 找不到，才向更低层、更大的存储器索取
• 算法的实际运行时间，主要取决于相邻存储级别之间数据传输（I/O）的速度与次数

1.5 批量访问：在外存读写1B，与读写1KB几乎一样快

• 以页（page）或块（block）为单位，借助缓冲区，可大大缩短单位字节的平均访问时间

#include 
#define BUFSIZ 512 //缓冲区默认容量 
int setvbuf( //定制缓冲区 
    FILE* fp, //流 
    char* buf, //缓冲区 
    int _Mode, //_IOFBF | _IOLBF | _IONBF 
    size_t size //缓冲区容量 
);
int fflush( FILE* fp ); //强制清空缓冲区

2.缓存

2.1 就地循环位移

• 仅用O(1)辅助空间，将数组A[0, n)中的元素向左循环移动k个单元
• void shift( int * A, int n, int k )

2.2 蛮力版

void shift0( int * A, int n, int k ) //反复以1为间距循环左移 { 
    while ( k-- ) shift( A, n, 0, 1 ); 
} //共迭代k次，O(n*k)

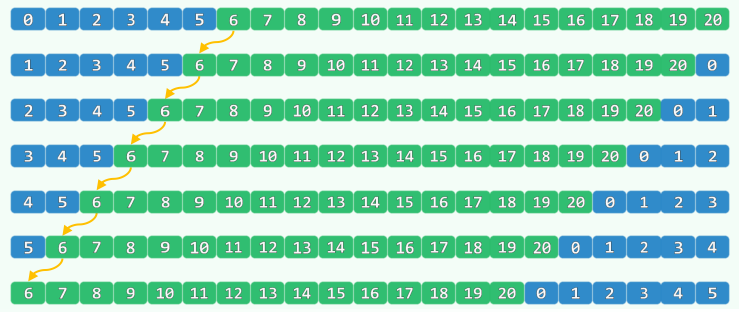
2.3 迭代版

int shift( int * A, int n, int s, int k ) { // O( n / GCD(n, k) ) 
    int b = A[s]; int i = s, j = (s + k) % n; int mov = 0; //mov记录移动次数 
    while ( s != j ) { //从A[s]出发，以k为间隔，依次左移k位 
        A[i] = A[j]; i = j; j = (j + k) % n; mov++; 
    } 
    A[i] = b; return mov + 1; //最后，起始元素转入对应位置 
} //[0, n)由关于k的g = GCD(n, k)个同余类组成，shift(s, k)能够且只能够使其中之一就位

oid shift1(int* A, int n, int k) { //经多轮迭代，实现数组循环左移k位，累计O(n+g) 
    for (int s = 0, mov = 0; mov < n; s++) //O(g) = O(GCD(n, k)) 
        mov += shift(A, n, s, k); 
}

2.4 倒置版

void shift2( int * A, int n, int k ) { 
    reverse( A, k ); //O(3k/2) 
    reverse( A + k, n – k ); //O(3(n-k)/2) 
    reverse( A, n ); //O(3n/2) 
} //O(3n)

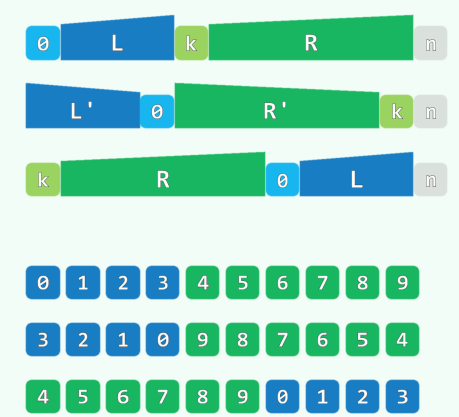
3.结构

3.1 等价变换

• 每d代合并为超级节点
  • m = $2^d$ 路
  • m-1 个关键码
• 逻辑上与BBST完全等价

3.2 I/O优化：多级存储系统中使用B-树，可针对外部查找，大大减少I/O次数

• 对于AVL，若有n = 1G个记录

  • 每次查找需要${\log }_{2}10^9\approx 30$次I/O操作
  • 每次只读出单个关键码，得不偿失

• 对于B-树

  • 充分利用外存的批量访问，将此特点转化为优点
  • 每下降一层，都以超级节点为单位，读入一组关键码

• 具体多大一组视磁盘的数据块大小而定，m = #keys / pg

  • 比如，目前多数数据库系统采用 m = 200~300

• 回到上例，若取m = 256，则每次查找只需${\log }_{256}10^9\le 4$次I/O

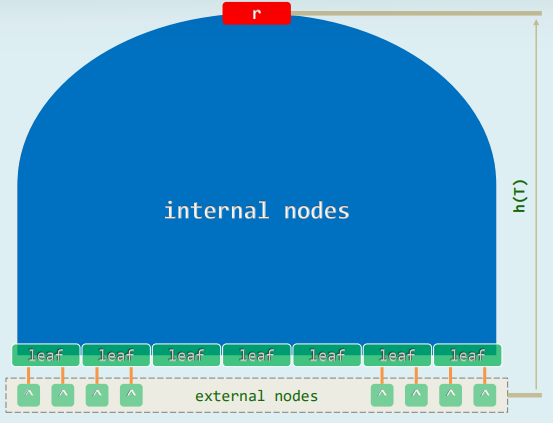
3.3 外部节点 + 叶子

• 所谓m阶B-树，即m路完全平衡搜索树（m ≥3）
• 外部节点的深度统一相等，约定以此深度作为树高h
• 叶节点的深度统一相等（h-1）

3.4 内部节点

• 各含 n ≤ m-1 个关键码： $K_1<K_2<...<K_n$
• 各有n+1≤n个分支：A_0,A_1,…,A_n
• 反过来，分支数也不能太少
  • 树根：2≤n+1
  • 其余： $\lceil m/2\rceil$≤n+1
• 故亦称作($\lceil m/2\rceil ,m$)-树

3.5 紧凑表示

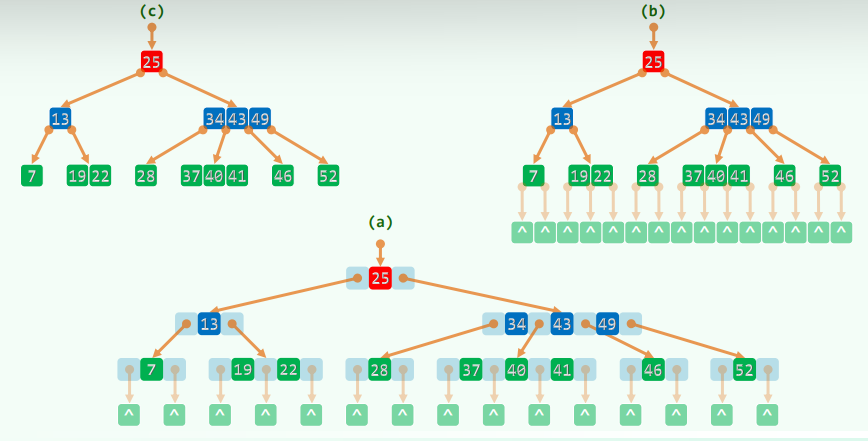
3.6 BTNode

template<typename T> struct BTNode { //B-树节点 
    BTNodePosi<T> parent; 
    Vector<T> key; //关键码（总比孩子少一个）
    Vector< BTNodePosi<T>> child;  
    BTNode() { parent = NULL; child.insert( NULL ); } 
    BTNode( T e, BTNodePosi lc = NULL, BTNodePosi rc = NULL ) { 
        parent = NULL; //作为根节点 
        key.insert( e ); //仅一个关键码，以及 
        child.insert( lc ); if ( lc ) lc->parent = this; //左孩子 
        child.insert( rc ); if ( rc ) rc->parent = this; //右孩子 
    }
};

3.7 BTree

template<typename T> using BTNodePosi = BTNode<T>*; //B-树节点位置 
template<typename T> class BTree {
protected: 
    int _size; int _m; BTNodePosi _root; //关键码总数、阶次、根 
    BTNodePosi<T> _hot; //search()最后访问的非空节点位置 
    void solveOverflow( BTNodePosi ); //因插入而上溢后的分裂处理 
    void solveUnderflow( BTNodePosi ); //因删除而下溢后的合并处理 
public: 
    BTNodePosi<T> search( const T & e ); //查找 
    bool insert( const T & e ); //插入 
    bool remove( const T & e ); //删除 
}

4.查找

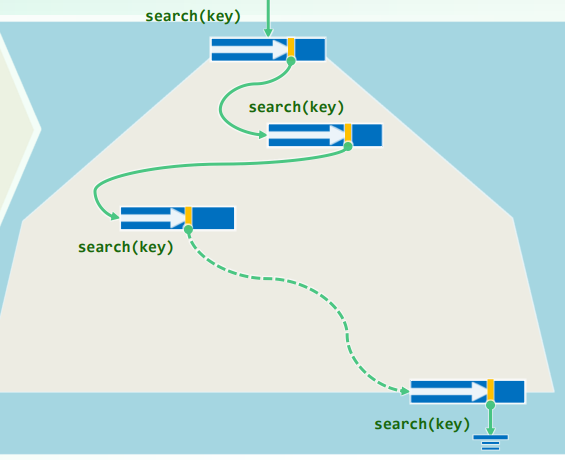
4.1 算法

从（常驻RAM的）根节点开始 
只要当前节点不是外部节点 
    在当前节点中顺序查找 //RAM内部 
    若找到目标关键码，则 
        返回查找成功 
    否则 //止于某一向下的引用 
        沿引用找到孩子节点 
        将其读入内存 //I/O耗时 
返回查找失败

4.2 实现

template<typename T> BTNodePosi<T> BTree<T>::search( const T & e ) { 
    BTNodePosi<T> v = _root; _hot = NULL; //从根节点出发 
    while ( v ) { //逐层深入地 
        Rank r = v->key.search( e ); //在当前节点对应的向量中顺序查找 
        if ( 0 <= r && e == v->key[r] ) return v; //若成功，则返回；否则... 
        _hot = v; v = v->child[ r + 1 ]; //沿引用转至对应的下层子树，并载入其根（I/O） 
    } //若因!v而退出，则意味着抵达外部节点 
    return NULL; //失败 实现
}

4.3 性能

• 约定：根节点常驻RAM
• 忽略内存中的查找，运行时间主要取决于I/O次数
• 在每一深度至多一次I/O
• 故运行时间 = $O(\log n)$
• 可以证明：${\log }_m(N+1)\le h\le 1+\lfloor {\log }_{\lfloor m/2\rfloor }(N+1)/2\rfloor$

4.4 最大树高

• 内部节点应尽可能地“瘦”
  • $n_k\ge 2\cdot \lceil m/2{\rceil }^{k-1},\forall k>0$
• 考查外部节点所在的那层：
  • $N+1=n_k\ge 2\cdot \lceil m/2{\rceil }^{h-1}$
  • $h\le 1+\lfloor {\log }_{\lceil m/2\rceil }(N+1)/2\rfloor =O({\log }_{m}N)$
• 相对于BBST： ${\log }_{\lceil m/2\rceil }(N/2)/{\log }_{2}N=1/({\log }_{2}m-1)$

4.5 最小树高

• 内部节点应尽可能“胖”
  • $n_k\le m^k,\forall k>0$
• 依然，考查外部节点所在的那层
  • $N+1=n_k\le m^h$
  • $h\ge \lceil {\log }_m(N+1)\rceil =\Omega (lo{g}_{m}N)$
• 相对于BBST：$({\log }_{m}N-1)/{\log }_{2}N={\log }_{m}2-{\log }_{N}2\approx 1/{\log }_{2}m$

5.插入

5.1 算法

template<typename T> bool BTree<T>::insert( const T & e ) { 
    BTNodePosi<T> v = search( e ); 
    if ( v ) return false; //确认e不存在 
    Rank r = _hot->key.search( e ); //在节点_hot中确定插入位置
    _hot->key.insert( r+1, e ); //将新关键码插至对应的位置 
    _hot->child.insert( r+2, NULL ); _size++; //创建一个空子树指针 
    solveOverflow( _hot ); //若上溢，则分裂 
    return true; //插入成功 
}

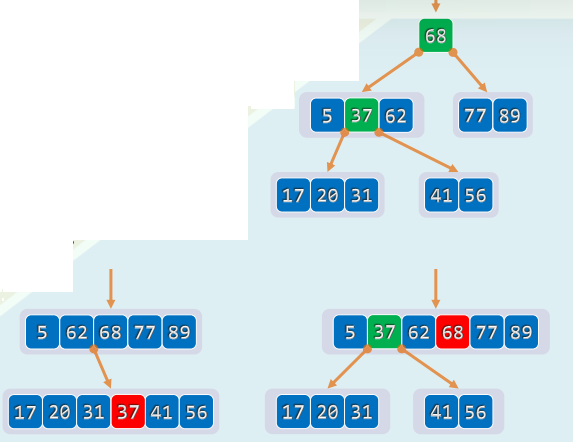
5.2 分裂

• 设上溢节点中的关键码依次为：{$k_0,k_1,...,k_{m-1}$}
• 取中位数$s=\lfloor m/2\rfloor$，以关键码$k_s$为界划分为{$k_0,k_1,...,k_{s-1}$} {$k_s$} {$k_{s+1},...,k_{m-1}$}
• 关键码$k_s$上升一层，并分裂（split） 以所得的两个节点作为左、右孩子

5.3 再分裂

• 若上溢节点的父亲本已饱和，则在接纳被提升的关键码之后，也将上溢，此时，大可套用前法，继续分裂

• 上溢可能持续发生，并逐层向上传播，纵然最坏情况，亦不过到根

• 可令被提升的关键码自成节点，作为新的树根，这是B-树增高的唯一可能

• 注意：新生的树根仅有两个分支

• 总体执行时间正比于 分裂次数，O(h)

5.4 上溢修复

template<typename T> void BTree<T>::solveOverflow( BTNodePosi<T> v ) { 
    while ( _m <= v->key.size() ) { //除非当前节点不再上溢 
        Rank s = _m / 2; //轴点（此时_m = key.size() = child.size() - 1） 
        BTNodePosi u = new BTNode(); //注意：新节点已有一个空孩子 
        for ( Rank j = 0; j < _m - s - 1; j++ ) { //分裂出右侧节点u（效率低可改进）
            u->child.insert( j, v->child.remove( s + 1 ) ); //v右侧_m–s-1个孩子 
            u->key.insert( j, v->key.remove( s + 1 ) ); //v右侧_m–s-1个关键码 
    } 
    u->child[ _m - s - 1 ] = v->child.remove( s + 1 ); //移动v最靠右的孩子 
    if ( u->child[ 0 ] ) //若u的孩子们非空，则统一令其以u为父节点 
        for ( Rank j = 0; j < _m - s; j++ ) u->child[ j ]->parent = u; 
    BTNodePosi<T> p = v->parent; //v当前的父节点p 
    if ( ! p ) //若p为空，则创建之（全树长高一层，新根节点恰好两度） 
        { _root = p = new BTNode(); p->child[0] = v; v->parent = p; } 
    Rank r = 1 + p->key.search( v->key[0] ); //p中指向u的指针的秩 
    p->key.insert( r, v->key.remove( s ) ); //轴点关键码上升 
    p->child.insert( r + 1, u ); u->parent = p; //新节点u与父节点p互联 v = p; //上升一层，如有必要则继续分裂——至多O(logn)层 
    } 
}

6.删除

6.1 算法

template<typename T> 
bool BTree<T>::remove( const T & e ) { 
    BTNodePosi<T> v = search( e ); if ( ! v ) return false; //确认e存在 
    Rank r = v->key.search(e); 
    if ( v->child[0] ) {//若v非叶子，则 
        BTNodePosi<T> u = v->child[r + 1]; //在右子树中 
        while ( u->child[0] ) u = u->child[0]; //一直向左，即可找到e的后继（必在底层） 
        v->key[r] = u->key[0]; v = u; r = 0; //交换
    } 
    //assert: 至此，v必位于最底层，且其中第r个关键码就是待删除者 
    v->key.remove( r ); v->child.remove( r + 1 ); _size--; 
    solveUnderflow( v ); return true; //如有必要，需做旋转或合并 
}

6.2 旋转

• 非根节点 V 下溢时，必恰有$\lceil m/2\rceil -2$个关键码和$\lceil m/2\rceil -1$个分支

• 视其左、右兄弟 L 、 R 的规模，可分三种情况加以处理

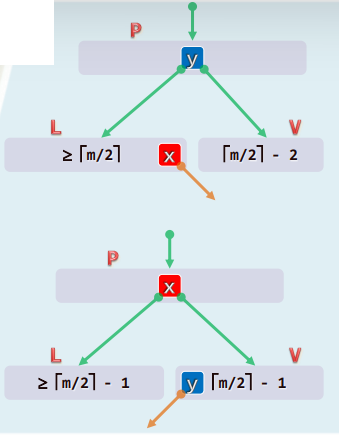
• （1)若 L 存在，且至少包含$\lceil m/2\rceil$个关键码

  • 将 P 中的分界关键码 y 移至 V 中（作为最小关键码）
  • 将 L 中的最大关键码 x 移至 P 中（取代原关键码 y ）

• 如此旋转之后，局部乃至全树都重新满足B-树条件下溢修复完毕

• （2)若 R 存在，且至少包含$\lceil m/2\rceil$个关键码

  • 也可旋转，完全对称

6.3 合并

• (3) L 和 R 或不存在，或均不足$\lceil m/2\rceil$个关键码——即便如此

  • L 和 R 仍必有其一（不妨以 L 为例），且恰含$\lceil m/2\rceil -1$个关键码

• 从 P 中抽出介于 L 和 V 之间的分界关键码 y

  • 通过 y 做粘接，将 L 和 V 合成一个节点
  • 同时合并此前 y 的孩子引用

• 下溢可能持续发生并向上传播；但至多不过 O(h) 层

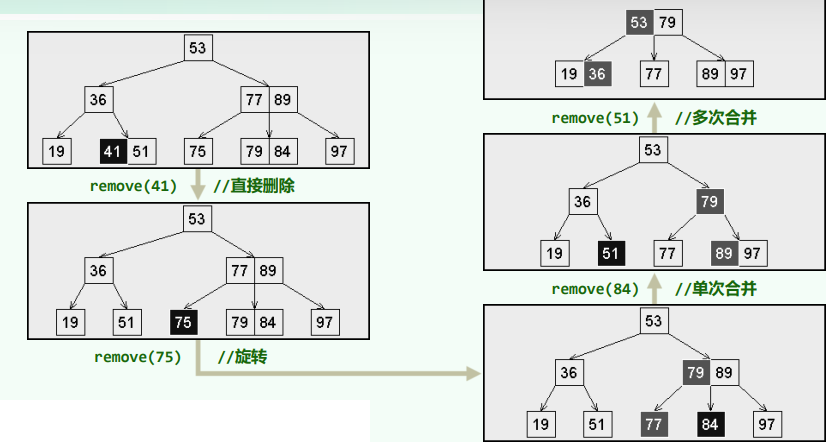
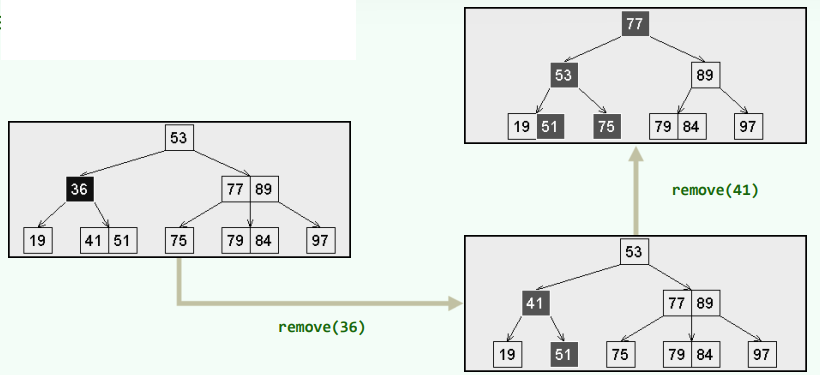
6.4 实例

• 底层节点

• 非底层节点

6.5 下溢修复

template <typename T> void BTree<T>::solveUnderflow( BTNodePosi<T> v ) { 
    while ( (_m + 1) / 2 > v->child.size() ) {//除非当前节点没有下溢 
        BTNodePosi<T> p = v->parent; if ( !p ) { /* 已到根节点 */ } 
        Rank r = 0; while ( p->child[r] != v ) r++; //确定v是p的第r个孩子 
        if ( 0 < r ) { //若v不是p的第一个孩子，则 
        BTNodePosi ls = p->child[r - 1]; //左兄弟必存在 
            if ( (_m + 1) / 2 < ls->child.size() ) { //若该兄弟足够“胖”，则 
                v->key.insert( 0, p->key[r-1] ); //p借出一个关键码给v（作为最小关键码） 
                p->key[r - 1] = ls->key.remove( ls->key.size() – 1 ); //ls的最大key转入p 
                v->child.insert( 0, ls->child.remove( ls->child.size() – 1 ) ); 
                //同时ls的最右侧孩子过继给v（作为v的最左侧孩子） 
                if ( v->child[0] ) v->child[0]->parent = v; return; //至此，通过右旋已完成当前层（以及所有层）的下溢处理 
            } 
        } 
        if ( p−>child.size() − 1 > r ) {/∗若v的右兄弟存在，与上一情况完全对称∗/} 
        if ( 0 < r ) { /∗ 与左兄弟合并 ∗/ 
            BTNodePosi ls = p->child[r-1]; //左兄弟必存在 
            ls->key.insert( ls->key.size(), p->key.remove(r - 1) ); 
            p->child.remove( r ); //p的第r - 1个关键码转入ls，v不再是p的第r个孩子 
            ls->child.insert( ls->child.size(), v->child.remove( 0 ) ); 
            if ( ls->child[ ls->child.size() – 1 ] ) //v的最左侧孩子过继给ls做最右侧孩子 
                ls->child[ ls->child.size() – 1 ]->parent = ls;
            while ( !v->key.empty() ) { //v剩余的关键码和孩子，依次转入ls 
                ls->key.insert( ls->key.size(), v->key.remove(0) ); 
                ls->child.insert( ls->child.size(), v->child.remove(0) ); 
                if ( ls->child[ ls->child.size() – 1 ] ) 
                    ls->child[ ls->child.size() – 1 ]->parent = ls; 
            } 
            release(v); //释放v
        } else { /∗与右兄弟合并，完全对称∗/}
        v = p; //上升一层，如有必要则继续旋转或合并——至多O(logn)层 
    } 
}

三、红黑树

1.动机

1.1 并发性(Concurrent Access To A Database)

• 修改之前先加锁（lock）；完成后解锁（unlock）,访问延迟主要取决于“lock/unlock”周期

• 对于BST而言，每次修改过程中，唯结构有变（reconstruction）处才需加锁,访问延迟主要取决于这类局部之数量

• Splay(伸展树)：结构变化剧烈，最差可达O(n)

• AVL：remove()时$O(\log n)$ ——尽管 insert()时可保证O(1)

• Red-Black：无论insert/remove，均不超过O(1)

1.2 持久性(Persistent structures):支持对历史版本的访问

• 蛮力实现：每个版本独立保存；各版本自成一个搜索结构
• 单次操作$O(\log h+\log n)$，累计O(n·h)时间/空间

1.3 压缩存储：大量共享，少量更新：每个版本的新增复杂度，仅为$O(\log n)$

• 部分持久性(Partial Persistence)：仅支持对历史版本的读取
• 这类情况下，还可进一步提高至总体O（n+h）、单版本O（1）

1.4 O(1)重构

• 为此，就树形结构的拓扑而言，相邻版本之间的差异不能超过O(1)

2.结构

2.1 红与黑

• 由红、黑两类节点组成的BST统一增设外部节点NULL，使之成为真二叉树

2.2 规则

• 树根：必为黑色

• 外部节点：均为黑色

• 红节点：只能有黑孩子（及黑父亲）

• 外部节点：黑深度（黑的真祖先数目）相等

  • 亦即根（全树）的黑高度
  • 子树的黑高度，即后代NULL的相对黑深度

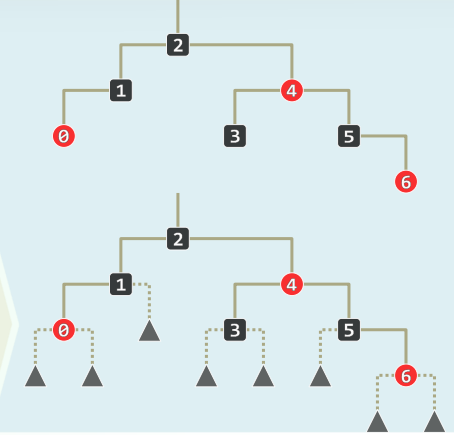
2.3 红黑树 = (2,4)-树

• 将红节点提升至与其（黑）父亲等高——于是每棵红黑树，都对应于一棵(2,4)-树
• 将黑节点与其红孩子视作关键码，再合并为B-树的超级节点
• 无非四种组合，分别对应于4阶B-树的一类内部节点

2.4 红黑树∈BBST

• 包含n个内部节点的红黑树T，高度$h=O(\log n)$（既然B-树是平衡的，由等价性红黑树也应是）
  • ${\log }_2(n+1)\le h\le 2\cdot {\log }_2(n+1)$
• 若T高度为h，红/黑高度为R/H，则$H\le h\le R+H\le 2\cdot H$
• 若T所对应的B-树为$T_B$,则H即是$T_B$的高度
• $T_B的每个节点，都恰好包含T的一个黑节点
• 于是，$H\le {\log }_{\lceil 4/2\rceil }(n+1)/2+1={\log }_2(n+1)$

2.5 RedBlack

template<typename T> class RedBlack : public BST<T> { //红黑树 
public: //BST::search()等其余接口可直接沿用 
    BinNodePosi insert( const T & e ); //插入（重写） 
    bool remove( const T & e ); //删除（重写） 
protected: 
    void solveDoubleRed( BinNodePosi x ); //双红修正 
    void solveDoubleBlack( BinNodePosi x ); //双黑修正 
    int updateHeight( BinNodePosi x ); //更新节点x的高度（重写） 
}; 

template<typename T> int RedBlack<T>::updateHeight( BinNodePosi<T> x ) { 
return x->height = IsBlack( x ) + max( stature( x->lc ), stature( x->rc ) ); 
}

3.插入

3.1 算法

• 按BST规则插入关键码e //x = insert(e)必为叶节点
• 除非系首个节点（根），x的父亲p = x->parent必存在，首先将x染红 //x->color = isRoot(x) ? B : R
• 至此，条件1、2、4依然满足； 但3不见得，有可能双红（double-red）

3.2 实现

template BinNodePosi RedBlack::insert( const T & e ) { 
    // 确认目标节点不存在（留意对_hot的设置） 
    BinNodePosi & x = search( e ); if ( x ) return x; 
    // 创建红节点x，以_hot为父，黑高度 = 0 
    x = new BinNode( e, _hot, NULL, NULL, 0 ); _size++; 
    // 如有必要，需做双红修正，再返回插入的节点 
    BinNodePosi xOld = x; solveDoubleRed( x ); return xOld; 
} //无论原树中是否存有e，返回时总有x->data == e

3.3 u为黑色时

• 此时，x、p、g的四个孩子 （可能是外部节点）全为黑，且黑高度相同

• 局部“3+4”重构，b转黑，a或c转红
• 在某三叉节点中插入红关键码后，原黑关键码不再居中（RRB或BRR）
• 调整的效果，无非是将三个关键码的颜色改为RBR

3.4 u为红色时

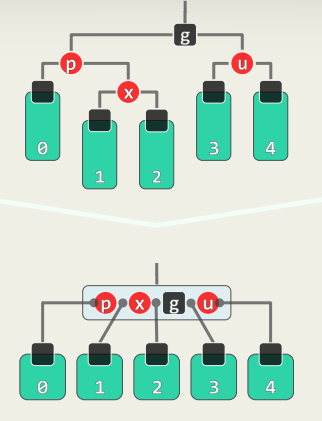
• 在B-树中，等效于超级节点发生上溢

• p与u转黑，g转红，在B-树中，等效于节点分裂，关键码g上升一层

• 既然是分裂，也应有可能继续向上传递——亦即，g与parent(g)再次构成双红

• 果真如此，可等效地将g视作新插入的节点，区分以上两种情况，如法处置

• 直到所有条件满足（即不再双红），或者抵达树根

• g若果真到达树根，则强行将其转为黑色（整树黑高度加一）

3.5 双红修正

template<typename T> void RedBlack<T>::solveDoubleRed( BinNodePosi x ) { 
    if ( IsRoot( *x ) ) { //若已（递归）转至树根，则将其转黑，整树黑高度也随之递增 
        _root->color = RB_BLACK; _root->height++; return; 
    } //否则... 
    BinNodePosi<T> p = x->parent; //考查x的父亲p（必存在） 
    if ( IsBlack( p ) ) return; //若p为黑，则可终止调整；否则 
    BinNodePosi<T> g = p->parent; //x祖父g必存在，且必黑 
    BinNodePosi<T> u = uncle( x ); //以下视叔父u的颜色分别处理 
    if ( IsBlack( u ) ) { //u为黑或NULL 
        // 若x与p同侧，则p由红转黑，x保持红；否则，x由红转黑，p保持红 
        if ( IsLChild( *x ) == IsLChild( *p ) ) p->color = RB_BLACK; 
        else x->color = RB_BLACK; 
        g->color = RB_RED; //g必定由黑转红 
        BinNodePosi<T> gg = g->parent; //great-grand parent 
        BinNodePosi<T> r = FromParentTo( *g ) = rotateAt( x ); 
        r->parent = gg; //调整之后的新子树，需与原曾祖父联接
    } 
    else {/u为红色 
        p->color = RB_BLACK; p->height++; //p由红转黑，增高 
        u->color = RB_BLACK; u->height++; //u由红转黑，增高 
        g->color = RB_RED; //在B-树中g相当于上交给父节点的关键码，故暂标记为红 
        solveDoubleRed( g ); //继续调整：若已至树根，接下来的递归会将g转黑（尾递归）
    }  
}

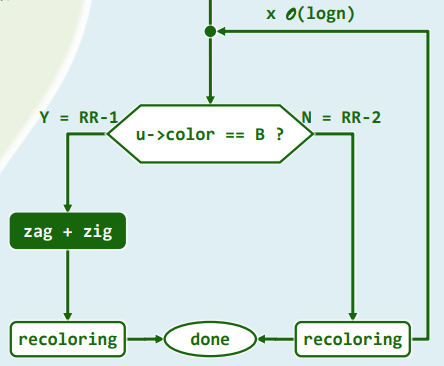
3.6 复杂度

• 重构、染色均只需常数时间，故只需统计其总次数
• RedBlack::insert()仅需$O(\log n)$时间
• 其间至多做$O(\log n)$次重染色、O(1)次旋转

	旋转	染色	此后
u为黑	1~2	2	调整随即完成
u为红	0	3	可能再次双红 但必上升两层

4.删除

4.1 等效删除

• 首先按照BST常规算法，执行r = removeAt( x, _hot ) （实际被摘除的可能是x的前驱或后继w，简捷起见，以下不妨统称作x）

• x由孩子r接替，此时另一孩子k必为NULL

• 但在随后的调整过程中，x可能逐层上升

• 故需假想地、统一地、等效地理解为：

  • k为一棵黑高度与r相等的子树，且随x一并摘除（尽管实际上从未存在过）

4.2 其一为红

• 完成removeAt()之后
  • 条件1、2依然满足
  • 但条件3、4却不见得
• 在原树中，考查x与r
  • 若x为红，则条件3、4自然满足
  • 若r为红，则令其与x交换颜色
• 总之，无论x或r为红，则3、4均不难满足 ——删除遂告完成

4.3 双黑

• 摘除x并代之以r后，全树黑深度不再统一（等效于B-树中x所属节点下溢）

4.4 实现

template<typename T> bool RedBlack<T>::remove( const T & e ) { 
    BinNodePosi<T> & x = search( e ); if ( !x ) return false; //查找定位 
    BinNodePosi<T> r = removeAt( x, _hot ); //删除_hot的某孩子，r指向其接替者 
    if ( ! ( -- _size ) ) return true; //若删除后为空树，可直接返回 
    if ( ! _hot ) { //若被删除的是根，则 
        _root->color = RB_BLACK; //将其置黑，并 
        updateHeight( _root ); //更新（全树）黑高度 
        return true; 
    } //至此，原x（现r）必非根
    // 若父亲（及祖先）依然平衡，则无需调整 
    if ( BlackHeightUpdated( * _hot ) ) return true; 
    // 至此，必失衡 
    // 若替代节点r为红，则只需简单地翻转其颜色 
    if ( IsRed( r ) ) { r->color = RB_BLACK; r->height++; return true; } 
    // 至此，r以及被其替代的x均为黑色 
    solveDoubleBlack( r ); //双黑调整（入口处必有 r == NULL） 
    return true; 
}

4.5 s为黑，且至少有一个红孩子t

• “3+4”重构：

  • t ~ a
  • s ~ b
  • p ~ c

• r保持黑,a、c染黑,b继承p的原色

• 如此，红黑树性质在全局得以恢复——删除完成

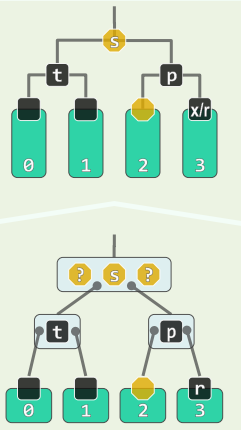
• 通过关键码的旋转,消除超级节点的下溢
• 在对应的B-树中
  • p若为红,问号之一为黑关键码
  • p若为黑,必自成一个超级节点

4.6 s为黑，且两个孩子均为黑

• p为红

  • r保持黑；s转红；p转黑

  • 在对应的B-树中，等效于下溢节点与兄弟合并

  • 红黑树性质在全局得以恢复

  • 失去关键码p后，上层节点不会继而下溢

  • 合并之前，在p之左或右侧 还应有一个黑关键码

• p为黑

  • s转红；r与p保持黑

  • 红黑树性质在局部得以恢复

  • 在对应的B-树中，等效于下溢节点与兄弟合并

  • 合并前，p和s均属于单关键码节点 （孩子的下溢修复后，父节点继而下溢）

  • 好在可继续分情况处理高度递增，至多$O(\log n)$层（步）

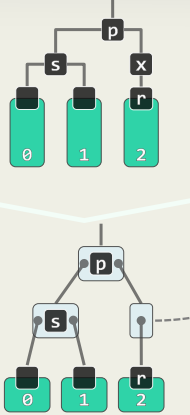
4.7 s为红（其孩子均为黑）

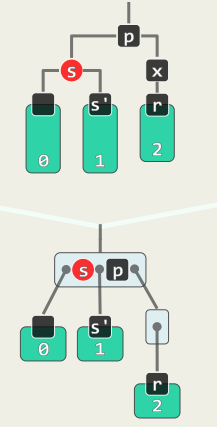
• 绕p单旋；s红转黑，p黑转红

• 黑高度依然异常

• 但r有了一个新的黑兄弟s’ 故转化为前述情况

• 既然p已转红，接下来绝不会是BB-2B,而只能是BB-2R或BB-1

• 于是，再经一轮调整,红黑树性质必然全局恢复

4.8 双黑修正

template<typename T> void RedBlack<T>::solveDoubleBlack( BinNodePosi r ) { 
    BinNodePosi<T> p = r ? r->parent : _hot; if ( !p ) return; //r的父亲 
    BinNodePosi<T> s = (r == p->lc) ? p->rc : p->lc; //r的兄弟 
    if ( IsBlack( s ) ) { //兄弟s为黑 
        BinNodePosi t = NULL; //s的红孩子（若左、右孩子皆红，左者优先；皆黑时为NULL） 
        if ( IsRed ( s->rc ) ) t = s->rc; 
        if ( IsRed ( s->lc ) ) t = s->lc; 
        if ( t ) { /* ... 黑s有红孩子*/ 
            RBColor oldColor = p->color; //备份p颜色，并对t、父亲、祖父 
            BinNodePosi<T> b = FromParentTo( *p ) = rotateAt( t ); //旋转 
            if (HasLChild( *b )) { b->lc->color = RB_BLACK; updateHeight( b->lc ); } 
            if (HasRChild( *b )) { b->rc->color = RB_BLACK; updateHeight( b->rc ); } 
            b->color = oldColor; updateHeight( b ); //新根继承原根的颜色
        } 
        else { /* ... 黑s无红孩子*/ 
            s->color = RB_RED; s->height--; //s转红 
            if ( IsRed( p ) ) //p转黑，但黑高度不变 
                { p->color = RB_BLACK; } 
            else //p保持黑，但黑高度下降；递归修正 
                { p->height--; solveDoubleBlack( p ); }
        } 
    } else { /* ... 兄弟s为红*/ 
        s->color = RB_BLACK; p->color = RB_RED; //s转黑，p转红 
        BinNodePosi<T> t = IsLChild( *s ) ? s->lc : s->rc; //取t与其父s同侧 
        _hot = p; FromParentTo( *p ) = rotateAt( t ); //对t及其父亲、祖父做平衡调整 
        solveDoubleBlack( r ); //继续修正r——此时p已转红，故后续只能是第一种或第二种
    }
}

4.9 复杂度

• RedBlack::remove() 仅需$O(\log n)$时间
  • $O(\log n)$次重染色
  • $O(1)$次旋转

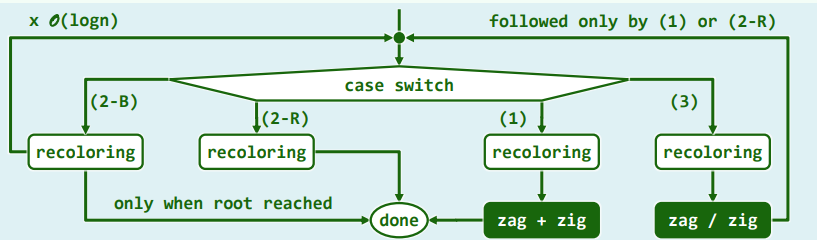
	旋转	染色	此后
黑s有红子t	1~2	3	调整随即完成
黑s无红子，p红	0	2	调整随即完成
黑s无红子，p黑	0	1	必再次双黑，但将上升一层
红s	1	2	转为(1)或(2R)