数据结构（c++）学习笔记--串

---

一、ADT

1.术语

• 相等：S[0,n)=T[0,m)

  • 长度相等（n=m），且对应的字符均相等（S[i]=T[i]）

• 字串：S.substr(i,k)=S[i,i+k),0≤i<n,0≤k

  • 亦即，从S[i]起的连续k个字符

• 前缀：S.prefix(k)=S.substr(0,k)=S[0,k),0≤k≤n
  • 亦即，S中最靠前的k个字符

• 后缀：S.suffix(k)=S.substr(n-k,k)=S[n-k,n),0≤k≤n
  • 亦即，S中最靠后的k个字符

• 联系：S.substr(i,k)=S.prefix(i+k)

• 空串：S[0,n=0)，也是任何串的子串，前缀，后缀

• 长度严格小于原串的子串，前缀，后缀也称作真子串，真前缀，真后缀

2.ADT

ADT	图例
length()
charAt(i)
substr(i, k)
prefix(k)
suffix(k)
concat(T)
equal(T)
indexOf§

二、模式匹配：问题 & 蛮力算法

1.串匹配

• %grep<pattern><text>

  • 文本T=now is the time for all good $\underline{\text{people}}$ to come
  • 模式P=people

• 记n=|T|和m=|P|,通常有n>>m>>2

• 模式匹配（Pattern matching）

  • detection:P是否出现
  • location:首次在哪里出现
  • counting:共有几次出现
  • enumeration:各出现在哪里

2.蛮力匹配

2.1 构思

• 自左向右，以字符为单位，依次移动模式串，直到在某个位置，发现匹配

2.2 两种实现

int match( char * P, char * T ) { 
    size_t n = strlen(T), i = 0; 
    size_t m = strlen(P), j = 0; 
    while ( j < m && i < n ) //自左向右逐次比对 
        if ( T[i] == P[j] ) { i ++; j ++; } //若匹配，则转到下一对字符 
        else { i -= j-1; j = 0; } //否则，T回退、P复位 
    return i-j; //最终的对齐位置：藉此足以判断匹配结果
}

int match( char * P, char * T ) { 
    size_t n = strlen(T), i = 0; 
    size_t m = strlen(P), j; 
    for ( i = 0; i < n-m+1; i ++ ) { //T[i]与P[0]对齐后 
        for ( j = 0; j < m; j ++ ) //逐次比对 
            if ( T[i+j] != P[j] ) break; //失配，转下一对齐位置 
        if ( m <= j ) break; //完全匹配 
    } 
    return i; //最终的对齐位置：藉此足以判断匹配结果
}

2.3 复杂度

• 最好情况（只经过一轮比对，即可确定匹配）：#比对=m=O(m)

• 最坏情况（每轮都比对至P的末字符，且反复如此）

  • 每轮循环：#比对=m-1（成功）+1（失败）=m
  • 循环次数=n-m+1
  • 一般地有m<<n，故总体地，#比对=m·(n-m+1)=O(n·m)

• $|\sum |$越小，最坏情况出现的概率越高

• m越大，最坏情况的后果更加严重

三、KMP算法

1.记忆法

1.1 低效~局部匹配

• 最好情况：O(n)
• 最坏情况：O(n·m)

1.2 不变性

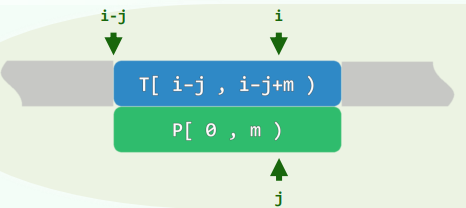
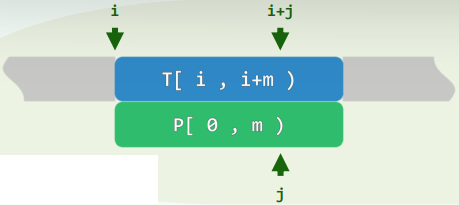
• 在任一时刻，都有 T[ i-j, i ) == P[ 0, j )
• 亦即，我们业已掌握T[i-j,i)的所有信息,既如此一旦失败，我们就应已知 哪些位置值得/不必对齐,而且在下一轮比对中T[i−j’,i)可径直接受，而不必再做比对

• 如此， i将永远不必回退！

  • 比对成功，则与j同步前进一个字符
  • 否则，j更新为某更小的t，并继续比对

• 即便是更为复杂的情况，依然可行

• 优化 = P可快速右移 + 避免重复比对

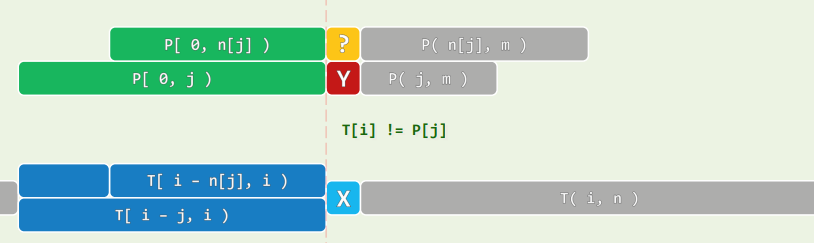
2.查询表

2.1 t：不仅可以事先确定，而且仅根据P[0,j) = T[i-j,i)即可确定

• 视失败的位置j，无非m种情况
• 构造查询表next[0,m)，做好预案
• 一旦在P[j]处失配，只需将j替换为next[j]，继续与T[i]比对

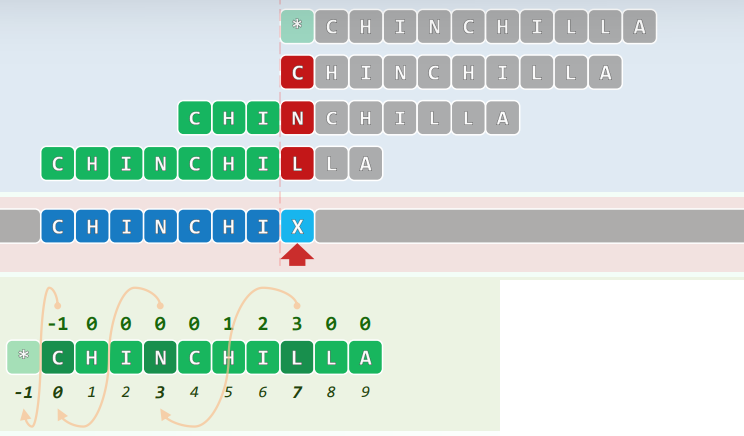
2.2 实例

2.3 KMP算法

int match( char * P, char * T ) { 
    int * next = buildNext(P); 
    int n = (int) strlen(T), i = 0; 
    int m = (int) strlen(P), j = 0; 
    while ( j < m && i < n ) 
        if ( 0 > j || T[i] == P[j] ) { 
            i ++; j ++; 
        } else j = next[j]; 
    delete [] next; 
    return i - j; 
}

3.理解next[]表

3.1 最长自匹配：快速右移 + 绝不回退

• 对任意j，考察集合：N（P,j）={0≤t<j | P[0,t]==P[j-t,j]}

  • 亦即，在P[j]的前缀P[0,j]中，所有匹配真前缀和真后缀的长度

• 因此，一旦T[i]≠P[j],可从N(P,j)中取某个t,令P[t]对准T[i],并继续比对

  • next[j]=max{N(P,j)} -> 长度最大，位移最小，不致日后回溯

3.2 自匹配：传递链

• $next[0]\equiv -1$ -> 假想的哨兵，所有传递链的终点；思考的基础，计算的起点

4.构造next[]表

4.1 递推

• 所谓next(j),即是在P[0,j)中，最大自匹配的真前缀和真后缀的长度
• 故：next[j+1]≤next[j]+1
  • 特别地，当且仅当P[j]==P[next[j]]时取等号

• next[j+1]的候选者，依次应该是1+next[j]、1+next[next[j]]、1+next[next[next[j]]]、…
• 这个序列严格递减，且必收敛于$1+next[0]\equiv 0$

4.2 实例

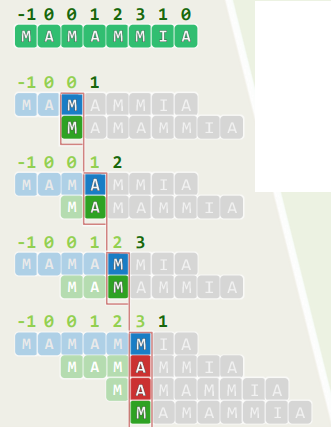
4.3 算法

int * buildNext( char * P ) { 
    size_t m = strlen(P), j = 0; 
    int *N = new int[m]; 
    int t = N[0] = -1; 
    while ( j < m - 1 ) ( 0 > t || P[j] == P[t] ) ? N[ ++j ] = ++t : t = N[t]; 
    return N; 
}

5.分摊分析

• 令：k = 2*i - j

while ( j < m && i < n ) //k必随迭代而单调递增，故也是迭代步数的上界 
    if ( 0 > j || T[i] == P[j] ) 
        { i ++; j ++; } //k恰好加1 
    else 
        j = next[j]; //k至少加1 

• 初始：k = 0，算法结束时：k = 2*i - j ≤2(n - 1) - (-1) = 2n - 1=O(n)

6.再改进

6.1 反例

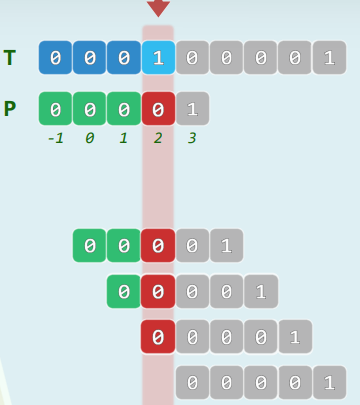
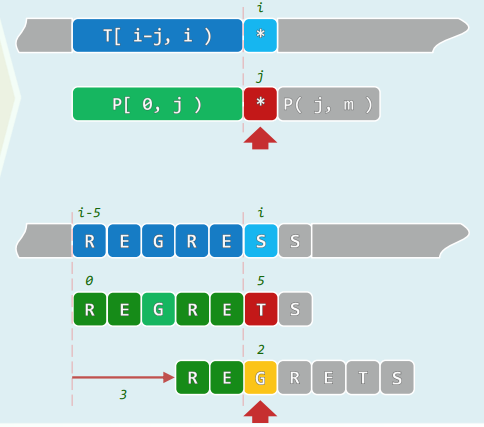
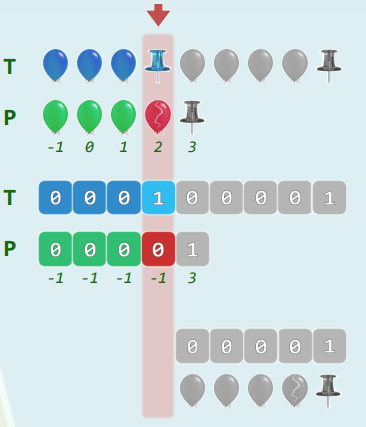
• 在T[3]处 与 P[3] 比对，失败；与 P[2] = P[next[3]] 比对，失败 ；与 P[1] = P[next[2]] 比对，失败；与 P[0] = P[next[1]] 比对，失败。 最终，才前进到T[4]

6.2 根源

• 无需T串，即可在事先确定： P[3] = P[2] = P[1] = P[0] = 0
• 既然如此在发现 T[3] != P[3] 之后，没必要一错再错

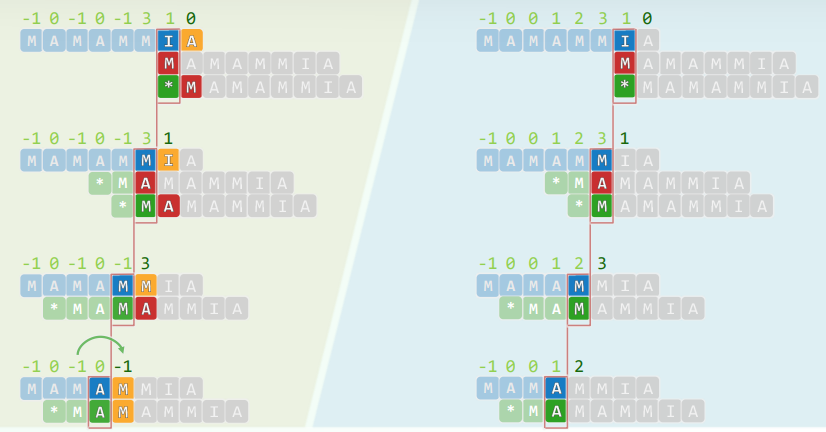
6.3 改进

int * buildNext( char * P ) { 
    size_t m = strlen(P), j = 0; 
    int * N = new int[m]; 
    int t = N[0] = -1; 
    while ( j < m – 1 ) 
        if ( 0 > t || P[j] == P[t] ) { 
            j ++; t ++; 
            N[j] = ( P[j] != P[t] ) ? t : N[t]; 
        } else t = N[t]; return N; 改进 
}

6.4 比对

6.5 小结

• 充分利用以往的比对所提供的信息，模式串快速右移，文本串无需回退

• 经验 ~ 以往成功的比对：T[i-j, i)是什么

• 教训 ~ 以往失败的比对：T[i]不是什么

• 特别适用于顺序存储介质

• 单次匹配概率越大（字符集越小），优势越明显（比如二进制串），否则，与蛮力算法的性能相差无几

四、BM算法：BC策略

1.以终为始

1.1 善待教训，尽早试错

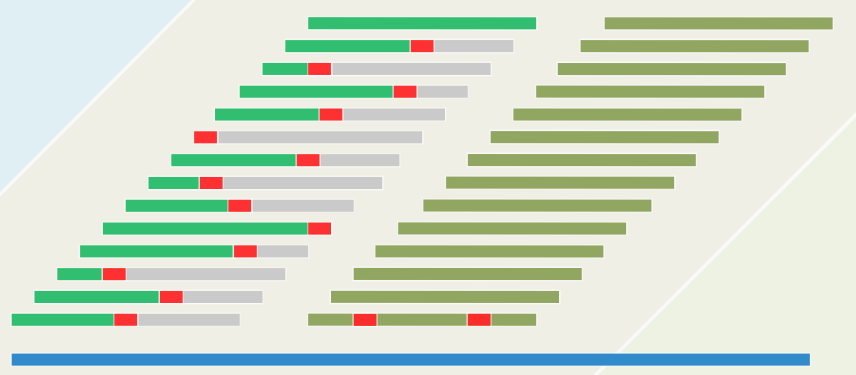
1.2 以终为始

• 既如此，每一趟比对都更应该从末字符开始，自后向前，自右向左
• 4 + 4 < 12

2.坏字符

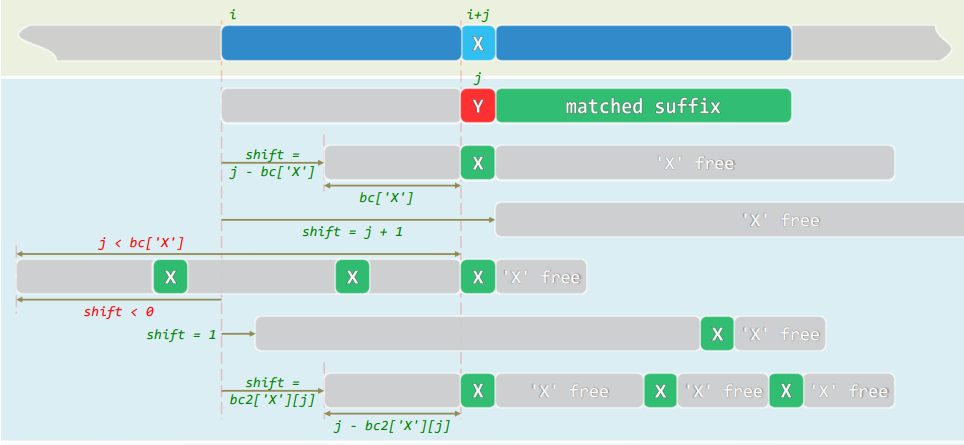
• 某躺扫描中，一旦发现T[i+j]=X≠Y=P[j] -> Y称作坏字符

  • 则P相应地右移，并开启新的一轮扫描比对

• 位移量取决于失配位置j，亦即X在P中的秩，而与T和i无关

• 若令bc[X]=rank[X]=j-shift,则bc[]总计有$s=|\sum |$项，且可事先计算，并制表待查

3.构造bc[]

int * buildBC( char * P ) { 
    int * bc = new int[ 256 ]; //bc[]表，与字母表等长
    for ( size_t j = 0; j < 256; j++ ) bc[j] = -1; //初始化（统一指向通配符）
    for ( size_t m = strlen(P), j = 0; j < m; j++ )//自左向右扫描 
        bc[ P[ j ] ] = j; //刷新P[j]的出现位置记录（画家算法:后来覆盖过往）
    return bc; 
}//第二个循环，通过引入临时变量m，避免反复调用strlen()

• 附加空间$=|bc[]|=O(|\sum |)=O(S)$
• 时间$=O(|\sum |+m)=O(S+m)$

4.性能分析

4.1 最好情况

• O(n/m)

• 一般地

  • 只要P不含T[i+j]，即可直接移动m个字符
  • 仅需单次比较，即可排除m个对齐位置

• 单次匹配概率越小，性能优势越明显

• P越长，这类移动的效果越明显

4.2 最坏情况

• O(n·m)

• 每轮迭代，都要在扫过整个P之后，方能确定右移一个字符
• 此时，须经m次比较，方能排除单个对齐位置
• 单次匹配概率越大的场合，性能越接近于蛮力算法

五、BM算法：GS策略

1.好后缀(Good-Suffix)

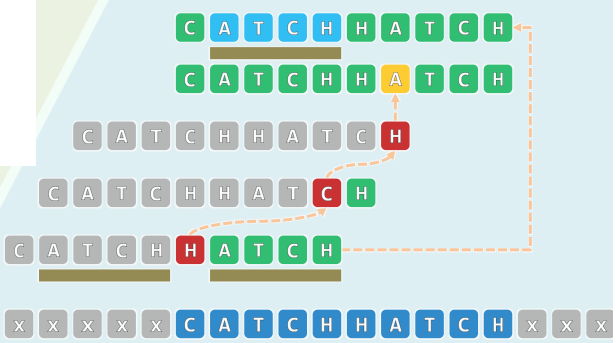
1.1 经验 = 匹配的后缀

• 首趟比对虽失败，却积累了足够的经验（匹配的后缀 ATCH ） //好后缀
• 据此，可省去中间两趟，而直接转至最后一趟（P右移5个字符）
• 这一规律与技巧与KMP如出一辙，只不过前后颠倒而已

1.2 策略

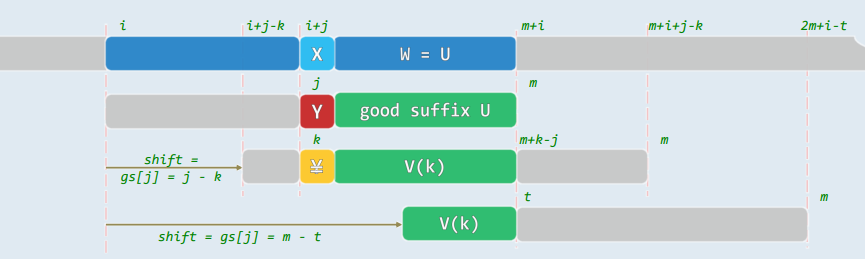
• 扫描比对中断于T[i + j] = X≠Y = P[j]时，U = P(j,m)必为好后缀
• 故下一对齐位置必须使:
  • U重新与V(k) = P( k, m + k - j )匹配，且（经验）
  • P[k] = Y ≠ Y = P[j] （教训）

1.3 完美匹配

• 若P中的确存在这样的子串V(k)，则可选择其中k最大者（尽可能靠后），然后通过右移使之与U对齐（移动距离尽可能小）

1.4 部分匹配

• 否则，在所有前缀P[0,t)中，取与U的后缀匹配的最长者 //注意：有可能t = 0
• 无论如何，位移量仅取决于j和P本身——亦可预先计算，并制表待查

1.5 实例

2.构造gs表

2.1 MS[] -> ss[]

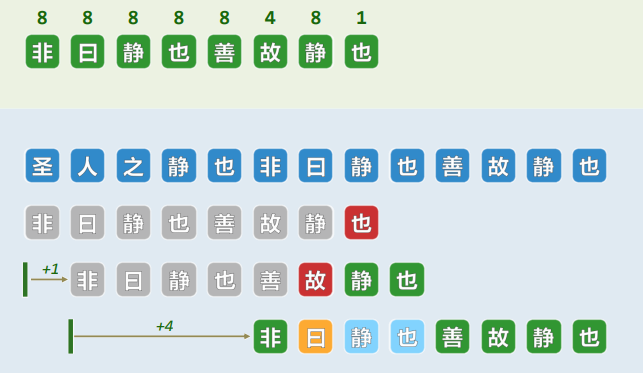
• 对任一0≤j<m，令：ss[j]=max{0≤s≤j+1 | P(j-s,s]=P[m-s,m)}
• 于是，MS[j]=P(j-ss[j],j]就是P[0,j]所有后缀中，与P的某一后缀匹配的最长者

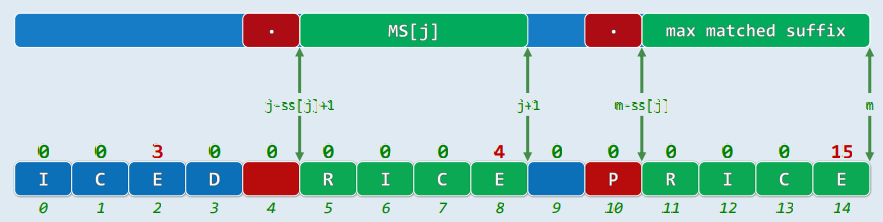
• 实际上，ss[]表中蕴含了gs[]表的所有信息

2.2 ss[] -> gs[]

• (a)若ss[j]=j+1，则对于任何i<m-j-1，m-j-1必是gs[i]的一个候选

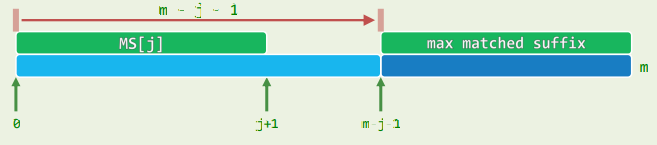
• (b)若ss[j]=j+1，则m-j-1必是gs[m-ss[j]-1]的一个候选

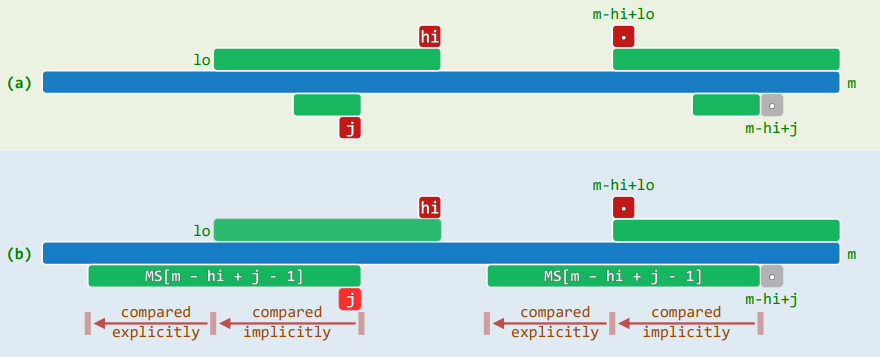
2.3 构造ss[]

• 蛮力地对每个字符都扫描一趟，累计$O(m^2)$；自后向前逆向扫描，只需$O(m)$时间

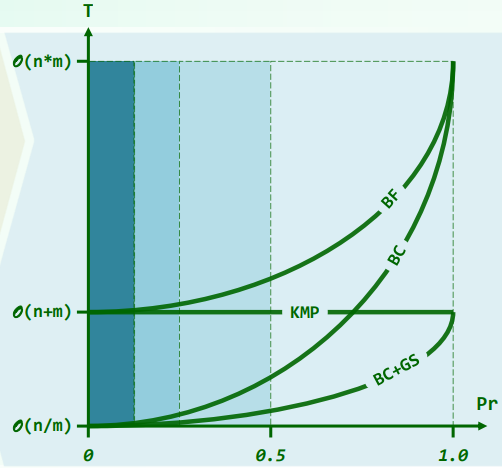
3.综合性能

• 空间 $=|bc|+|gs|=O(|\sum |+m)$
• 预处理：$O(|\sum |+m)$
• 查找效率
  • 最好 O(n / m)
  • 最差 O(n + m)
• 关键因素
  • 单次比对成功的概率
  • 通常，Pr = 1/s

六、Karp-Rabin算法

1.串即是数

1.1 凡物皆数：Gödel Numbering

• 逻辑系统的符号、表达式、公式、命题、定理、公理等，均可表示为自然数
• 每个有限维的自然数向量（包括字符串），都唯一对应于某个自然数
• 素数序列：p(k) = 第k个素数 = 2, 3, 5, 7, 11, 13, 17, 19, …

• $"godel"=2^{1+7}\cdot 3^{1+15}\cdot 5^{1+4}\cdot 7^{1+5}\cdot 11^{1+12}=139869560310664817087943919200000$

1.2 凡物皆数：Cantor Numbering

• $canto{r}_2(i,j)=[(i+j{)}^2+3i+j]/2$

• 长度有限的字符串，都可视作$d=1+|\sum |$进制的自然数
  • $"decade"=453145_{(10)}$
• 长度无限的字符串，都可视作[0,1)内的d进制小数
  • $"bgahbhahbhdei..."=\mathrm{0.2718281828459...}$

1.3 串亦为数

• 十进制串，可直接视作自然数 //指纹（fingerprint），等效于多项式法
  • P = “82818” T = 271 82818 284590452353602874713527
• 一般地，随意对字符编号{ 0, 1, 2, …, d - 1 } (设d = |∑|)，于是每个字符串都对应于一个 d 进制自然数 (尽管不是单射)
  • $"CAT"=2019_{(26)}=1371_{(10)}$ //∑ = { A, B, C, …, Z }
  • $"ABBA"=0110_{(26)}=702_{(10)}$
• P在T中出现 仅当 T中某一子串与P相等

2.散列

2.1 数位溢出

• 如果|∑|很大，模式串P较长，其对应的指纹将很长
  • 比如，若将P视作|P|位的|∑|进制自然数，并将其作为指纹
• 仍以ASCII字符集为例（|∑| = 128 = 27），只要|P| > 9，则指纹的长度将至少是：7 x 10 = 70 bits
• 然而，目前的字长一般也不过64位 //存储不便
• 而更重要地，指纹的计算与比对，将不能在O(1)时间内完成，准确地说，需要O(|P|/64) = O(m)时间；总体需要O(n*m)时间 //与蛮力算法相当

2.2 散列压缩

• 基本构思：通过对比经压缩之后的指纹，确定匹配位置
• 关键技巧：通过散列，将指纹压缩至存储器支持的范围
  • 比如，采用模余函数：hash( key ) = key % 97

2.3 散列冲突

• 注意：hash()值相等，并非匹配的充分条件，因此，通过hash()筛选之后，还须经过严格的比对，方可最终确定是否匹配

• 既然是散列压缩，指纹冲突就在所难免——好在，适当选取散列函数，极大降低冲突的概率

2.4 快速指纹计算

• hash()的计算，似乎每次均需O(|P|)时间
• 观察相邻的两次散列之间，存在某种相关性，相邻的两个指纹之间，也有某种相关性
• 利用上述性质，即可在O(1)时间内，由上一指纹得到下一指纹